分数除法综合练习课课件
合集下载
《分数除以分数》课件

提高练习题
复杂分数的计算
01
提供一些较为复杂的分数除法题目,如带分数、小数、分母较
大等,提高学生的计算能力和对复杂分数的处理能力。
分数除法的变形技巧
02
介绍一些分数除法的变形技巧,如利用倒数性质简化计算、将
除法转化为乘法等,帮助学生提高解题效率。
分数除法与其他数学知识的综合运用
03
结合其他数学知识,如乘法、加减法、比例等,设计一些综合
=
4$,表示$frac{2}{3}$是
$frac{1}{2}$的4倍。
分数除以分数的计算方法
计算方法
将除法转化为乘法,即用一个分 数去除以另一个分数等于将第一 个分数乘以第二个分数的倒数。
例如
$frac{2}{3} div frac{1}{2} = frac{2}{3} times frac{2}{1} = frac{4}{3}$
02
分数除以分数的性质
分数除以分数的商的性质
分数除以分数的商仍为分数
当一个分数除以另一个分数时,其结果仍为一个分数。
商的分子分母变化规律
被除数的分子除以除数的分子,被除数的分母除以除数的 分母,得到的结果即为商。
商的符号判断
如果被除数大于除数,商为正;如果被除数小于除数,商 为负;如果被除数等于除数,商为1。
要求学生熟练掌握分数除以分数的计 算方法和步骤,能够灵活运用解决实 际问题。
要求学生能够通过自主学习和合作学 习,解决复杂数学问题和生活中的实 际问题。
要求学生能够理解和应用分数除以分 数的定义和意义,深入理解其本质。
谢谢您的聆听
THANKS
分数除法在数学中还可以用于证明一些定理和性质,如等差数列的性质、等比数列 的性质等。
六年级数学上册教学课件《分数除法-练习九》

解:设正桥的长度是 x m。 257
x + 578 x = 1670 x = 1156
1670 − 1156 = 514(米)
答:这座大桥的正桥长度是 1156 m,引桥的长度是 514 m。
5 中国二十四节气中的“夏至”是一年中白昼最长、黑夜
最短的一天。这一天,北京的黑夜时长是白昼时长的
3 5
。
是( B )
A.
1 10
+
1 15
B.
1÷(
1 10
+
1 15
)
C.
1÷(1÷
1 10
+1÷
1 15
)
变式训练
(2)一个游泳池可装水360吨,单开进水管20小时注满水池, 单开出水管30小时可把满池水放完,现在同时打开两
管,几小时可把水池注满?正确列式是( C )。
A. 360÷20+360÷30 C.1÷(210-310)
你知道吗?
例如,ba ÷c =
b a
÷
aac=
b ac
(a、c
不等于
0)。如果被除数和除数
都是分数,要先将它们化成同分母的分数。例如,ba ÷
d c
=
bc ac
÷aadc = abdc(a、c、d 不等于 0)。
变式训练
1.选择。
(1)加工一批服装,甲组单独做每天完成110 ,乙组单独 做每天完成115,两组同时加工多少天完成?正确列式
8 某水库准备打开泄洪口调节水位。
只打开 A 口,8小时可以完成任务; 只打开 B 口,6 小时可以完成任务。 如果两个泄洪口同时打开,几小时 可以完成任务?
1÷(
1 8
x + 578 x = 1670 x = 1156
1670 − 1156 = 514(米)
答:这座大桥的正桥长度是 1156 m,引桥的长度是 514 m。
5 中国二十四节气中的“夏至”是一年中白昼最长、黑夜
最短的一天。这一天,北京的黑夜时长是白昼时长的
3 5
。
是( B )
A.
1 10
+
1 15
B.
1÷(
1 10
+
1 15
)
C.
1÷(1÷
1 10
+1÷
1 15
)
变式训练
(2)一个游泳池可装水360吨,单开进水管20小时注满水池, 单开出水管30小时可把满池水放完,现在同时打开两
管,几小时可把水池注满?正确列式是( C )。
A. 360÷20+360÷30 C.1÷(210-310)
你知道吗?
例如,ba ÷c =
b a
÷
aac=
b ac
(a、c
不等于
0)。如果被除数和除数
都是分数,要先将它们化成同分母的分数。例如,ba ÷
d c
=
bc ac
÷aadc = abdc(a、c、d 不等于 0)。
变式训练
1.选择。
(1)加工一批服装,甲组单独做每天完成110 ,乙组单独 做每天完成115,两组同时加工多少天完成?正确列式
8 某水库准备打开泄洪口调节水位。
只打开 A 口,8小时可以完成任务; 只打开 B 口,6 小时可以完成任务。 如果两个泄洪口同时打开,几小时 可以完成任务?
1÷(
1 8
3.2.7 人教《版六年级数学上册第三单元分数除法《练习八》教学课件

(1
−
2 7
)平均每车运走这批大米的114 ,剩下的大米 还要 10 车才能运完。
10 有一组互相咬合的齿轮。
(1)大齿轮有140个齿,小齿轮的齿数是大齿轮的15。小齿轮 有多少个齿? 140× 1 =28(个) 单位“1”已知,用乘法计算。 5 答:小齿轮有28个。
10 有一组互相咬合的齿轮。
5 计算下面各题。
38÷6
=
38×16
=
1 16
3÷15 = 3×5 = 15
10 21
÷
5 7
=
1201×75
=
2 3
194÷3
=
194×13
=
3 14
18÷1123
=
18×1132
=
39 2
15 16
÷
5 8
=
1156×85
=
3 2
26÷
13 25
÷
15 22
=
26×
25 13
×
22 15
=
4 图书馆有科普读物320本,占全部图书的25。科普读物的数
量是故事书的43。 (1)图书馆共有多少本图书?
320÷25=800(本) 答:图书馆共有800本图书。
4 图书馆有科普读物320本,占全部图书的25。科普读物的数
量是故事书的43。 (2)图书馆有多少本故事书?
320÷43=240(本) 答:图书馆有240本故事书。
水的质量少110。现有一块重 9 kg 的冰,如果一桶
水的体积和这块冰的体积相等,这桶水有多重?
9÷(1
−
1 10
)
=
9×
10 9
= 10(kg)
六年级上册数学课件- 3.2 分数除法-人教(共56张PPT)

是爸爸体重的几分之几? ?千克
小明:
15 x=35× 15
35千克
7
x=75
问题:①你们能借助线段图理解这个等量关系式和方程的意思吗?
②图中哪部分是小明体重比爸爸轻的部分?
③他是怎样求小明体重比爸爸轻的部分的?
一、引入情境,探究新知
(二)分析与解答
预设2: 爸爸:
爸爸的体重×(1- 8 )=小明的体重
15
“1”
小明的体重比爸爸轻 8 15
解:设爸爸的体重为x kg。
(1- 8 )x=35
7
15
x=35
是爸爸体重的几分之几? ?千克
小明:
35千克
15 x=35× 15
7
x=75
问题: ①你们能借助线段图理解这个数量关系式和方程的意思吗? ②图中小明的体重相当于爸爸体重的哪一部分? ③小明的体重相当于爸爸体重的几分之几?你是怎样得到的?
(二)自主操作,深入理解
把一张纸的 4 平均分成3份,每份是这张纸的几分之几?
5
预设1: 4 ÷3=
5
4÷3 =?
5
预设2: 4 ÷3=
5
4 ×
5
1 = 3
4 15
4
问题:1.借助手中的学具,折一折,画一画,表示出 5 ÷3 的意义。 2.用算式表示出刚才折或画的过程。
3.结合画好的图,说说你的计算过程。 (出示预设1时)你遇到了什么问题?(出示预设2)说说你的想法。
75 ×(1- 8 )=35
15
预设2:
8
看看小明的体重是不是比爸爸轻 15 (75-35 )÷75 = 8
15
二、巩固练习,提升认识
1.
最新人教版六年级上册数学第三章《分数除法》精品教学课件及课后练习讲解(163页)

方
法
二
=×
= (g) 答:一个成年人一天大约需要 g钙质。
看图列方程计算
36分钟 一场足球赛共x分钟
课堂小结
这节课你们都学会了哪些知识?
已知一个数的几分之几是多少,求这个数的实际问题 解题的方法可以用方程法,也可以用算术法。用算术 法解答时,用除法计算。用方程法解答的步骤:①找出
单位“1”,设为x。②找出数量关系。③列方程解答。
1 分钟=60 秒 60÷ 1 =60×25=1500(个)
25
答:一分钟可以检测1500 个瓶子。
照这个速度,老爷爷每天慢跑要用 多少时间?
半圈就是 21圈; 半圈用2分钟,那么一圈用4分钟。
方法1:6÷ 1=12(个)
2
2×12=24(分)
方法2:2÷ 1=4(分)
2
4×6=24(分)
答:老爷爷每天慢跑要用24 分。
课堂小结
这节课你们都学会了哪些知识?
分数除法的计算方法 除以一个不为0的数,等于乘上这个数 的倒数。
除法转化乘法。
人教版 数学 六年级 上册
3 分数除法
分数混合运算
情境导入
探究新知
课堂练习
课堂小结
课后作业
情境导入 说出运算顺序,不用计算。
100+30÷5 除法 加法 (29+7)×4 加法 乘法
3 分数除法
练习七
复习旧知 课堂小结
巩固练习 课后作业
复习旧知 分数除法的计算法则
除以一个不等于0的数,等于乘这个数的倒数。
小提示
被除数不变 除法转化成乘法 除数转化成它的倒数
跟踪训练 计算下面各数
复习旧知
分数四则混合运算顺序先乘除、后 加减。有括号先算括 号里的。
分数除法(一)ppt课件

THANKS
感谢观看
整数除以分数的运算规则
总结词
整数除以分数等于整数乘以分数的倒 数。
详细描述
当一个整数除以一个分数时,可以将 除法转换为乘法,即将整数与分数的 倒数相乘,例如,$3 div frac{2}{3} = 3 times frac{3}{2} = 4.5$。
分数除以分数的运算规则
总结词
分数除以分数等于两分数相乘。
d/c”。
负数性质
当一个分数除以一个负数时,等于 这个分数乘以负一的倒数。即 “a/b ÷ (-c/d) = a/b × (-d/c)” 。
运算性质
分数除法具有结合律和交换律,即 “(a/b) ÷ (c/d) = (a/b) × (d/c)” 和“(a/b) ÷ (c/d) = (b/a) ÷ (d/c)”。
分数除法(一)ppt课件
CONTENTS
目录
• 分数除法的定义与性质 • 分数除法的运算规则 • 分数除法的实际应用 • 分数除法的注意事项 • 分数除法的练习题与解析
CHAPTER
01
分数除法的定义与性质
分数除法的定义
分数除法的定义
分数除法是数学中的一种基本运算, 其定义为将一个分数除以另一个分数 ,即用一个分数去除以另一个分数的 每一个分母与分子相除。
分数除法在科学计算中的应用
化学计算
在化学计算中,我们经常需要计算化学反应中各物质的质量分数或浓度,这时可以使用 分数除法。例如,计算溶液中溶质的质量分数时,可以将溶质的质量除以溶液的质量得
到质量分数。
生物计算
在生物学中,我们经常需要计算生物种群的数量或比例,这时可以使用分数除法。例如 ,计算两种生物的数量比例时,可以将一种生物的数量除以另一种生物的数量得到比例
人教版六年级数学分数除法《混合运算》省公开课获奖课件说课比赛一等奖课件
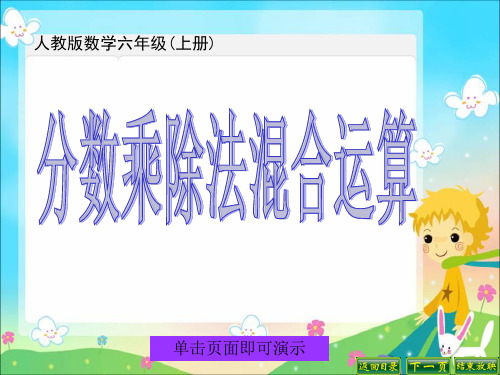
45
3 10
45
10 3
150(人)
答:六年级共有学生150人。
课堂小结:
经过这节课旳学习,你有什么收获?
人教版数学六年级(上册) 单击页面即可演示
复习
计算下列各题。 256÷8×12 =384
900+(15×6)=990
25×8÷5 =40
1050-5×10 =1000
整数混合运算旳顺序是什么?
整数混合运算旳顺序是:
从左向右,先算乘除法,后算加减法, 有括号旳先算括号里面旳。
探究新知
3
每次吃半片,
24÷3=8(天)
答:能够吃8天。
2 3
也能够用综合算式表达以上 过程,自己试着计算一下。
综合算式1: 12 (1 3) 2
12 3 2
12 2 3
8(天)
答:能够吃8天。
综合算式2:
12
1 2
3
12 2 3
24 3 8(天)
答:能够吃8天。
巩固练习
王叔叔家阁楼上旳窗玻璃是梯形旳,上底、 下底和高分别是 3 米、4 米、3 米 。这块玻璃旳
每天吃3次。
这盒药共12片, 能够吃几天?
我先算出每天 吃多少片。
措施一:
先算出每天吃多少片:
1 2
3
3(片) 2
再计算能够吃几天:
12
3 2
12
2 3
8(天)
答:能够吃8天。
也能够先算出这盒 药能够吃几次。
措施二: 先算这盒药能够吃几次
12 1 =12 2 =24(次)
2
1
再计算能够吃旳天数
554
面积是多少?
(3 4 ) 3 2 55 4
最新人教版小学六年级数学上册 第3单元 分数除法《练习八》优质课件

答:大齿轮每分钟转80周。
(4)大齿轮每分钟转80周,比小齿轮每分钟转的 周数少 4 。小齿轮每分钟转多少周? 5
解:设小齿轮每分钟转x周。
(1-
4 5
)x x
= =
80 80÷
1 5
x = 400
答:小齿轮每分钟转400周。
11.*按下面的步骤计算,再把最后的得数与开始的 数比较,你能发现什么?你知道为什么吗?
能运完?
2 4= 2 1 = 1 7 7 4 14
(1 2) 1 7 14
5 14 7
=10(车)
答:平均每车运走这批大米 的 1 ,剩下的大米还要
14
10车才能运完。
10.有一组互相咬合的齿轮。
(1)大齿轮有140个齿,小齿轮的齿数是大齿轮的 小齿轮有多少个齿?
1 5
。14Biblioteka ×1 5=28(个)
3 1 =15 5
18 12 = 39 13 2
26 13 15 = 220 25 22 3
16 (1+ 13)=12
35 (1 2)=49
7
21 ( 1 3)= 3 40 10 5 4
6. 小亮的爸爸每月工资是 5500 元,妈妈每月工资
是4500
元。他们家每月开支大约占两人工资的
3 5
新人教版小学六年级数学上册
第3单元 分数除法
练习八
练习
1.我国幅员辽阔,东西相距约5200km,东西距
离是南北的 52 。南北相距约多少千米? 55
解:设南北相距约x千米。
52 55
x x
= =
5200 5200÷
52 55
x = 5500
答:南北相距约5500千米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
果园的总面积有多少公顷
____________________________?
果园总面积 X —1— = 桃园面积 4
解:设果园的总面积有X公顷。
3 —— X
8
X X
X
= —1— 4
=
—41—
÷
3
——
8
= —41— X
8 3
= —32—
答:果园的总面积有 2 公顷。 3
(2)青湖小学修建一条塑胶跑道,____实__际__造__价_2_7_万__元__________,
花果林场里(有1桃)园桃—园38—面积公顷占,果园总面积的 1
4 果园的总面积有多少公顷?
果园总面积 X —1— = 桃园面积 4
(2)青湖小学修建实一际条造塑价胶是跑原道计,划的实际造9 价,27万元, 10
原计划造价多少万元? 原计划 X —190— = 实际造价
(1)__花_果__林_场__里_有__桃_园__—_38—___公_顷___ ,桃园面积占果园总面积的—41 ,
实际造价是原计划的 —190— , _____原__计__划__造_价__多__少__万__元__________?
原计划 X —190— = 实际造价 解:设原计划造价X 万元。
—9— X = 27
10
9
X
= 27 ÷
——
10
X = 27 X 10 9
X = 30
答:原计划造价30万元。
(3) 林地面积占国土总面积的—1—,是耕地面积的—2—5 ,
(2)乙农场大豆的种植面积是36公顷,大豆和玉米种植面 积的比是4:5。求玉米的种植面积。
探索与实践:
下面每个方格的边长表示1厘米。 (1)画一个长方形,面积是24平方厘米,长与宽的比是3:2。 (2)画一个长方形,周长是16厘米,长与宽的比是5:3。
小结: 无论是含有分数还是含有比的实际问题,我
(2)能够运用分数除法的知识去解决相关的实际 问题,提高自己解决问题的能力。
(3)通过数学游戏,体验成功的快乐,感受学数 学的乐趣。
小朋友,祝贺你
解方程:
—1— X = —3—
2
4
—7— X = —1—4 —
10
25
—3— + X = ——2 —
8
5
判断单位“1”的量,并找出数量关系。
(1)桃园面积占果园总面积的—1— 。 4
复习:
1、分数除法的计算方法怎么样? 甲数除以乙数(零除外),等于甲数乘乙数的倒数。
2、解决分数实际问题时,一般分几步进行?
①找单位“1”的量; ②看看单位“1”是已知还是未知,并写出数量关系式; ③已知单位“1”用乘法计算,求单位“1”用除法或方程解决; ④列式解答。
学习目标:
(1)通过练习,使自己熟练掌握分数除法的计算 方法,能快速并正确地进行分数除法的计算。
果园总面积 X —41— = 桃园面积
(2)实际造价是原计划的 —19—0 。
原计划 X —190— = 实际造价
(3)林地面积占国土总面积的—1—,占耕地面积的—25—。
4
13
总面积 X —41 = 林地面积
耕地面积 X —25— = 林地面积 13
补充条件和问题,使它们成为用除法或方程解决的题目。
们都可以把它们转化成分数实际问题,都可以按 照解决分数实际问题的一般方法去进行解答。
达标练习
这节课你有收获吗?
我国的国土面积大约是960万平方千米 Nhomakorabea,其中13
总面积 X —1 = 林地面积
耕地面积
林地面积大约是多4少万平方千米?林地面积大约
X
—25— 13
= 林地面积
耕地面积大约是多少平方千米?
(1)甲农场在一块36公顷的土地上种植大豆和玉米,大豆和 玉米种植面积的比是4:5。分别求大豆和玉米的种植面积。
