高等数学 第三节 三重积分
合集下载
高等数学《三重积分》课件

3
注: 1.可积性: f 连续 可积
2.物理意义
如果f(x,y,z)表示某物体在点(x,y,z)处的体密度,Ω 是该物体所占的空间闭区域,f(x,y,z)在Ω上连续, 则
物体的质量 M f ( x, y, z)dv 3.几何意义
的体积 V dxdydz
4.性质 同二重积分 4
8.3.2、直角坐标系下的三重积分的计算法
f (z, x,
y)]dV
若为球面x 2 y 2 z 2 R2所围,则
x 2dV
y 2dV
z2dV
1 3
[ x 2
y2
z 2 ]dV
13
例 3 利用对称性简化计算
z ln( x2 y2 z2 1)
x2 y2 z2 1 dxdydz 其中积分区域 {(x, y, z) | x2 y2 z2 1}.
其中A(z)是Dz的面积
习题8.3.1
20
o
y
或D(z),即
x
{( x, y, z)( x, y) Dz ,c1 z c2}
f ( x, y, z)dv c2 dz f ( x, y, z)dxdy (3)
c1 Dz
15
f (x, y, z)dv c2 dz
z
f ( x, y, z)dxdy
c1
Dz
上式的适用范围:
其中在每vi表个示v第i上i个任小取闭一区点域(,i ,也i表, 示i)它,的作体乘积积。f ( i ,
i,
i)
vi
(i=1,2,…
n
,n)
,
并作和 f (i ,i , i )vi。
如果当各i 1小闭区域直径的最大值 趋于零时
这个和的极限总存在, 则称此极限为函数
简介三重积分资料讲解

2020/7/30
三、计算xzdxdyd,z其中 是曲面z 0, z y, y 1, 以及抛物柱面y x2所围成的闭区域.
四、计算x2
1
y2
dv,其中是由六个顶点
A(1,0,0), B(1,1,0), C(1.1.2),D(2,0,0),
E(2,2,0),F(2,2,4)组成的三棱锥台.
0 1zd 0 1z z(1yz)dy
o
1
x
01z12(1z)2dz214.
y
1
2020/7/30
例5 计算三重积分 z2dxdyd,z
其中
:
x2 y2 z2 a2 b2 c2 1.
z
Dz
o
y
解
czc
x
:
x2 y2
z2
Dz :a2 b2 1c2
z2dxdydz
c z2 d z
c
dxd y
Dz
1x2dxdz
x2z21
x1
1y
计算较繁! 采用“三次积分”较好.
2020/7/30
解
1x2z2y1
z
: 1x2z 1x2
1x1
1
o 1y
1
I
1x2dx1x2
1
dz
ydy x1
1
1x2 1x2z2
1
1x2dx1x2
x2z 1x2
1x2(x2zz33)|01x2
思考: dx 若被积函数为
则 三 重 积 分 f ( x , y , z )dxdydz 化 为 三 次 积 分 是
_______________________.
2、 若
是 由 曲 面 cz
xy (c
三、计算xzdxdyd,z其中 是曲面z 0, z y, y 1, 以及抛物柱面y x2所围成的闭区域.
四、计算x2
1
y2
dv,其中是由六个顶点
A(1,0,0), B(1,1,0), C(1.1.2),D(2,0,0),
E(2,2,0),F(2,2,4)组成的三棱锥台.
0 1zd 0 1z z(1yz)dy
o
1
x
01z12(1z)2dz214.
y
1
2020/7/30
例5 计算三重积分 z2dxdyd,z
其中
:
x2 y2 z2 a2 b2 c2 1.
z
Dz
o
y
解
czc
x
:
x2 y2
z2
Dz :a2 b2 1c2
z2dxdydz
c z2 d z
c
dxd y
Dz
1x2dxdz
x2z21
x1
1y
计算较繁! 采用“三次积分”较好.
2020/7/30
解
1x2z2y1
z
: 1x2z 1x2
1x1
1
o 1y
1
I
1x2dx1x2
1
dz
ydy x1
1
1x2 1x2z2
1
1x2dx1x2
x2z 1x2
1x2(x2zz33)|01x2
思考: dx 若被积函数为
则 三 重 积 分 f ( x , y , z )dxdydz 化 为 三 次 积 分 是
_______________________.
2、 若
是 由 曲 面 cz
xy (c
高数 三重积分

均为非负函数
根据重积分性质仍可用前面介绍的方法计算.
机动
目录
上页
下页
返回
结束
小结: 三重积分的计算方法 方法1. 投影法【 “先一后二” ;“丝丝吃法”】
d xd y
D
z2 ( x, y )
z1 ( x , y )
f ( x , y , z )d z
方法2. 截面法【“先二后一” ;“片片吃法”】
z z 2 ( x, y )
z
z z1 ( x, y )
f ( x, y, z ) d v z ( x, y ) f ( x , y , z ) d z d xd y D z ( x, y )
2 1
x
D
y
d xd y
微元线密度≈
记作
D d xd y z ( x, y )
d z
a
b
DZ
f ( x, y, z )d xd y
两种方法各有特点, 具体计算时应根据 被积函数 及积分域(重积分两要素)的特点灵活选择.
机动
目录
上页
下页
返回
结束
方法1. 投影法【“先一后二” ;“丝丝吃 法 ”】 z 1) 选 择 恰 当 的 投 影 面 ,
如 闭 区 域 在 xoy 面 上的投影为闭区域 D,
I 2 f ( x , y , z )dv
3
3 ( x , y, z ) | ( x , y, z ) , x 0
x y z 例4 计算 z dv , : 2 2 2 1 a b c
2
2
2
2
例5
2 2 dxdydz , : z x y ,z 1
根据重积分性质仍可用前面介绍的方法计算.
机动
目录
上页
下页
返回
结束
小结: 三重积分的计算方法 方法1. 投影法【 “先一后二” ;“丝丝吃法”】
d xd y
D
z2 ( x, y )
z1 ( x , y )
f ( x , y , z )d z
方法2. 截面法【“先二后一” ;“片片吃法”】
z z 2 ( x, y )
z
z z1 ( x, y )
f ( x, y, z ) d v z ( x, y ) f ( x , y , z ) d z d xd y D z ( x, y )
2 1
x
D
y
d xd y
微元线密度≈
记作
D d xd y z ( x, y )
d z
a
b
DZ
f ( x, y, z )d xd y
两种方法各有特点, 具体计算时应根据 被积函数 及积分域(重积分两要素)的特点灵活选择.
机动
目录
上页
下页
返回
结束
方法1. 投影法【“先一后二” ;“丝丝吃 法 ”】 z 1) 选 择 恰 当 的 投 影 面 ,
如 闭 区 域 在 xoy 面 上的投影为闭区域 D,
I 2 f ( x , y , z )dv
3
3 ( x , y, z ) | ( x , y, z ) , x 0
x y z 例4 计算 z dv , : 2 2 2 1 a b c
2
2
2
2
例5
2 2 dxdydz , : z x y ,z 1
03第九章第3节三重积分 共40页PPT文档

1
Dzdxdy2(1z)(1z)
o
1
x
y
1
原 式 1z1(1z)2d z1.
02
24
11
例2 计算三重积分z2dxdy,d其中 z是由
椭球面ax22by22cz22 1所成的空间闭区域.
解 : {(x,y,z)|czc, ax22by221cz22}
一、 三重积分的概念
引例:设在空间有限闭区域 内分布着某种不均匀
的物质,密度函数为 f(x,y,z)C,
求分布在 内的物质的质量 M .
采用 “分割,近似,求和,取极限”
vk
n
可得 Mlim 0
f(k,k,k)vk
k 1
(k,k,k)
1
定义: 设f(x ,y,z),(x ,y,z) ,若对 作任意分割,
z
Dz
o
y
原式 cz2dz dxdy, c
x
Dz
12
z
Dz
D z{x (,y)|a x2 2b y2 21c z2 2}x
o
y
D zdxd ya2(1c z2 2) b2(1c z2 2)
ab(1cz22),
原式
ccab(1cz22)z2dz
c1 Dz
当f(x, y,z)与x, y无关时此法较. 简单
10
例 1 计 算 三 重 积 分 zdx, d其 中 y d为 三 z个
坐 标 面 及 平 面 xyz1所 围 成 的 闭 区 域 .
1
解(一)zdxdydz 0 zdzdxdy,
z
1
Dz
D z {x ,( y ) |x y 1 z }
《高等数学教学课件》 第三节 三重积分的计算法精品文档17页
分割的 .令模0, 若和式
,则f称 (x,y,z)在 上 可 积,
i1
称 极 限 f(x,值 y,z)在 为 上 的 三重积分 , 记 为 :f(x,y,z)dv,
n
即 f(x ,y,z)d v l i0 m i 1f(i,
i,
i) vi,其
中f(x , y,
z)称
为
被
积
函 ,
称f (x, y,z)dv为被积表达,式 x, y, z称为积分变量,称dv为体积微元,
(2) .由 zx,x yy1和 z0所 围 成 解(2).
xy
f(x ,y,z)dx dy d d x 0zd f(x y ,y,z)d z
D xy
1 1x xy
0dx 0 d0 yf(x,y,z)d.z
二、柱面坐标、球面坐标坐标系下的三重积分计算
1、柱面坐标系
x r cos , r [0, )
yr zr
yz rcos
zz
0
si n 0 r J r.
01
例 1、计算 zdx,其 dy 是 中 dz 由 x2 曲 y2z面 24和 x2y23z所 围 . 成
解
:
0 2
D :
0 r 3
1 3
r2
z
4 r2
zdxdyrddzrd4r2zdz 2d
3
4r2
rdr zdz
及 z1 ,z2 所 围 成 . 的 圆 台 体
解
: 1z2, "先二后一 "计算方法: (x,y)D (z):x2y2z2,
2
2
zdxdydz dz zdxd y zdz dxdy
1
1
D(z)
高数讲义第三节三重积分(一)

z 0 所围空间立体.
解 如图, Dxy : 1 x 1
x2 y 1 1
y
y x2
1 Dxy
0
1x
: 1 x 1, x2 y 1,
0 z x2 y2.
1
1
x2 y2
I
dx 1
x2
dy0
f ( x, y, z)dz.
例 2 计算三重积分 xdxdydz,其中 为三个
(5)若 是前后结构 即若用平行于 x 轴的直线穿过 ,与其边界曲面 的交点至多有两个,亦可将 投影到 yoz 面上。
f ( x, y, z)dv
而后者又可进一步化为三次积分。
对于 为左右结构情形同理。
例1 化 I f ( x, y, z)dxdydz 为三次积分,
其中, 为由曲面z x2 y2, y x2, y 1,
(3)进一步,若 是 X 型区域
z
f ( x, y, z)dv
(3) 若 是 X 型区域
o
a
Dxy {( x, y) |a x b, b y1( x) y y2( x)} x
z z2( x, y)
z2 S2
z1 S1
z z1( x, y)
D
(x, y) y y1( x)
y
y y2( x)
n
lim
0
i 1f(i,i源自,i)vi
存在,且与 的分法及点
(i ,i , i ) 的取法无关, 则称此极限为 f ( x , y, z )
在闭区域 上的三重积分,记为 f ( x, y, z)dv
n
即
f ( x, y, z)dv
lim
0
i 1
f (i ,i , i )vi .
三重积分ppt课件

dv称为体积元素, 在直角坐标系下常写作 dxdydz.
性质: 三重积分的性质与二重积分相似. 例如
2
目录 上页 下页 返回 结束 3
目录 上页 下页 返回 结束 4
二、三重积分的计算
1. 利用直角坐标计算三重积分
先假设连续函数 f (x, y, z) 0, 并将它看作某物体
的密度函数 , 通过计算该物体的质量引出下列各计算 方法:
z1( x, y)
z z1(x, y)
该物体的质量为
O
y
f (x, y, z)d v
xD
dxd y
D
z2 (x,y) f (x, y, z)dz dxdy
z1( x, y)
记作
dxd y z2 (x,y) f (x, y, z)dz
D
z1( x, y)
aπ
0 zdz 0 2 d
2cos 2 d
0
Oy 2 x 2cos
4a2 3
π 2 cos3 d
0
8a2 9
dv d ddz
10
例4. 计算三重积分
其中 由抛物面
x2 y2 4z 与平面 z h (h 0)所围成 .
微元线密度≈
f (x, y, z) dxdy
6
方法2. 截面法 (“先二后一”)
以Dz 为底, d z 为高的柱形薄片质量为
该物体的质量为
ab Dz f (x, y, z) d x d y dz
记作 b
a dzDz f (x, y, z)dxdy
z
b
z Dz
a
O
高等数学课件--D103三重积分精品

D
z2 (x,y) f (x, y, z)dz dxdy
z1( x, y)
记作
dxd y z2 (x,y) f (x, y, z)dz
D
z1( x, y)
微元线密度≈
f (x, y, z) dxdy
2019/9/1
同济版高等数学课件
目录 上页 下页 返回 结束
方法2. 截面法 (“先二后一”)
0
0
0
Oy 2 x 2cos
2019/9/1
4a2 3
π 2 cos3 d
0
8a2 9
同济版高等数学课件
dv d ddz
目录 上页 下页 返回 结束
例4. 计算三重积分
其中 由抛物面
x2 y2 4z 与平面 z h (h 0)所围成 .
z
h
解: 在柱面坐标系下
z1 ( x, (x,
y) y)
z D
z2 ( x,
y)
细长柱体微元的质量为
z z2 (x, y)
z
z2 (x,y) f (x, y, z)dz dxdy
z1( x, y)
z z1(x, y)
该物体的质量为
O
y
f (x, y, z)d v
xD
dxd y
y
其中
F(, , z) f ( cos , sin , z )
x d
d
d d d
适用范围:
1) 积分域表面用柱面坐标表示时方程简单 ;
2) 被积函数用柱面坐标表示时变量互相分离.
2019/9/1
同济版高等数学课件
同济大学 高数 三重积分ppt课件

对应雅可比行列式为 J (x, y, z) (u, v, w)
直角坐标与柱面坐标的关系:
x cos y sin zz
J (x, y, z)
(,, z)
x y
x y
xz cos sin 0
yz sin cos 0
z z zz
0
01
dv J dddz dddz
x2 y2 2
z
h
解: 在柱面坐标系下
原式 =
2π 2
d
0
0
h
1
2
d
h
2 d z
xO y
4 dv d ddz
2
2π
0
h
1
2
(h
2
4
)
d
22
目录 上页 下页 返回 结束
3. 利用球坐标计算三重积分
设 M (x, y, z) R3, 其柱坐标为(, , z), 令 OM r,
zOM ,则(r,, ) 就称为点M 的球坐标.
16
目录 上页 下页 返回 结束
f (x, y, z)dxdydz
d d dz
d
d 2 ( )
z2 (, ) F(, , z)dz
1 ( )
z1 ( , )
其中 F(, , z) f ( cos , sin , z )
(,, z) , 1( ) 2( ), z1(, ) z z2(, )
就称为点M 的柱坐标. 直角坐标与柱面坐标的关系:
x cos y sin
zz
坐标面分别为
00z2π
z z
M (x, y, z)
常数 常数
z 常数
圆柱面 半平面 平面
高等数学A10-3三重积分修订

o
y
r 3
o
A
10-3 三重积分
例8 计算三重积分 ( x2 y2 ) dv , 其中 是由曲
面 z x2 y2 与平面 z H (H 0) 所围成。
z
解: 将 向 xoy 面投影, 得
D : x2 y2 H2
HH
或 D:
0 2 ,
0 r H .
10-3 三重积分
1. 利用直角坐标计算三重积分
用平行于坐标面的平面族:x 常数,y 常数,z 常数 去分割积分区域 , 除边界外,每个小块都是一个长方体 于是得到体积微元
dv dxdydz
从而在直角坐标系下三重积分表示为:
f (x, y, z)dv f (x, y, z)dxdydz
任意划分:将 任意分成 n 个小闭区域v1, v2 vn , 其中vi表示第 i 个小闭区域,也表示它的体积.
取点作积: (i ,i , i ) vi , f (i ,i , i ) vi (i 1, 2, , n)
n
取和: f (i ,i , i ) vi . i 1
的数 r, , 来确定,其中 r 为原点 O 与点 M 间的距离,
10-3 三重积分
例 4 计算三重积分 z2dxdydz,其中 是由
椭球面 x2 a2
y2 b2
z2 c2
1所成的空间闭区域.
解: 如图所示
z
Dz
o
y
x
10-3 三重积分
例 5 计算三重积分 zdxdydz,其中 为三个
坐标面及平面 x y z 1所围成的闭区域.
三重积分 ppt课件

点不多于两个.
f (x, y, z)dv
dydz x2( y,z) f ( x, y, z)dx
Dyz
x1 ( y,z )
PPT课件
(3)Ω:平行于 y 轴且穿过区域的直线与区域边界的交
点不多于两个.
f (x, y, z)dv
dxdz y2( x,z) f ( x, y, z)dy
z z1( x, y) (x, y)
z z1( x, y)
(x, y)
10
步骤: z z2(x, y)
1、求Ω在xoy面的投影区域 ;
z z1( x, y)
2、过( x, y) Dxy做平行与 z轴的 射线 ,确定 z1( x, y) z z2( x, y) 3、
PPT课件
解 关于yoz面对称, e y2 sin x3关于x为奇函数,
PPT课件
e y2 sin x3dv 0
关于xoz面对称, yz2关于x为奇函数,
yz2dv 0
(e y2 sin x3 yz2 3)dv 3dv
3 4 三重积分的计算
(一)直角坐标
用平行坐标平面的平面
来划分区域Ω ,
v xyz dv dxdydz
f ( x, y)dxdydz
9
1、投影法
(1)Ω:平行于z轴且穿过区域的直线与区域边界的交
点不多于两个.
z z2(x, y)
z z2(x, y)
PPT课件
18
PPT课件
例4 解
19
例5
解
z
PPT课件
o
y
x
20
PPT课件
f (x, y, z)dv
dydz x2( y,z) f ( x, y, z)dx
Dyz
x1 ( y,z )
PPT课件
(3)Ω:平行于 y 轴且穿过区域的直线与区域边界的交
点不多于两个.
f (x, y, z)dv
dxdz y2( x,z) f ( x, y, z)dy
z z1( x, y) (x, y)
z z1( x, y)
(x, y)
10
步骤: z z2(x, y)
1、求Ω在xoy面的投影区域 ;
z z1( x, y)
2、过( x, y) Dxy做平行与 z轴的 射线 ,确定 z1( x, y) z z2( x, y) 3、
PPT课件
解 关于yoz面对称, e y2 sin x3关于x为奇函数,
PPT课件
e y2 sin x3dv 0
关于xoz面对称, yz2关于x为奇函数,
yz2dv 0
(e y2 sin x3 yz2 3)dv 3dv
3 4 三重积分的计算
(一)直角坐标
用平行坐标平面的平面
来划分区域Ω ,
v xyz dv dxdydz
f ( x, y)dxdydz
9
1、投影法
(1)Ω:平行于z轴且穿过区域的直线与区域边界的交
点不多于两个.
z z2(x, y)
z z2(x, y)
PPT课件
18
PPT课件
例4 解
19
例5
解
z
PPT课件
o
y
x
20
PPT课件
三重积分-高等数学PPT

dv dddz,
z
d
d
dz
o
f ( x, y, z)dxdydz
x
d
y
f ( cos , sin , z)dddz.
17
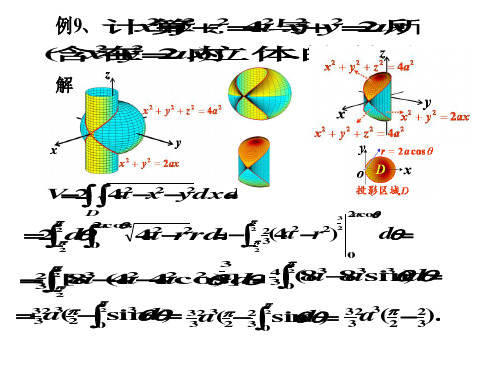
例1. 计算三重积分 z x 2 y 2 d x d yd z z
其中为由柱面 y 2 x-x2 及平面 z 0 ,
a
z a (a 0) , y 0 所围成半圆柱体.
x 2 y 2 4 z 与平面 z h (h 0) 所围成 .
h
解: 在柱面坐标系下
d xd yd z 1 x2 y2
2 2
d
0
h 0
1
2
d
h
2
d
z
o
x
y
4
2
2
h 0
1
2
(h
2
4
)d
4
[(1
4h) ln(1
4 h)
4 h]
d v d d1d9 z
例3 计算I zdxdydz,其中是球面
6
例1. 计算三重积分 xd xd yd z
z
1
其中为三个坐标面及平面 x 2 y z 1
所围成的闭区域 .
解: xdxdydz
1 2
y
x1
1
1 2
(1
x
)
1 x2 y
xdx dy dz
0
0
0
1
1 2
(1
x
)
xdx (1
x
2
y)d
y
1
1
(x
2x2
x3)d
x
1
0
0
40
z
d
d
dz
o
f ( x, y, z)dxdydz
x
d
y
f ( cos , sin , z)dddz.
17
例1. 计算三重积分 z x 2 y 2 d x d yd z z
其中为由柱面 y 2 x-x2 及平面 z 0 ,
a
z a (a 0) , y 0 所围成半圆柱体.
x 2 y 2 4 z 与平面 z h (h 0) 所围成 .
h
解: 在柱面坐标系下
d xd yd z 1 x2 y2
2 2
d
0
h 0
1
2
d
h
2
d
z
o
x
y
4
2
2
h 0
1
2
(h
2
4
)d
4
[(1
4h) ln(1
4 h)
4 h]
d v d d1d9 z
例3 计算I zdxdydz,其中是球面
6
例1. 计算三重积分 xd xd yd z
z
1
其中为三个坐标面及平面 x 2 y z 1
所围成的闭区域 .
解: xdxdydz
1 2
y
x1
1
1 2
(1
x
)
1 x2 y
xdx dy dz
0
0
0
1
1 2
(1
x
)
xdx (1
x
2
y)d
y
1
1
(x
2x2
x3)d
x
1
0
0
40
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解1 0 y 1 , y x y , 0 z 1 y
z yz1
x sin2 ydv 1sin2 ydy
y
xdx
1 y
dz
0
y
0
x
1y
0
解2 由于被积函数关于 x 是奇函数,积分域关于
yOz 平面对称,所以积分等于零。
第十章 第三节
20
奇偶对称性化简三重积分
1 积分区域关于某坐标面具有对称性; 2 被积函数在积分区域上关于相对应的坐标轴 具有奇偶性。
x 0 , y 0}
z R
R
zdxdydz 0 dz zdxdy
Dz
Dz
R
y
R x
R
z(R2
z2 )dz
(1
R2z2
1
z4)
R
R4
40
42
4 0 16
第十章 第三节
17
例6 计算 由 z 1 (x2 y2 ) , z 1 , z 4 围成。
2
解
,其中
利用对称性 轮换
奇偶
1 2
(
Dz
b
a dz f ( x , y , z)dxdy Dz
第十章 第三节
15
截面法的一般步骤:
(1) 把积分区域 向某轴 (例如 z 轴) 投影,得 投影区间 [a , b];
(2) 对 z [a , b] 用过 z 轴且平行于 xOy 面的平面
去截 ,得截面 D z ;
z b
(3) 计算二重积分 f ( x , y , z)dxdy , z
把 x 看成常数。积分区域 就为圆盘 y2 z2 x2
(1
x4
)dxdydz
4
2
dx
(1 x4 )dydz
D
y2 z2 x2
4
(1
2
x4 ) x2dx
[ x3
3
x7 7
]42
( 43 23 47 27 ) 2340 20
3
7
21
第十章 第三节
19
例8 计算三重积分 x sin2 ydv ,其中 由平面 y x , y x , z 0 , y z 1 所围成。
对调后方程不变,则将被积函数中的 x 和 z 对
调,积分也不变。即
f ( x , y , z)dv f (z , y , x)dv
Ω
Ω
轮换对称性
第十章 第三节
12
例3 计算 zdxdydz ,其中 是由
z 1 x2 y2 , z 0 围成的上半球体。
z1
x
O Dxy
1
1y
第十章 第三节
规定: 0 r
z
M(r , θ , z)
M(x , y , z)
0 2
z
O
x
r
y
P(r , θ)
第十章 第三节
23
z
如图,三坐标面分别为
r 为常数 θ 为常数 z 为常数
圆柱面 半平面 平面
M(r , , z)
z
o rP(r , )
y
x
x r cos
柱面坐标与直角坐标的关系为
z2 S2 z z2 ( x, y)
z1 S1 z z1 ( x, y)
y
Dxy
(x, y)
y y2( x)
y y1( x)
7
先将 x , y 看作定值,将 f (x, y, z) 只看作 z 的
函数,则 F ( x , y) z2 ( x , y) f ( x , y , z)dz z1 ( x , y )
, r1( ) r r2( )
(2) 确定积分区域的上下界面:
z1(r , ) z z2(r , )
y1(r , ) y y2(r , )
x1(r , ) x x2(r , )
第十章 第三节
27
例9 计算下列各题
(1) z x2 y2 dxdydz ,其中 由 y 0 , z 0 , z a
的四面体。
z 1 x yz1
O Dxy
1y
x1
x y1
第十章 第三节
11
注:若将表示积分区域 Ω 的方程中的 x 和 y 对
调后方程不变,则将被积函数中的 x 和 y 对调,
积分也不变。即
f ( x , y , z)dv f ( y , x , z)dv
Ω
Ω
同理:若将表示积分区域 Ω 的方程中的 x 和 z
第十章 第三节
3
2 三重积分的定义
设 f (x, y, z)是空间有界闭区域 上的有界函数,将
闭区域 任意分成 n 个小闭区域v1,…,vn,其
中vi 表示第 i 个小闭区域,也表示它的体积, 在每
个vi 上任取一点(i ,i , i )作乘积 f (i ,i , i ) vi ,
(i 1,2,, n),并作和, 如果当各小闭区域的直径中
vi x jykzl 三重积分记为:
n
Ω
f
(x
,
y
,
z)dxdydz
lim
0 i1
f
(i
, i
,i
)vi
其中 dxdydz=dv 叫做直角坐标系中的体积元素
第十章 第三节
5
当函数 f (x , y , z) 在闭区域 Ω 上连续时,(1) 式右 端的极限必定存在,也就是函数 f (x , y , z) 在闭区 域 Ω 上的三重积分必定存在,以后我们总假设函 数 f (x , y , z) 在闭区域 Ω 上是连续的, 关于二重 积分的一些术语都可相应地用于三重积分。 三重 积分的性质和二重积分的性质类似,这里不再重复。
o
a
x
b
b
dx
y2 ( x ) dy
z2 ( x , y) f ( x , y , z)dz
a
y1 ( x )
z1 ( x , y )
先z再y后xBiblioteka 第十章 第三节yD (x, y) xy y y2 ( x) y y1( x)
8
(1) 这时平行于 z 轴且穿过闭区域 Ω 内部的直 线与闭区域 Ω 的边界曲面 S 相交不多于两点。 (2) 如果平行于 x 轴或 y 轴且穿过闭区域 Ω 内 部的直线与 Ω 的边界曲面 S 相交不多于两点, 也可以把闭区域 Ω 投影到 yOz 面上或 xOz 面上, 这样便把三重积分化为按其他顺序的三次积分。 (3) 如果平行于坐标轴且穿过闭区域 Ω 内部的 直线与边界曲线 S 的交点多于两个,也可像处 理二重积分那样,把 Ω 分成若干部分,使 Ω 上 的三重积分化为各部分闭区域上的三重积分和。
2 被积函数用柱面坐标表示时变量互相分离。即
f g( x2 y2 ) h(z) ; f g( x2 y2 , z)
3
被积函数形如
f (x2
y2 )z
,
f
y x
z
,
f
x y
z
。
第十章 第三节
26
利用柱面坐标的解题程序:
(1) 将积分区域向坐标面 xOy (xOz 或 yOz) 作投影, 并用极坐标表示投影区域:
小块,只要小块所占的闭区域 △Vi 的直径很小, 这小块就可以看作是均匀体, 在 △Vi 上任取一点
(i , i , i )则: (i , i , i ) Vi (i 1 , , n) 可看作第 i 个小块的质量之近似值,通过求和,取极限,便 得到质量
n
m lim 0
i 1
(i
, i
, i )Vi
1 问题的引入 设有一物体,在空间直角坐标系中,占有第一卦限的 一个闭区域 Ω ,点 (x , y , z) 处的密度为 ρ(x , y , z) , ρ(x , y , z)>0 且在 Ω 上连续,现在要计算该物体的质 量。解决方法:
“分割 , 近似 , 求和 , 取极限”
第十章 第三节
2
由于 ρ(x , y , z) 在 Ω 上连续, 把 Ω 任意分为 n 个
第十章 第三节
6
二、三重积分的计算
1 利用直角坐标计算三重积分
(1) 投影法(先一后二)
z
如图:闭区域 Ω 在 xOy
面上的投影为闭区域 Dxy
S1 : z z1( x, y)
S2 : z z2( x, y)
o
a
过点 ( x, y) Dxy 作直线 b
x
从 z1 穿入,从 z2 穿出
第十章 第三节
的最大值 趋近于零时,这和式的极限存在,则称
此极限为函数 f ( x, y, z)在闭区域 上的三重积分,
记为 f ( x, y, z)dv,
n
f(x ,
y,
z)dv
lim 0
i 1
f (i
, i
, i )vi
(1)
其中 dv 叫做体积元素
第十章 第三节
4
在直角坐标系中,如果用平行于坐标面的平面 来划分 Ω ,则:
第三节 三重积分
教学内容
1 三重积分的定义与性质; 2 三重积分在直角坐标系下的计算; 3 三重积分在柱面坐标系下的计算; *4 三重积分在球面坐标系下的计算;
考研要求
1 理解三重积分的概念,了解其性质; 2 会计算三重积分(直角坐标 , 柱面坐标 , 球面坐标)
第十章 第三节
1
一、三重积分的概念
第十章 第三节
9
例1 将三重积分 f (x , y , z)dv 化为直角坐标下
Ω
的三次积分,积分区域由曲面 z x2 2 y2 , z 2 x2
所围成。
第十章 第三节
