21物质波及统计解释
§16.2 物质波的波函数,玻恩的统计解释
§16.2 物质波的波函数，玻恩的统计解释（一）物质波的波函数ψ（r ，t ）在第三篇§10.1（四）已谈过，一个频率为ν、波长为λ，沿x 轴传播的平面简谐机械波，其中各个质点的振动位移函数y （x ，t ）可表示如下：()λ-νπ=⎥⎦⎤⎢⎣⎡x t 2cos A )t ,x (y 机械波的位移函数单频率平面简谐 （16.2.1） 此式的y 表示：t 时刻、在x 位置的质点，离开平衡位置的位移．A 为质点的振幅．我们曾经用此式计算机械波的能量和干涉现象等． 在第三篇§11.1（一）描述电磁波时，将上式的y 改为电场强度E y 和磁场强度H z ：⎥⎦⎤⎢⎣⎡电磁波的表式单频率平面 ()()λ-νπ=λ-νπ=x t 2cos H H x t 2cos E E 0z z 0y y利用复数的欧拉公式，可将上述余弦函数与指数函数联系起来❶：〔欧拉公式：〕 （16.2.4）根据上式可把上述机械波和电磁波表式写成复数形式，例如：〔单频率平面机械波的复数表式〕)/x t (2i Ae )t ,x (y λ-νπ-=（16.2.5）表式（16.2.1）就是（16.2.5）复数表式的实数部分．可以设想，物质波的波函数ψ（x ，t ）也可仿照上式写出：⎥⎦⎤⎢⎣⎡其物质波的波函数轴运动的自由粒子沿,x （16.2.6）这里所说自由粒子，指的是没受外力作用的微观粒子，它的总能ε和动量p 都是不变量，与它缔合的物质波的频率ν和波长λ也是不变量．按波粒二象性的关系式（16.1.4）和（16.1.5），可用ε和p 代替（16.2.6）式中的ν和λ：⎥⎦⎤⎢⎣⎡其物质波的波函数轴运动的自由粒子沿,x 16.2.7）物质波的波函数要用复数表式，其原因请看（16.3.3）式后面的说明．如果自由粒子在三维空间中运动，则上式的px 应改为p ·r ，波函数应写为ψ（x,y,z,t ）或ψ（r ，t ）：⎥⎦⎤⎢⎣⎡自由粒子的波函数在三维空间中运动的 （16.2.8）❶ 同济大学数学教研室主编《高等数学》下册223—224页，1978年版.（16.2.2） （16.2.3）（16.2.12） （16.2.13）（二）物质波波函数的统计解释物质波波函数ψ（r ，t ）的物理意义如何?这在当时有过不少争论．后来，多数物理学家逐渐接受了玻恩于1926年提出的统计解释．在第三篇§11.1介绍光波时，曾经说过光波的强度与它的振幅平方成正比．现在按光子的观点，光的强度与它的光子数成正比，如（15.2.7）式所示．因此，光子数应与它的光波的振幅平方成正比．对于物质波，应与光波有相似的结论：在某一时刻，入射于空间某处的实物粒子数，应与该处的物质波波函数的模的平方成正比．也就是说，在某一时刻，在空间某一地点，粒子出现的几率，正比于该时刻、该地点的波函数的模的平方．用关系式表示如下：在t 时刻，粒子出现在（x,y,z ）处的体积元dV=dxdydz 内的几率∝|ψ(r ，t)|2dxdydz=|ψ(r ，t)|2dV ．在t 时刻，粒出现在（x,y,z ）处的几率密度∝|ψ(r ，t)|2． （16.2.9）虚数不能表示实际的物理量，含有虚数的复数也不能表示物理量．但是，如〔附录16A 〕所示，复数的模是实数，可以表示现实的物理量．如（16.2.9）式所示，用波函数的模的平方可以表示微观实物粒子出现的几率密度（即单位体积内，粒子出现的几率），其表式如下： 〔微观粒子的几率密度〕 （16.2.10）这就是1926年玻恩提出的波函数ψ的统计解释．因此，物质波也称为几率波．用几率来表示微观粒子的运动，包括量子物理的创始人普朗克、爱因斯坦、德布罗意等所迟迟未予确认．因此，延迟20多年，玻恩才于1954年获得诺贝尔奖金．（三）物质波波函数ψ的条件（1）波函数的标准条件在某一时刻t ，在空间某一定点（x,y,z ），微观粒子出现的几率应是唯一的、有限的数值，随着时间和位置的变化，上述几率应是连续变化的．这就要求波函数ψ必须是一个单值、有限和连续的函数．这称为波函数的标准条件．（2）波函数的归一化条件在时刻t ，粒子出现在（x,y,z ）处的几率为|ψ|2dV ．在整个运动空间V 内，粒子出现的几率总和应为1．其表式如下：〔波函数的归一化条件〕 （16.2.11） （四）非相对论的波函数本教材只讨论非相对论的波函数，也就是只讨论粒子速度v <<c 的情况．对此情况，粒子的总能ε与能量E 和动量p 的关系，可用经典力学的关系式来表示．对于自由粒子，由于没受外力作用，其势能E p =0，其能量E 就等于其动能E k ．⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡ε<<总能自由粒子的时,c v m 2/p mc 2/m mc E E m 2/p 2/m E E E E .m m ,0E 2222022k p k 0p+=+=+=ε===+===v v 如〔附录16B 〕所示，计算v <<c 的粒子的几率密度|ψ|2时，静能E 0=m 0c 2不起作用．因❶ 杨建邺，止戈编著《杰出物理学家的失误》137、140页，华中师范大学出版社1986年版.、 此，可用能量E 代替（16.2.7）式中的总能ε，以表示自由粒子的波函数ψ❶．⎥⎦⎤⎢⎣⎡<<时的波函数子轴运动的自由粒沿c x v（16.2.14）此式亦可推广于（16.2.8）式：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡<<波函数时的自由粒子c v （16.2.15）❶〔美〕E ·H ·威切曼著，复旦大学物理系译《量子物理学》《伯克利物理学教程》第四卷340—341页，1978年版.。
教学：物质波
二、电子的双狭缝干涉：
2.电子双狭缝干涉实验：
(本世纪初，物理学家评为最美丽的10个历史实验中的第一名)
(1)1961年，德国科学家首先成功地制造出非常细小 的狭缝，当电子通过此狭缝后，可得到很清晰的 干涉条纹。
二、电子的双狭缝干涉：
2.电子双狭缝干涉实验：
(本世纪初，物理学家评为最美丽的10个历史实验中的第一名)
ቤተ መጻሕፍቲ ባይዱ
三、波粒二象性与量子论：
※图8-9：
说明： γ射线（无法呈现在照 片中）自左端进入，与 氢原子碰撞后，出现的 电子(小螺旋)与正子 (大螺旋)及氢原子(长 线)的运动轨迹。
而是具有特定的数值 h f， 此值也称为能量量子（energy quantum) 。
三、波粒二象性与量子论：
5.量子论（quantum theory）：
探讨辐射与原子交互作用时的光量子行为，以 及在微观尺度内基本粒子与其他相关的量子化 特性，所发展出来的理论。
在微观尺度下，牛顿运动定律因无法诠释 这些量子化现象，而不再适用。
2.电子也具有波粒二象性：
因此电子行为到底是波或粒子，须依据所执行 的实验来决定。
三、波粒二象性与量子论：
光有时是波， 有时是粒子
电子有时是粒 子，有时是波
三、波粒二象性与量子论：
4.光的能量量子化（quantized）：
光的粒子性表示电磁波在微观尺度中，与原子 交互作用的能量不是与振幅有关，也不可具有 任何连续值。
1.光具有波粒二象性（wave-particle duality）：
波动性：
电磁辐射（含可见光、X光、微波、 ⋯⋯ 等）在 传播行进时，它们集体地散布或占据较大空间 ，也可产生干涉与绕射现象。
北师大-结构化学课后习题答案
北师大 结构化学 课后习题 第一章 量子理论基础习题答案1 什么是物质波和它的统计解释？参考答案:象电子等实物粒子具有波动性被称作物质波。
物质波的波动性是和微粒行为的统计性联系在一起的。
对大量粒子而言，衍射强度（即波的强度）大的地方，粒子出现的数目就多，而衍射强度小的地方，粒子出现的数目就少。
对一个粒子而言，通过晶体到达底片的位置不能准确预测。
若将相同速度的粒子，在相同的条件下重复多次相同的实验，一定会在衍射强度大的地方出现的机会多，在衍射强度小的地方出现的机会少。
因此按照波恩物质波的统计解释，对于单个粒子，ψψ=ψ*2代表粒子的几率密度，在时刻t ，空间q 点附近体积元τd 内粒子的几率应为τd 2ψ；在整个空间找到一个粒子的几率应为 12=ψ⎰τd 。
表示波函数具有归一性。
2 如何理解合格波函数的基本条件？ 参考答案合格波函数的基本条件是单值，连续和平方可积。
由于波函数2ψ代表概率密度的物理意义，所以就要求描述微观粒子运动状态的波函数首先必须是单值的，因为只有当波函数ψ在空间每一点只有一个值时，才能保证概率密度的单值性；至于连续的要求是由于粒子运动状态要符合Schrödinger 方程，该方程是二阶方程，就要求波函数具有连续性的特点；平方可积的是因为在整个空间中发现粒子的概率一定是100%，所以积分⎰τψψd *必为一个有限数。
3 如何理解态叠加原理？ 参考答案在经典理论中，一个波可由若干个波叠加组成。
这个合成的波含有原来若干波的各种成份（如各种不同的波长和频率）。
而在量子力学中，按波函数的统计解释，态叠加原理有更深刻的含义。
某一物理量Q 的对应不同本征值的本征态的叠加，使粒子部分地处于Q 1状态，部分地处于Q 2态，……。
各种态都有自己的权重（即成份）。
这就导致了在态叠加下测量结果的不确定性。
但量子力学可以计算出测量的平均值。
4 测不准原理的根源是什么？ 参考答案根源就在于微观粒子的波粒二象性。
北师大版结构化学 习题答案
第一章思考题和习题1 什么是物质波和它的统计解释？2 如何理解合格波函数的基本条件？3 如何理解态叠加原理？4 测不准原理的根源是什么？5 铝的逸出功是4.2eV ，用2000Å的光照射时，问（a ）产生的光电子动能是多少？(b)与其相联系的德布罗依波波长是多少？(c)如果电子位置不确定量与德布罗依波波长相当，其动量不确定量如何？6 波函数e -x (0≤x ≤∞)是否是合格波函数，它归一化了吗？如未归一化，求归一化常数。
7 一个量子数为n ，宽度为l 的一维势箱中的粒子，①在0~1/4 区域内的几率是多少？②n 取何值时几率最大？③当n →∞时，这个几率的极限是多少？ 8 函数x ll x l l x ππψ2sin 22sin 23)(+=是不是一维势箱中粒子的可能状态？如果是，其能量有无确定值？如果有，是多少？如果能量没有确定值，其平均值是多少？ 9 在算符∑，错误！未定义书签。
, exp, 错误！未定义书签。
中，那些是线性算符？10 下列函数, 那些是错误！未定义书签。
的本征函数? 并求出相应的本征值。
(a) e imx (b) sin x (c) x 2+ y 2 (d) (a -x )e -x11 有算符,ˆ,ˆX X dx d D== 求D X X D ˆˆˆˆ-。
参考答案1 象电子等实物粒子具有波动性被称作物质波。
物质波的波动性是和微粒行为的统计性联系在一起的。
对大量粒子而言，衍射强度（即波的强度）大的地方，粒子出现的数目就多，而衍射强度小的地方，粒子出现的数目就少。
对一个粒子而言，通过晶体到达底片的位置不能准确预测。
若将相同速度的粒子，在相同的条件下重复多次相同的实验，一定会在衍射强度大的地方出现的机会多，在衍射强度小的地方出现的机会少。
因此按照波恩物质波的统计解释，对于单个粒子，ψψ=ψ*2代表粒子的几率密度，在时刻t ，空间q 点附近体积元τd 内粒子的几率应为τd 2ψ；在整个空间找到一个粒子的几率应为 12=ψ⎰τd 。
量子力学 第二章 波函数和薛定谔方程
x px
t E J
二.量子力学中的测量过程 1.海森伯观察实验 2.测量过程 被测对象和仪器，测量过程即相互作用过程，其影响 不可控制和预测。
三.一对共轭量不可能同时具有确定的值是微观粒 子具有波动性的必然结果。
并不是测量方法或测量技术的缺陷。而是在本质上 它们就不可能同时具有确定的值
i p
p2 2
对自由粒子：
2 E p
2
∴
2 i 2 t 2
3.力场中运动粒子的波动方程 能量关系：
E p2 U (r , t ) 2
2 i 2 U (r , t ) t 2
4.三个算符
2 H 2 U 2
1。与宏观粒子运动不同。
2。电子位置不确定。
3。几率正比于强度，即 ( r , t )
2
结论：
波函数的统计解释：波函数在空间某一点的 强度（振幅绝对值的平方）和在该点找到粒 子的几率成正比。
2 数学表达： (r , t ) | (r , t ) |
归一化：
2 (r , t )d | (r , t ) | d 1
3 2 i ( pr Et )
e
(r ) p
1 (2)
3 2
e
i pr
(r , t )
( r ) dp dp dp x y z c( p, t ) p
其中：
而：
i Et c( p, t ) c( p) e
而在晶体表面反射后的晶电子状态
状态的迭加。
p
为各种值的
物质波
概念由来
1
基本概念
2
粒子观点
3
波动观点
4
补充资料
5
实验证明
物质波（德布罗意波）（matter wave）指物质在空间中某点某时刻可能出现的几率，其中概率的大小受波 动规律的支配。
比如一个电子，如果是自由电子，那么它的波函数就是行波，即是说它有可能出现在空间中任何一点，每点 几率相等。如果被束缚在氢原子里，并且处于基态，那么它出现在空间任何一点都有可能，在波尔半径处几率最 大。对于你自己也一样，你也有可能出现在月球上，和你坐在电脑前的几率相比，这是非常非常小的，以至于不 可能看到这种情况。这些都是量子力学的基本概念，非常有趣。
合并图册
量子力学认为物质没有确定的位置，在不测量时，它出现在哪里都有可能，一旦测量就得到它的其中一个本 征值即观测到的位置。对其它可观测量亦呈现出一种分布，观测时得到其中一个本征值，物质波于宏观尺度下表 现为对几率波函数的期望值，不确定性失效可忽略不计。
量子力学里，不对易的力学量，比如位置和动量是不能同时测量的，因此不能得到一个物体准确的位置和动 量，位置测量越准，动量越不准，这个叫不确定性原理。哲学认为，不可能被观测的值相当于不存在，因此，根 据量子力学，不存在同时拥有准确的动量和位置的粒子。机械波是周期性的振动在媒质内的传播，电磁波是周期 变化的电磁场的传播。物质波既不是机械波，也不是电磁波。
大学物理课件---物质波的统计解释---[福州大学...李培官]
![大学物理课件---物质波的统计解释---[福州大学...李培官]](https://img.taocdn.com/s3/m/8301a54127284b73f2425060.png)
14
欢迎指导
谢谢
今天是2020年1月6日星期一
15
10
机械波: -位移量在空间传播 y Acos(t- x )
电磁波: -电场强度在空间传播
E
E0
cos(tu- x
u
)
实物波: ---粒子在空间出现的几率的分布
以电子单缝衍射为例:
光强
亮
暗
x波动观点: I A2 A大 A小
φ
电子束
粒子观点: I N光子数N密大度 N小
统计观点: I 几率 几率大 几率小
今天是2020年1月6日星期一
大学物理课件
--物质波的统计解释
福州大学至诚学院
大学物理教研室 李培官
1
第六篇
第十二章. ---波和粒子
2
§12--2.物质波.不确定关系
§12-2--2.
物质波的统计解释
3
一.电子双缝衍射实验
机械波是机械振动在介质中的传播，电磁波是变化 的电磁场在空间的传播,那么实物粒子波是什么形式 呢?
这种看法与实验不符。我们知道，衍射现象是由波的干涉而 产生的，如果波真是由它所描写的粒子所组成，则粒子流的衍 射现象应当是由于组成波的这些粒子相互作用而形成的。但事 实证明，在粒子流衍射实验中，照象片上所显示出来的衍射图 样和入射粒子流强度无关，也就是说和单位体积中粒子的数目 无关。如果减小入射粒子流强度，同时延长实验的时间，使投 射到照象片上粒子的总数保持不变，则得到的衍射图样将完全 相同。即使把粒子流强度减小到使得粒子一个一个地被衍射， 照片上一次出现一个孤立的点，体现了电子的粒子性。只要经 过足够长的时间，所得到的衍射图样也还是一样。这说明每一 个粒子被衍射的现象和其他粒子无关，衍射图样不是由粒于之 间的相互作用而产生的。
波函数及薛定谔方程
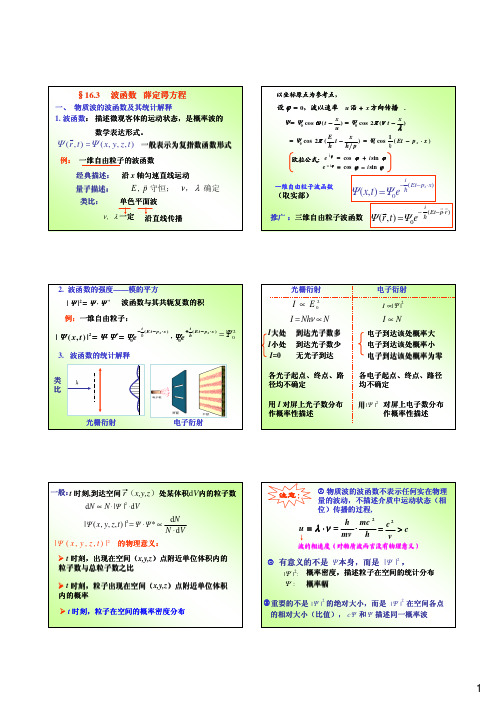
t 时刻，出现在空间（x,y,z）点附近单位体积内的 粒子数与总粒子数之比
t 时刻，粒子出现在空间（x,y,z）点附近单位体积 内的概率
t 时刻，粒子在空间的概率密度分布
注意：
物质波的波函数不表示任何实在物理 量的波动，不描述介质中运动状态（相 位）传播的过程,
NN
标准条件
Ψ是单值、有限、连续的 。
二、薛定谔方程： 是波函数 Ψ所遵从的方程 — 量子力学的基本方程 , 是量子力学的基本假设之一，其正确性由实验检验。
1. 建立 （简单→复杂， 特殊→一般）
一维自由粒子的振幅方程
Ψ (x,t)
=Ψ e−
i ℏ
(
E
t
−
px
⋅
x
)
0
=
Ψ
0e
+
i ℏ
p
x
⋅x
−i Et
2 x
2m
代入
d2ψ ( x) dx2
=
−
px ℏ2
2
ψ
(
x
)*
得
d 2ψ ( x ) dx2
+
2 mE ℏ2
ψ
(x)
=
0
即 一维自由粒子的振幅方程
p
2 x
=
2mE
一维定态薛定谔方程
粒子在力场中运动，且势能不随时间变化
E
=
Ek
+
Ep
=
p
2 x
2m
+U
px2 = 2m(E −U )
代入
d2ψ ( x) dx2
∴ 建立关于振幅函数 ψ(x)的方程 —— 振幅方程
波函数及其统计解释
在实验中可以控制电子枪的电压，使发出的电子束的 强度十分微弱，以至电子是一个一个通过。假如时间不 长，则落在屏幕上的是一个个的点，而不是扩散开的衍 射图案。就这个意义而言，电子是粒子而不是扩展开的 波。
但时间一长，则感光点在屏幕上的分布显示衍射图样， 与强度较大的电子束在较短时间内得到的图样相同。可 以认为：尽管不能确定一个电子一定到达照相底片的什 么地方，但它到达衍射图样极大值的几率必定较大，而 到达衍射图样极小值的地方的几率必定较小，甚至为零。
在量子物理中，却将这种波方程的复数表示借用过来， 并不再取它的实部，而赋予它新的物理意义。即 用它表示微观客体的波粒子二象性，它就是波函数。
在量子力学中，粒子的状态用波函数来描写，根据薛 定谔方程得出波函数的变化规律。如果已知波函数，则 可由它求出所有描述粒子状态的物理量。
在量子物理中，波函数常用ψ(x,y,z,t)表示，它的最简 单的一个表示式为
3.3 波函数及其统计解释
一、波函数 二、波函数的统计解释 三、波函数的标准条件和归一化
一、波函数
在经典力学中，我们只要知道了质点的运动 方程及其初始条件，就可以知道它的确切位置 和动量。这种方法在宏观世界取得很大的成功， 但不能适用于具有波粒二象性的微观粒子。
量子力学原理之一：微观粒子的状态可用 波函数来描述。
在经典物理中，为了计算方便，常将波方程表示成 复数，如单色平面波
y( x, t) Acos(t kx)
表示为Y ( x, t ) Aei(tkx)
显然，y（x，t）等于Y（x，t）的实部，这样计算时 用Y（x，t），算完后再取它的实部，这样做在经典物 理中是为了计算的方便，在物理学中并无新意。
物质波与德布罗意假说
物质波与德布罗意假说物质波与德布罗意假说是量子力学的重要基础理论之一。
它由法国物理学家德布罗意于1924年提出，为后来的量子力学的发展奠定了基础。
本文将介绍物质波的概念、德布罗意假说的内容以及其在量子力学中的应用。
一、物质波的概念物质波是指物质粒子具有波动性质的现象。
在经典物理学中，物质被认为是由粒子组成的，其运动遵循牛顿力学的规律。
然而，德布罗意假说的提出改变了这一观念。
根据德布罗意假说，不仅电磁波具有粒子性质，物质粒子也具有波动性质。
德布罗意假说的核心思想是，对于具有动量p的物质粒子，存在一个与其相关的波长λ，即德布罗意波长。
这个波长与物质粒子的动量之间存在着简单的关系，即λ=h/p，其中h为普朗克常数。
这意味着物质粒子的波动性质与其动量密切相关。
二、德布罗意假说的内容德布罗意假说的提出，为量子力学的发展提供了重要的理论基础。
根据德布罗意假说，物质粒子的波动性质可以通过波函数来描述。
波函数是一个数学函数，它描述了物质波的性质，包括波的振幅、相位等信息。
德布罗意假说还提出了波函数的演化方程，即薛定谔方程。
薛定谔方程描述了物质波的演化规律，可以用来计算物质波在空间中的分布和变化。
通过求解薛定谔方程，可以得到物质波的波函数，从而得到物质粒子的波动性质。
德布罗意假说还指出，物质波的波函数的平方值，即波函数的模方，可以解释为物质粒子在空间中的概率分布。
这意味着物质粒子的位置、动量等物理量不再具有确定的值，而是具有一定的概率分布。
这与经典物理学中的确定性观念有所不同，体现了量子力学的概率性质。
三、物质波的应用物质波的概念和德布罗意假说的内容在量子力学中有广泛的应用。
首先，物质波的波函数可以用来描述粒子在空间中的运动和行为。
通过求解薛定谔方程，可以得到物质波的波函数，从而得到粒子的波动性质。
其次，物质波的波函数的模方可以解释为粒子在空间中的概率分布。
这意味着我们可以通过物质波的波函数来计算粒子在不同位置、不同动量下的概率分布，从而得到粒子的统计性质。
波函数及其统计解释
动量分布概率（1）
设子设有平出 动 面pr现 量波 px在的ixip点波的y函pjr概y数j附z率k为近p如，zk的何则为概表(|粒r率示)(子r。？) 的|2eip动|r /量(x,，y, z那) |2么表粒示子粒具
任意粒子的波函数可以按此平面波做傅立叶展开
(r )
1
(2)3
2
( p)eipr / d 3 p
*
(
p)
p
(
p)d
3
p
p
*
(r )
pˆ
(r )d
3r
,
pˆ
力学量用算符表示
A
*
(r )
Aˆ
(r )d
3r
20
三、力学量用算符表示(5)
力学量 A 的平均值为
A
*
(r )
Aˆ
(r )d
3r
其 问中 题，：Aˆ坐为标力r学的量平A均的值算符r 。
*
(r )r
(r )d
该如何理解波函数的物理意义？为此，人们
提出了波函数的统计诠释来作为对波函数物
理意义的一种理解。
4
量子力学的基本假定之一
基本假定Ⅰ：波函数假定 微观粒子的状态可以被一个波函数完全 描述，从这个波函数可以得出体系的所 有性质。波函数一般满足连续性、有限 性和单值性三个条件。 说明：波函数一般是粒子坐标和时间的 复函数，波函数的模方代表粒子空间分 布的概率密度。
量子力学
波函数及其统计解释 粒子的动量分布 不确定度关系——进一步讨论
1
简短回顾
1、自由粒子的波函数 既然粒子具有波动性，那么就应该用一
个反映波动的函数来加以描述。 由平面波公式 Asin(kxt)
北师大-结构化学课后习题答案
北师大 结构化学 课后习题 第一章 量子理论基础习题答案1 什么是物质波和它的统计解释？参考答案:象电子等实物粒子具有波动性被称作物质波。
物质波的波动性是和微粒行为的统计性联系在一起的。
对大量粒子而言，衍射强度（即波的强度）大的地方，粒子出现的数目就多，而衍射强度小的地方，粒子出现的数目就少。
对一个粒子而言，通过晶体到达底片的位置不能准确预测。
若将相同速度的粒子，在相同的条件下重复多次相同的实验，一定会在衍射强度大的地方出现的机会多，在衍射强度小的地方出现的机会少。
因此按照波恩物质波的统计解释，对于单个粒子，ψψ=ψ*2代表粒子的几率密度，在时刻t ，空间q 点附近体积元τd 内粒子的几率应为τd 2ψ；在整个空间找到一个粒子的几率应为 12=ψ⎰τd 。
表示波函数具有归一性。
2 如何理解合格波函数的基本条件？ 参考答案合格波函数的基本条件是单值，连续和平方可积。
由于波函数2ψ代表概率密度的物理意义，所以就要求描述微观粒子运动状态的波函数首先必须是单值的，因为只有当波函数ψ在空间每一点只有一个值时，才能保证概率密度的单值性；至于连续的要求是由于粒子运动状态要符合Schrödinger 方程，该方程是二阶方程，就要求波函数具有连续性的特点；平方可积的是因为在整个空间中发现粒子的概率一定是100%，所以积分⎰τψψd *必为一个有限数。
3 如何理解态叠加原理？ 参考答案在经典理论中，一个波可由若干个波叠加组成。
这个合成的波含有原来若干波的各种成份（如各种不同的波长和频率）。
而在量子力学中，按波函数的统计解释，态叠加原理有更深刻的含义。
某一物理量Q 的对应不同本征值的本征态的叠加，使粒子部分地处于Q 1状态，部分地处于Q 2态，……。
各种态都有自己的权重（即成份）。
这就导致了在态叠加下测量结果的不确定性。
但量子力学可以计算出测量的平均值。
4 测不准原理的根源是什么？ 参考答案根源就在于微观粒子的波粒二象性。
波函数
练习： 3.在何处找到粒子的概率最大？
解： 1. 由归一化条件
A
1 ix
2
dx
A2 1 x2
dx
A2arctgx
A2
1
得： A 1
x
1
1 ix
2. 概率密度为：
p x2
dx
2
1
1 ix
1
1
x2
3. 令： 得：
d x2 0
dx
x0
即在 x = 0 处粒子的概率密度最大。
求解问题的步骤：
1. 写出具体问题中势函数U(r)的形式，代入一维定态 薛定谔方程的一般形式，得本问题中的薛定谔方程。
设粒子在一维无限深势阱运动
U
势函数
0 (0 < x < a)
U(x) =
x 0, x a
o
ax
代入一维定态薛定谔方程的一般形式
d2
d x2
2m 2
(
E
U )
0
得本问题中的薛定谔方程: 0<x<a
用 |Ψ |2 对屏上电子数分布 作概率性描述
一般：t 时刻,到达空间 r（x,y,z）处某体积dV内的粒子数
dN N |Ψ |2 dV
|Ψ (x, y, z,t) |2 Ψ Ψ* dN N dV
|Ψ ( x, y, z, t) |2 的物理意义：
➢ t 时刻，出现在空间（x,y,z）点附近单位体积内的 粒子数与总粒子数之比
t
)
0e
i(
Et
px
x)
（取实部）
推广 ：三维自由粒子波函数
(r,
t)
0e
i (Et
德布罗意物质波和玻恩对波函数的统计解释
德布罗意物质波和玻恩对波函数的统计解释摘要德布罗意物质波概念的提出看似充满了大胆的假设色彩，但其背后却包含了物理研究过程中重要的类比思想，同时，对波函数的解释颠覆了以往人们对经典波动理论的理解，开创了量子力学的时代。
关键词物质波；波函数；几率德布罗意在爱因斯坦的光子学说的启示下，通过对几何光学和经典力学的对比，大胆的提出了物质波的假设，促进了物理学的发展。
1 德布罗意物质波假设20世纪20年代前后，有关原子结构和量子理论的研究引起了当时很多物理学家的关注。
爱因斯坦的光量子理论通过密立根、康普顿等人的研究得到了证实，德布罗意对此发生了很大的兴趣，他认为在对光的研究过程中，同时引进了粒子概念和周期性概念，光本身必须同时考虑粒子性和波动性。
他进一步研究了几何光学和经典力学的对应性，几何光学中的费马原理和经典力学中的莫培丢变分原理类似，他大胆设想，不仅光具有粒子性和波动性两种性质，而且一般的物质也具有这两种性质。
德布罗意认为：既然粒子概念在波的领域里成功的解释了令人困惑的光电效应，那么，波动概念也应该能解释在粒子领域中令人困惑的定态问题。
1923年~1924年期间，德布罗意陆续发表了《波和粒子》、《光量子，衍射和干涉》等论文，提出了物质波的概念，他认为一个能量为E ，动量为P 的粒子与频率为，波长为的波相对应。
仿照爱因斯坦关系，粒子的能量、动量与相应的频率、波长之间的关系为：这个关系我们称之为德布罗意关系。
在此基础上，他用物质波概念分析了玻尔量子化条件的物理基础。
氢原子中电子波绕原子核的圆周轨道传播一周后应光滑的连接在一起，否则将会由于干涉相互抵消，不能形成稳定轨道。
这就要求轨道的周长应是波长的整数倍，即满足：式中r是电子绕核的轨道半径，是电子波的波长。
利用德布罗意关系，可以得出玻尔量子化条件：德布罗意的物质波假设在当时并没有引起很大的注意，原因为：首先，这个假设只是对玻尔的量子化条件提供了一个解释方案，并没有得出新的结论。
物质波
17
物质波振幅的平方与粒子在该处邻近出现的概率 成正比。 成正比。 电子出现的概率反映该处的波强。 电子出现的概率反映该处的波强。 粒子观点 波动观点 波强 电子密处，概率大。 电子密处，概率大。 电子疏处，概率小。 电子疏处，概率小。 电子密处，波强大。 电子密处，波强大。 电子疏处，波强小。 电子疏处，波强小。 振幅A 粒子密度 ∝ 振幅 2
13
h h λ= = 2me eU P
再由： 再由：
2d sin ϕ = kλ
−31
U = 54V, me = 9.11 × 10
6.63 × 10 −34
−31 −19
Kg
λ=
×1.6 × 10 × 54 180 − 50 电子衍射掠射角： 电子衍射掠射角： ϕ = = 650 2 镍单晶 d = 0.91×10 −10 m, ϕ = 650
∝
概率
机械波是机械振动在空间传播， 布罗意波是对 机械波是机械振动在空间传播，德布罗意波是对 微观粒子运动的统计。 微观粒子运动的统计。
18
二、不确定关系
经典力学中，物体初始位置、 经典力学中，物体初始位置、动量以及粒子所在 力场的性质确定后，物体以后的运动位置就可确定。 力场的性质确定后，物体以后的运动位置就可确定。 但对微观粒子，因具有的波动性， 但对微观粒子，因具有的波动性，其坐标和动量不能 同时确定。我们不能用经典的方法来描述它的粒子性。 同时确定。我们不能用经典的方法来描述它的粒子性。 1.电子单缝衍射 1.电子单缝衍射
2
= 8.73×10 (m)
7
−13
（4）当EK= 1GeV 时，k >> m0 c 2 ） E 有： hc
，
λ=
北师大_结构化学课后习题答案
北师大 结构化学 课后习题第一章 量子理论基础习题答案1 什么是物质波和它的统计解释？参考答案:象电子等实物粒子具有波动性被称作物质波。
物质波的波动性是和微粒行为的统计性联系在一起的。
对大量粒子而言，衍射强度（即波的强度）大的地方，粒子出现的数目就多，而衍射强度小的地方，粒子出现的数目就少。
对一个粒子而言，通过晶体到达底片的位置不能准确预测。
若将相同速度的粒子，在相同的条件下重复多次相同的实验，一定会在衍射强度大的地方出现的机会多，在衍射强度小的地方出现的机会少。
因此按照波恩物质波的统计解释，对于单个粒子，ψψ=ψ*2代表粒子的几率密度，在时刻t ，空间q 点附近体积元τd 内粒子的几率应为τd 2ψ；在整个空间找到一个粒子的几率应为12=ψ⎰τd 。
表示波函数具有归一性。
2 如何理解合格波函数的基本条件？参考答案合格波函数的基本条件是单值，连续和平方可积。
由于波函数2ψ代表概率密度的物理意义，所以就要求描述微观粒子运动状态的波函数首先必须是单值的，因为只有当波函数ψ在空间每一点只有一个值时，才能保证概率密度的单值性；至于连续的要求是由于粒子运动状态要符合Schrödinger 方程，该方程是二阶方程，就要求波函数具有连续性的特点；平方可积的是因为在整个空间中发现粒子的概率一定是100%，所以积分⎰τψψd *必为一个有限数。
3 如何理解态叠加原理？参考答案在经典理论中，一个波可由若干个波叠加组成。
这个合成的波含有原来若干波的各种成份（如各种不同的波长和频率）。
而在量子力学中，按波函数的统计解释，态叠加原理有更深刻的含义。
某一物理量Q 的对应不同本征值的本征态的叠加，使粒子部分地处于Q 1状态，部分地处于Q 2态，……。
各种态都有自己的权重（即成份）。
这就导致了在态叠加下测量结果的不确定性。
但量子力学可以计算出测量的平均值。
4 测不准原理的根源是什么？参考答案根源就在于微观粒子的波粒二象性。
21物质波及统计解释
2）电子衍射实验
单缝
双缝
三缝
四缝
电子的单缝、双缝、三缝和四缝衍射实验。 实验证实质子、中子、原子和分子等微观粒子都具 有波粒二象性，并满足德布罗意关系式。
例：设有m0=0.04Kg的子弹，速度为1000m/s，求其物 质波的波长。
h h 6.6310 解： P m v 0.041000 1.651035 m 1.651026 nm
波粒二象性
波函数及统计解释
2 P | | 1 1 P2 | 2 |2
二.用电子双缝干涉实验说明几率波的含义 • 只开上缝时 电子通过上缝的几率 • 只开下缝时 电子通过下缝的几率
•双缝齐开时 p12 p1 p2
p12 12
2
12 ?
p1
x
o
x
x
p12
p2
波粒二象性
德布罗意关系式：
h h 波长 p mv
注意 若 v c 则 若 v c则
频率
E mc h h
2
m m0
h h P 2mE
m m0 1 v 2 / c 2
德布罗意关系式可解释玻尔氢原子理论的定态条件.
物质波-实物粒子的波粒二象性
从德布罗意关系可以导出氢原子波尔理论中角动量 量子化条件. 两端固定的弦，若其长度 等于波长的整数倍可形成 稳定的驻波. 将弦弯曲成圆时
1 归一化因子 A
1 2x 例：给定( x) cos 2 a
x (0, a) 将其归一化
解:令以归一化波函数为 ( x), 设( x) c( x)
归一化：
1 2 a 2 2x ( x) dx 4 c 0 cos a dx x 1 2 a 1 cos 4a 1 2a c dx c 1 0 4 2 4 2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
物质波-实物粒子的波粒二象性
二.波函数的统计解释：概率波（1926年）
单电子双缝实验
玻恩获得1954 年
诺贝尔物理学奖
物质波-实物粒子的波粒二象性
二
物质波的统计解释
经典粒子：不被分割的整体，有确定位置和运动 轨道 ；经典的波：某种实际的物理量的空间分布作周 期性的变化. 二象性：将波和粒子两种对立的属性统一 到同一物体上 .
n 1,2,3,4, h 电子绕核运动其德布罗意波长为 mv
2π r n
h 角动量量子化条件 L mvr n 2π
2π rmv nh
物质波-实物粒子的波粒二象性
3.
电子的德布罗意波长
一原静止的电子被电场加速到速度u,(uc)。加速电 压为U，则速度为u的电子的德布罗意波波长为多大？ B 解：依守恒定律 m0 e U 加速电极
U 100 V , 0.123nm
：
U 1000 V , 0.039nm
与x射线的波长相当
4.
德布罗意波的实验验证
1）戴维逊--革末实验与汤姆逊实验
观测到 电 电子衍 子 射现象 束
电子波衍射图样 X射线衍射图样
实验原理
电子通过金薄膜的衍射实验
物质波-实物粒子的波粒二象性
波粒二象性是普遍的结论，宏观粒子也具有波动性； 普朗克常量 h 太小了，使得宏观物体的波长小得难 以测量，宏观物体只表现出粒子性。
34
物质波-实物粒子的波粒二象性
5. 德布罗意波应用举例：
扫描式电子显微鏡(SEM) 穿透式电子显微鏡(TEM) 扫描隧道显微鏡(STM) 原子力显微鏡(AFM) 磁力显微鏡(MFM)
一、 物质波 二、电子双缝干涉实验
三、物理对波函数的要求
物质波-实物粒子的波粒二象性
一 光的波粒二象性
《关于光的产生 和转化的一个启 发性观点》
物质波-实物粒子的波粒二象性
1. 光的波粒二象性
（1）波动性： （2）粒子性： 光子： 光的干涉和衍射.
E h （光电效应等） E pc
描述光的
物质波-实物粒子的波粒二象性
2. 德布罗意假设（1924 年）
德布罗意假设：不仅光具有波粒二象性，实 物粒子也具有波粒二象性 .
E h
p
h
德布罗意波：与粒子相联系的波称为德布罗 意波或者物质波 .
h h 波长 p mv
频率
E mc h h
2
物质波-实物粒子的波粒二象性
科学家使用STM观测物质的纳米结构
IBM公司苏黎世实验室的两位科学家宾尼希(G.Binnig) 和罗雷尔(H.Rohrer)发明了扫描隧道显微镜。与电子显 微镜的创制者E.Ruska(鲁斯卡)教授一起荣获1986年诺 贝尔物理奖。
物质波-实物粒子的波粒二象性
0 10
30
50
70
90
(nm)
硅晶体表面的STM扫描图象
K 发射电 子阴级
1 m0 v 2 eU 2 2eU 由此得： v m0
h h h 1 m0 v 2eUm0 2em0 U
物质波-实物粒子的波粒二象性
h h h 1 m0 v 2eUm0 2em0 U
1.226 U
nm
可获得电子在不同电压下的波长
U 10V , 0.39nm
2）电子衍射实验
单缝
双缝
三缝
四缝
电子的单缝、双缝、三缝和四缝衍射实验。 实验证实质子、中子、原子和分子等微观粒子都具 有波粒二象性，并满足德布罗意关系式。
例：设有m0=0.04Kg的子弹，速度为1000m/s，求其物 质波的波长。
h h 6.6310 解： P m v 0.041000 1.651035 m 1.651026 nm
物质波-实物粒子的波粒二象性
神经细胞的STM扫描图象
物质波-实物粒子的波粒二象性
搬运单个原子
CO分子小人
物质波-实物粒子的波粒二象性
量子围栏中的驻波 1993年克罗米等人用扫描隧道显微镜搬动48个Fe原子 到Cu表面上构成半径为7.13nm的圆柱形量子围栏。 并观察到了围栏内铜表面的电子产生的圆形驻波。
粒子性
E h h p c c E h 描述光的 h p 波动性
物质波-实物粒子的波粒二象性
法国物理学家德布罗意（Louis Victor de Broglie 1892 – 1987 ) 思想方法 自然界在许多方 面都是明显地对称的，他采用类 比的方法提出物质波的假设 . “整个世纪以来，在辐射理论上，比起波动的研 究方法来，是过于忽略了粒子的研究方法； 在实物 理论上，是否发生了相反的错误呢 ？ 是不是我们关 于‘粒子’的图象想得太多 ，而过分地忽略了波的 图象呢？”
第二章 波函数和 Schrö dinger 方程
本章要求
1 握态迭加原理 3 掌握薛定谔方程和量子力学的第二条基本假定
4 掌握定态、定态薛定谔方程、哈密顿算符、本征方程、本征
值和本征函数等概念
本 章 要 求：
5 掌握求解一维定态Schrö dinger 方程的基本步骤;
波粒二象性
•问题？
波函数及统计解释
如何描述微观粒子的波粒二象性？
E.SchrÖdinger提出可用一个波函数 (r , t )来描述 物质波，称为物质波的波函数。
如何体现波粒二象性的？
物质波是什么样的波？ M.Born通过与光的类比，从电子的波动性出发， 波函数的物理意义要从统计概率去解释。
6 了解能量量子化,束缚态,零点能,分立谱,连续谱,厄 密多项式等概念。
第二章 波函数和 Schrodinger 方程
2.1波函数的统计解释
态迭加原理 2.3 薛定谔方程 2.4 定态薛定谔方程 2.5 一维无限深势阱 2.6 线性谐振子
2.2
§2.1 物质波 波函数的统计解释
德布罗意关系式：
h h 波长 p mv
注意 若 v c 则 若 v c则
频率
E mc h h
2
m m0
h h P 2mE
m m0 1 v 2 / c 2
德布罗意关系式可解释玻尔氢原子理论的定态条件.
物质波-实物粒子的波粒二象性
从德布罗意关系可以导出氢原子波尔理论中角动量 量子化条件. 两端固定的弦，若其长度 等于波长的整数倍可形成 稳定的驻波. 将弦弯曲成圆时