宁夏石嘴山市高一下学期数学第二次月考试卷

高一下学期数学第二次月考试卷

高一下学期数学第二次月考试卷姓名:________ 班级:________ 成绩:________一、选择题（本大题共12小题，每小题5分，） (共12题；共60分)1. （5分）对有两个面互相平行，其余各面都是梯形的多面体，以下说法正确的是（）A . 棱柱B . 棱锥C . 棱台D . 一定不是棱柱、棱锥2. （5分） (2016高一下·平罗期末) 已知△ABC的平面直观图△A′B′C′是边长为2的正三角形，则△ABC 的面积为（）A . 2B .C . 2D . 43. （5分）三角形ABC中，,AB=3,BC=1 ，以边AB所在直线为旋转轴，其余各边旋转一周而形成的曲面所围成的几何体的体积为（）A .B .C . .D .4. （5分） (2016高三上·沙市模拟) 某几何体的三视图如图所示，则该几何体的体积为（）A .B .C .D .5. （5分）一个几何体的三视图如右图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，则该几何体的外接球的表面积为（）A .B .C .D .6. （5分） (2018高二上·万州期中) 已知水平放置的，按“斜二测画法”得到如图所示的直观图，其中，，那么原的面积是（）A .B .C .D .7. （5分）如图，正方体ABCD-A1B1C1D1的棱长为2，动点E、F在棱A1B1上，动点P，Q分别在棱AD，CD 上，若EF=1，A1E=x，DQ=y，DＰ＝ｚ（ｘ，ｙ，ｚ大于零），则四面体PEＦＱ的体积（）.A . 与ｘ，ｙ，ｚ都有关B . 与ｘ有关，与ｙ，ｚ无关C . 与ｚ有关，与ｘ，ｙ无关D . 与ｙ有关，与ｘ，ｚ无关8. （5分）棱长为a的正方体可任意摆放，则其在水平平面上投影面积的最大值为（）A . a2B . a2C . a2D . 2a29. （5分） (2016高一下·辽源期中) 已知{an}为等差数列，a3=7，a1+a7=10，Sn为其前n项和，则使得Sn 达到最大值的n等于（）A . 4B . 5C . 6D . 710. （5分）等差数列{an}中，已知前15项的和S15=90，则a8等于（）A .B . 12C .D . 611. （5分） (2019高三上·赤峰月考) 已知数列1，1，1，2，2，1，2，4，3，1，2，4，8，4，1，2，4，8，16，5，…，其中第一项是，第二项是1，接着两项为，，接着下一项是2，接着三项是，，，接着下一项是3，依此类推.记该数列的前项和为，则满足的最小的正整数的值为（）A . 65B . 67C . 75D . 7712. （5分） (2019高二上·上海月考) 设等差数列前项和为，且满足，，则、、、、中，最大项为（）A .B .C .D .二、填空题（本大题共4小题，每小题5分。

宁夏石嘴山市高一数学下学期期中试卷(含解析)

2016-2017学年宁夏石嘴山市高一（下）期中数学试卷一、选择题：1．一个人打靶时连续射击两次，事件“至少有一次中靶”的互斥事件是（）A．至多有一次中靶B．两次都中靶C．只有一次中靶 D．两次都不中靶2．已知点（﹣4，3）是角α终边上的一点，则sin（π﹣α）=（）A．B．C．D．3．下列式子中，不能化简为的是（）A．B．C．D．4．某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如图，其中甲班学生的平均分是85，乙班学生成绩的中位数是83．则x+y的值为（）A．7 B．8 C．9 D．105．下列语句：（1）两个有共同起点而且相等的向量，其终点必相同；（2）两个有共同终点的向量，一定是共线向量；（3）向量与向量是共线向量，则点A，B，C，D必在同一条直线上；（4）有向线段就是向量，向量就是有向线段．其中说法错误的个数是（）A．1 B．2 C．3 D．46．已知函数f（x）=sin（2x+φ）的图象关于直线对称，则φ可能是（）A．B．C．D．7．如图所示的程序框图，若输出的S=41，则判断框内应填入的条件是（）A．k＞3？B．k＞4？C．k＞5？D．k＞6？8．函数f（x）=cos（ωx+φ）的部分图象如图所示，则f（x）的单调递减区间为（）A．（kπ﹣，kπ+），k∈Z B．（2kπ﹣，2kπ+），k∈ZC．（k﹣，k﹣），k∈Z D．（2k﹣，2k+），k∈Z9．在函数①y=cos丨2x丨，②y=丨cosx丨，③y=cos（2x+）④y=tan（2x﹣）中，最小正周期为π的所有函数为（）A．①②③B．①③④C．②④ D．①③10．将函数的图象上各点的横坐标变为原来的π倍，将所得图象向右平移个单位，再向上平移1个单位，得到函数y=g（x）的图象，则函数y=g（x）的解析式是（）A．B．C．D．11．在区间[0，5]内随机选一个数，则它是不等式log2（x﹣1）＜1的解的概率是（）A．B．C．D．12．要得到函数的图象，只需将函数y=sin2x的图象（）A．向左平移个单位B．向右平移个单位C．向左平移个单位D．向右平移个单位二．填空题：13．将﹣300°化为弧度为．14．若sin（﹣α）=，则cos（+α）= ．15．满足的角α的集合为．16．关于函数f（x）=4sin（2x+）（x∈R），有下列命题：①由f（x1）=f（x2）=0可得x1﹣x2必是π的整数倍；②y=f（x）的表达式可改写为y=4cos（2x﹣）；③y=f（x）的图象关于点（﹣，0）对称；④y=f（x）的图象关于直线x=﹣对称．其中正确的命题的序号是．三.解答题（共70分）.17．（10分）（1）已知，求的值．（2）已知，求的值．18．（12分）某中学组织了一次高二文科学生数学学业水平模拟测试，学校从测试合格的男、女生中各随机抽取100人的成绩进行统计分析，分别制成了如图所示的男生和女生数学成绩的频率分布直方图．（Ⅰ）若所得分数大于等于80分认定为优秀，求男、女生优秀人数各有多少人？（Ⅱ）在（Ⅰ）中的优秀学生中用分层抽样的方法抽取5人，从这5人中任意选取2人，求至少有一名男生的概率．19．（12分）已知函数y=2sin（﹣2x），（1）求函数的周期；（2）求函数单调增区间；（3）求函数在[0，]上的值域．20．（12分）已知函数f（x）=Asin（ωx+φ）+B（ A＞0，ω＞0，，x∈R），在同一个周期内，当时，函数取最大值3，当时，函数取最小值﹣1，（1）求函数f（x）的解析式；（2）将f（x）的图象上所有点向左平移个单位，再将所得图象上所有点的横坐标变为原来的倍，得到g（x）的图象，讨论g（x）在上的单调性．21．（12分）某班同学利用国庆节进行社会实践，对[25，55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：（Ⅰ）补全频率分布直方图并求n、a、p的值；（Ⅱ）从年龄段在[40，50）的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动，其中选取2人作为领队，求选取的2名领队中恰有1人年龄在[40，45）岁的概率．22．（12分）已知函数f（x）=sin2x+acosx+a﹣，a∈R．（1）当a=1时，求函数f（x）的最大值最小值及相应的x的集合；（2）如果对于区间[0，]上的任意一个x，都有f（x）≤1成立，求a的取值范围．2016-2017学年宁夏石嘴山三中高一（下）期中数学试卷参考答案与试题解析一、选择题：1．一个人打靶时连续射击两次，事件“至少有一次中靶”的互斥事件是（）A．至多有一次中靶B．两次都中靶C．只有一次中靶 D．两次都不中靶【考点】C4：互斥事件与对立事件．【分析】利用互斥事件的概念求解．【解答】解：“至多有一次中靶”和“至少有一次中靶”，能够同时发生，故A错误；“两次都中靶”和“至少有一次中靶”，能够同时发生，故B错误；“只有一次中靶”和“至少有一次中靶”，能够同时发生，故C错误；“两次都不中靶”和“至少有一次中靶”，不能同时发生，故D正确．故选：D．【点评】本题考查互斥事件的判断，是基础题，解题时要熟练掌握互斥事件的概念．2．已知点（﹣4，3）是角α终边上的一点，则sin（π﹣α）=（）A．B．C．D．【考点】G9：任意角的三角函数的定义．【分析】由条件利用任意角的三角函数的定义，诱导公式，求得sin（π﹣α）的值．【解答】解：∵点（﹣4，3）是角α终边上的一点，∴x=﹣4，y=3，r=|OP|=5，∴sinα==，则sin（π﹣α）=sinα=，故选：A．【点评】本题主要考查任意角的三角函数的定义，诱导公式，属于基础题．3．下列式子中，不能化简为的是（）A．B．C．D．【考点】9B：向量加减混合运算及其几何意义．【分析】根据向量的加减的几何意义分别计算，再判断即可【解答】解：对于A： ++=+=，正确，对于B： ++﹣=﹣=，正确，对于C： +﹣=﹣=+，故不正确，对于D： +﹣=，正确，故选：C【点评】本题考查了向量的加减的几何意义，属于基础题4．某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如图，其中甲班学生的平均分是85，乙班学生成绩的中位数是83．则x+y的值为（）A．7 B．8 C．9 D．10【考点】BA：茎叶图；BB：众数、中位数、平均数．【分析】利用平均数求出x的值，中位数求出y的值，解答即可．【解答】解：由茎叶图可知甲班学生的总分为70×2+80×3+90×2+（8+9+5+x+0+6+2）=590+x，又甲班学生的平均分是85，总分又等于85×7=595．所以x=5乙班学生成绩的中位数是80+y=83，得y=3．∴x+y=8．故选B．【点评】本题考查数据的平均数公式与茎叶图，考查计算能力，基础题．5．下列语句：（1）两个有共同起点而且相等的向量，其终点必相同；（2）两个有共同终点的向量，一定是共线向量；（3）向量与向量是共线向量，则点A，B，C，D必在同一条直线上；（4）有向线段就是向量，向量就是有向线段．其中说法错误的个数是（）A．1 B．2 C．3 D．4【考点】91：向量的物理背景与概念．【分析】根据题意，结合向量的定义依次分析四个命题，综合即可得答案．【解答】解：根据题意，分析四个命题：对于①、相等向量是大小相等，方向相同的向量，故两个有共同起点而且相等的向量，其终点必相同，正确；对于②、共线向量是指方向相同或相反的向量，两个有共同终点的向量，其方向可能既不相同又不相反，故②错误；对于③、共线向量是指方向相同或相反的向量，向量与向量是共线向量，线段AB和CD平行或共线，故③错误；对于④、有向线段就是向量的表示形式，不能等同于向量，故④错误；四个命题中有3个错误，故选：C．【点评】本题考查向量的基本定义，关键是理解向量的定义．6．已知函数f（x）=sin（2x+φ）的图象关于直线对称，则φ可能是（）A．B．C．D．【考点】HK：由y=Asin（ωx+φ）的部分图象确定其解析式．【分析】由三角函数图象与性质可知，图象关于直线对称，则此时相位必为kπ+，k∈z，由此建立方程求出φ的表达式，再比对四个选项选出正确选项【解答】解：∵函数f（x）=sin（2x+φ）的图象关于直线对称∴2×+φ=kπ+，k∈z，∴φ=kπ+，k∈z，当k=0时，φ=，故选C．【点评】本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，正确解答本题，关键是了解函数对称轴方程的特征，及此时相位的特征，由此特征建立方程求参数，熟练掌握三角函数的性质是迅速，准确解三角函数相关的题的关键，7．如图所示的程序框图，若输出的S=41，则判断框内应填入的条件是（）A．k＞3？B．k＞4？C．k＞5？D．k＞6？【考点】EF：程序框图．【分析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是累加并输入S的值，条件框内的语句是决定是否结束循环，模拟执行程序即可得到答案．【解答】解：程序在运行过程中各变量值变化如下表：K S 是否继续循环循环前 1 0第一圈 2 2 是第二圈 3 7 是第三圈 4 18 是第四圈 5 41 否故退出循环的条件应为k＞4？故答案选：B．【点评】算法是新课程中的新增加的内容，也必然是新高考中的一个热点，应高度重视．程序填空也是重要的考试题型，这种题考试的重点有：①分支的条件②循环的条件③变量的赋值④变量的输出．其中前两点考试的概率更大．此种题型的易忽略点是：不能准确理解流程图的含义而导致错误．8．函数f（x）=cos（ωx+φ）的部分图象如图所示，则f（x）的单调递减区间为（）A．（kπ﹣，kπ+），k∈Z B．（2kπ﹣，2kπ+），k∈ZC．（k﹣，k﹣），k∈Z D．（2k﹣，2k+），k∈Z【考点】H7：余弦函数的图象．【分析】根据图象求出函数的解析式，结合三角函数的性质即可得到结论．【解答】解：从图象可以看出：图象过相邻的两个零点为（，0），（，0），可得：T=2×=2，∴ω==π，∴f（x）=cos（πx+φ），将点（，0）带入可得：cos（+φ）=0，令+φ=，可得φ=，∴f（x）=cos（πx+），由，单点递减（k∈Z），解得：2k﹣≤x≤2k+，k∈Z．故选D【点评】本题主要考查三角函数单调性的求解，利用图象求出三角函数的解析式是解决本题的关键．9．在函数①y=cos丨2x丨，②y=丨cosx丨，③y=cos（2x+）④y=tan（2x﹣）中，最小正周期为π的所有函数为（）A．①②③B．①③④C．②④ D．①③【考点】H1：三角函数的周期性及其求法．【分析】根据三角函数的周期性，求出各个函数的最小正周期，从而得出结论．【解答】解：∵函数①y=cos丨2x丨=cos2x，它的最小正周期为=π，②y=丨cosx丨的最小正周期为=π，③y=cos（2x+）的最小正周期为=π，④y=tan（2x﹣）的最小正周期为，故选：A．【点评】本题主要考查三角函数的周期性及求法，属于基础题．10．将函数的图象上各点的横坐标变为原来的π倍，将所得图象向右平移个单位，再向上平移1个单位，得到函数y=g（x）的图象，则函数y=g（x）的解析式是（）A．B．C．D．【考点】HJ：函数y=Asin（ωx+φ）的图象变换．【分析】由条件利用函数y=Asin （ωx+φ）的图象变换规律，得出结论．【解答】解将函数的图象上各点的横坐标变为原来的π倍，可得y=sin （+）的图象；将所得图象向右平移个单位，可得y=sin[（x ﹣）+]=sin 的图象；再向上平移1个单位，得到函数y=g （x ）=sin +1的图象，则函数y=g （x ）的解析式位 g （x ）=sin +1，故选：B ．【点评】本题主要考查函数y=Asin （ωx+φ）的图象变换规律，属于基础题．11．在区间[0，5]内随机选一个数，则它是不等式log 2（x ﹣1）＜1的解的概率是（）A ．B ．C ．D ．【考点】CF ：几何概型．【分析】由，得不等式log 2（x ﹣1）＜1的解集为（1，3），利用几何概型的概率计算公式可得答案【解答】解：由，得不等式log 2（x ﹣1）＜1的解集为（1，3），∴在区间[0，5]内随机选一个数，则它是不等式log 2（x ﹣1）＜1的解的概率是P=，故选：C ．【点评】本题考查了几何概型的概率计算公式，属于中档题．12．要得到函数的图象，只需将函数y=sin2x 的图象（）A ．向左平移个单位B ．向右平移个单位C ．向左平移个单位D ．向右平移个单位【考点】HJ ：函数y=Asin （ωx+φ）的图象变换．【分析】先根据诱导公式化简可得y=sin[2（x+）]，再根据左加右减的原则进行平移从而可得到答案．【解答】解：∵ =sin（2x+）=sin[2（x+）]，∴只需将函数y=sin2x的图象向左平移个单位即可得到函数的图象．故选：A．【点评】本题主要考查两角和与差的公式和三角函数的平移，三角函数平移时一定要遵循左加右减上加下减的原则．二．填空题：13．将﹣300°化为弧度为．【考点】G5：弧度与角度的互化．【分析】本题角度化为弧度，变换规则是度数乘以．【解答】解：﹣300°×=．故答案为：【点评】本题考查弧度与角度的互化，角度化为弧度用度数乘以，弧度化为角度用度数乘以，正确做对本题关键是熟练记忆转化的规则．14．若sin（﹣α）=，则cos（+α）= ．【考点】GO：运用诱导公式化简求值．【分析】直接利用诱导公式把要求的式子化为sin（﹣α），利用条件求得结果．【解答】解：∵sin（﹣α）=，∴cos（+α）=cos[﹣（﹣α）]=sin（﹣α）=，故答案为：．【点评】本题主要考查利用诱导公式进行化简求值，属于基础题．15．满足的角α的集合为{α|α，k∈Z} ．【考点】G9：任意角的三角函数的定义．【分析】直接利用余切线性质可得答案．【解答】解：∵，∴根据余切线可得：α，k∈Z．∴角α的集合为{α|α，k∈Z}．故答案为：{α|α，k∈Z}．【点评】本题考查余切线的运用，属于基本知识的考查．16．关于函数f（x）=4sin（2x+）（x∈R），有下列命题：①由f（x1）=f（x2）=0可得x1﹣x2必是π的整数倍；②y=f（x）的表达式可改写为y=4cos（2x﹣）；③y=f（x）的图象关于点（﹣，0）对称；④y=f（x）的图象关于直线x=﹣对称．其中正确的命题的序号是②③．【考点】GL：三角函数中的恒等变换应用；H6：正弦函数的对称性．【分析】根据函数求出最小正周期，可知①错；利用诱导公式化简②，判断正误；求出函数的对称中心判定③；对称直线方程判断④的正误；即可得到解答．【解答】解：①函数f（x）=4sin的最小正周期T=π，由相邻两个零点的横坐标间的距离是=知①错．②f（x）=4sin（2x+）=4cos（﹣2x﹣）=4cos（2x+﹣）=4cos（2x﹣）③f（x）=4sin（2x+）的对称点满足（x，0）2x+=kπ，x=（） k∈Z（﹣，0）满足条件④f（x）=4sin（2x+）的对称直线满足2x+=（k+）π；x=（k+）x=﹣不满足故答案为：②③【点评】本题考查三角函数的周期性及其求法，诱导公式的利用，以及正弦函数的对称性问题，属于基础题．三.解答题（共70分）.17．（10分）（2017春•大武口区校级期中）（1）已知，求的值．（2）已知，求的值．【考点】GI：三角函数的化简求值．【分析】（1）由已知利用诱导公式求出sinθ，再由三角函数的诱导公式解析化简求值；（2）由已知化弦为切求出tanα，再利用商的关系化弦为切求得的值．【解答】解：（1）由，得sin．∴==；（2）由，得，得tan．∴===．【点评】本题考查三角函数的化简求值，考查了同角三角函数基本关系式的应用，利用“齐次式”化弦为切是关键，是中档题．18．（12分）（2017•济宁一模）某中学组织了一次高二文科学生数学学业水平模拟测试，学校从测试合格的男、女生中各随机抽取100人的成绩进行统计分析，分别制成了如图所示的男生和女生数学成绩的频率分布直方图．（Ⅰ）若所得分数大于等于80分认定为优秀，求男、女生优秀人数各有多少人？（Ⅱ）在（Ⅰ）中的优秀学生中用分层抽样的方法抽取5人，从这5人中任意选取2人，求至少有一名男生的概率．【考点】CC：列举法计算基本事件数及事件发生的概率；B8：频率分布直方图．【分析】（Ⅰ）根据频率分布直方图求出男、女生优秀人数即可；（Ⅱ）求出样本中的男生和女生的人数，求出所有的基本事件以及满足条件的基本事件的个数，从而求出满足条件的概率即可．【解答】解：（Ⅰ）由题意可得，男生优秀人数为100×（0.01+0.02）×10=30人，女生优秀人数为100×（0.015+0.03）×10=45人．（Ⅱ）因为样本容量与总体中的个体数的比是，所以样本中包含男生人数为人，女生人数为人，设两名男生为A1，A2，三名女生为B1，B2，B3，则从5人中任意选取2人构成的所有基本事件为：{A1，A2}，{A1，B1}，{A1，B2}，{A1，B3}，{A2，B1}，{A2，B2}，{A2，B3}，{B1，B2}，{B1，B3}，{B2，B3}共10个，每个样本被抽到的机会均等，因此这些基本事件的出现是等可能的．记事件C：“选取的2人中至少有一名男生”，则事件C包含的基本事件有：{A1，A2}，{A1，B1}，{A1，B2}，{A1，B3}，{A2，B1}，{A2，B2}，{A2，B3}共7个，所以，即选取的2人中至少有一名男生的概率为．【点评】本题考查了频率分布问题，考查条件概率问题，是一道中档题．19．（12分）（2017春•大武口区校级期中）已知函数y=2sin（﹣2x），（1）求函数的周期；（2）求函数单调增区间；（3）求函数在[0，]上的值域．【考点】H2：正弦函数的图象．【分析】（1）化函数为y=﹣2sin（2x﹣），求出函数f（x）的周期T=；（2）由正弦函数的单调性求出函数f（x）的单调增区间；（3）由x∈[0，]求得函数f（x）的值域即可．【解答】解：（1）函数y=2sin（﹣2x）=﹣2sin（2x﹣），∴函数f（x）的周期为T===π；（2）由+2kπ≤2x﹣≤+2kπ，k∈Z；+kπ≤x≤+kπ，k∈Z；∴函数f（x）单调增区间为[+kπ， +kπ]，k∈Z；（3）由x∈[0，]，得2x∈[0，π]，∴2x﹣∈[﹣，]，∴sin（2x﹣）∈[﹣，1]，∴﹣2sin（2x﹣）∈[﹣2，]，∴函数f（x）在[0，]上的值域是[﹣2，]．【点评】本题考查了正弦函数的图象与性质的应用问题，是中档题．20．（12分）（2017春•大武口区校级期中）已知函数f（x）=Asin（ωx+φ）+B（ A＞0，ω＞0，，x∈R），在同一个周期内，当时，函数取最大值3，当时，函数取最小值﹣1，（1）求函数f（x）的解析式；（2）将f（x）的图象上所有点向左平移个单位，再将所得图象上所有点的横坐标变为原来的倍，得到g（x）的图象，讨论g（x）在上的单调性．【考点】HJ：函数y=Asin（ωx+φ）的图象变换；HK：由y=Asin（ωx+φ）的部分图象确定其解析式．【分析】（1）根据最值计算A，B，根据周期计算ω，根据f（）=3计算φ；（2）根据函数图象变换得出g（x）的解析式，求出g（x）的单调区间即可．【解答】解：（1）由题意得，∴．f（x）的周期T=2（）=．∴=，即ω=3．∵f（）=2sin（+φ）+1=3，∴+φ=+2kπ，∴φ=﹣+2kπ，k∈Z，∵|φ|＜，∴φ=﹣．∴f（x）=2sin（3x﹣）+1．（2）g（x）=2sin（2x+）+1，令﹣+2kπ≤2x+≤+2kπ，解得﹣+kπ≤x≤+kπ，k∈Z．[﹣+kπ， +kπ]∩[﹣，]=[﹣π，]，∴g （x ）在[﹣π，]上单调递增，在[﹣，﹣]，[，]上单调递减．【点评】本题考查了三角函数的图象与性质，函数图象变换，属于中档题．21．（12分）（2016•锦州二模）某班同学利用国庆节进行社会实践，对[25，55]岁的人群随机抽取n 人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：（Ⅰ）补全频率分布直方图并求n 、a 、p 的值；（Ⅱ）从年龄段在[40，50）的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动，其中选取2人作为领队，求选取的2名领队中恰有1人年龄在[40，45）岁的概率．【考点】BF ：随机抽样和样本估计总体的实际应用；B8：频率分布直方图．【分析】（I ）根据频率分步直方图的面积是这组数据的频率，做出频率，除以组距得到高，画出频率分步直方图的剩余部分，根据频率，频数和样本容量之间的关系，做出n 、a 、p 的值．（II ）根据分层抽样方法做出两个部分的人数，列举出所有试验发生包含的事件和满足条件的事件，根据等可能事件的概率公式，得到结果．【解答】解：（Ⅰ）∵第二组的频率为1﹣（0.04+0.04+0.03+0.02+0.01）×5=0.3，∴高为．频率直方图如下：第一组的人数为，频率为0.04×5=0.2，∴．由题可知，第二组的频率为0.3，∴第二组的人数为1000×0.3=300，∴．第四组的频率为0.03×5=0.15，∴第四组的人数为1000×0.15=150，∴a=150×0.4=60．（Ⅱ）∵[40，45）岁年龄段的“低碳族”与[45，50）岁年龄段的“低碳族”的比值为60：30=2：1，所以采用分层抽样法抽取6人，[40，45）岁中有4人，[45，50）岁中有2人．设[40，45）岁中的4人为a、b、c、d，[45，50）岁中的2人为m、n，则选取2人作为领队的有（a，b）、（a，c）、（a，d）、（a，m）、（a，n）、（b，c）、（b，d）、（b，m）、（b，n）、（c，d）、（c，m）、（c，n）、（d，m）、（d，n）、（m，n），共15种；其中恰有1人年龄在[40，45）岁的有（a，m）、（a，n）、（b，m）、（b，n）、（c，m）、（c，n）、（d，m）、（d，n），共8种．∴选取的2名领队中恰有1人年龄在[40，45）岁的概率为．【点评】本题考查频率分步直方图，考查频数，频率和样本容量之间的关系，考查等可能事件的概率，考查利用列举法来得到题目要求的事件数，本题是一个概率与统计的综合题目．22．（12分）（2017春•大武口区校级期中）已知函数f（x）=sin2x+acosx+a﹣，a∈R．（1）当a=1时，求函数f（x）的最大值最小值及相应的x的集合；（2）如果对于区间[0，]上的任意一个x，都有f（x）≤1成立，求a的取值范围．【考点】GL：三角函数中的恒等变换应用；H2：正弦函数的图象．【分析】可得f（x）=﹣cos2x+acosx+﹣，令t=cosx，所以f（x）=﹣t2+at+﹣，（1）当a=1时，f（x）=﹣t2+t+=﹣（t﹣）2+，即可求解（2）f（x）=﹣（cosx﹣2+在[0，]上，cosx∈[0，1]，分以下情况求解①，②，③，【解答】解：化简可得f（x）=﹣cos2x+acosx+﹣，令t=cosx，所以f（x）=﹣t2+at+﹣，（1）当a=1时，f（x）=﹣t2+t+=﹣（t﹣）2+，因为x∈R，所以t∈[﹣1，1]，关于t的二次函数开口向下，对称轴为t=，故当t=时，函数取最大值f（x）max=，此时cosx=，x的集合为{x|x=2kπ±，k∈Z}当t=﹣1时，函数取最小值f（x）min=﹣，此时cosx=﹣1，x的集合为{x|x=2kπ+π，k ∈Z}（2）f（x）=﹣（cosx﹣）2+，在[0，]上，cosx∈[0，1]，当时，f （x ）max =，解得﹣4，则0；当时，f （x ）max =，解得a ，则a ≤0；当，时，f （x ）max =a+，解得a，无解．综上，a 的取值范围时（﹣]．【点评】本题考查了三角恒等变形、含参数二次函数的最值问题，考查了分类讨论思想，属于中档题．。

宁夏高一数学下学期第二次月考试卷(含解析)

2016-2017学年宁夏高一（下）第二次月考数学试卷一、选择题（本题共12小题，每小题4分）1．已知角α的终边经过点P（4，﹣3），那么cosα﹣sinα的值是（）A．B．﹣ C．D．2．已知，则的坐标是（）A．（6，﹣5）B．（6，7）C．（6，1）D．（6，﹣1）3．已知，则cos（π+α）的值是（）A．B．﹣ C．D．﹣4．下列各组平面向量中，可以作为基底的是（）A． 1=（0，0），2=（1，﹣2）B． 1=（﹣1，2），2=（5，7）C． 1=（3，5），2=（6，10）D． 1=（2，﹣3），2=（，﹣）5．如图，在平行四边形ABCD中，下列结论中错误的是（）A． =B． +=C． +=D． +=6．在△ABC中，BC=5，AC=8，C=60°，则=（）A．20 B．﹣20 C．D．7．要得到y=3sin2x的图象，只需将y=3sin（2x+）的图象（）A．向右平移个单位B．向左平移个单位C．向左平移个单位D．向右平移个单位8．如图，D，E，F分别是△ABC的边AB，BC，CA的中点，则（）A．B．C．D．9．下列命题中：①若与互为相反向量，则；②若，则；③若，则或；④若，且，则．其中假命题的个数为（）A．1 B．2 C．3 D．410．已知向量与的夹角为120°，，则等于（）A．5 B．4 C．3 D．111．已知函数，x∈R，以下结论：①f（x）的最小正周期是π；②f（x）的图象关于点对称；③f（x）的图象关于直线对称；④f（x）在区间上是增函数；其中正确命题的个数是（）A．4 B．3 C．2 D．112．已知函数y=Asin（ωx+ϕ）（A＞0，ω＞0，|φ|＜），在同一周期内，时取得最大值，时取得最小值﹣，则该函数解析式为（）A． B．C．D．二、填空题（每小题4分，共16分）13．求值：sin750°+cos（﹣660°）+tan（﹣135°）．14．函数的定义域是．15．已知，，且∥，则的坐标为．16．已知，，且，则在方向上的投影为．三、解答题（本题共6道大题，共56分）17．已知=（1，2），=（﹣3，2），当k= 时，（1）k+与﹣3垂直；当k= 时，（2）k+与﹣3平行．18．已知，是同一平面内两个不共线的向量，（1）如果=+， =2﹣， =4+，求证A、B、D三点共线；（2）试确定实数k的值，使和共线．19．已知，是同一平面内两个单位向量，其夹角为60°，如果=2+， =﹣3+2．（1）求（2）求与的夹角．20．已知，（1）求tanα；（2）求sin2α+sinαcosα的值．21．在△ABC中，M是线段AB的中点，，BN与CM相交于点E，设，，（1）用基底，表示和；（2）用基底，表示．22．已知函数（1）求f（x）的单调递增区间；（2）若x∈[0，2π]，求f（x）的值域．2016-2017学年宁夏育才中学孔德校区高一（下）第二次月考数学试卷参考答案与试题解析一、选择题（本题共12小题，每小题4分）1．已知角α的终边经过点P（4，﹣3），那么cosα﹣sinα的值是（）A．B．﹣ C．D．【考点】G9：任意角的三角函数的定义．【分析】由条件利用任意角的三角函数的定义，求得sinα和cosα的值，可得cosα﹣sinα的值．【解答】解：由于角α的终边经过点P（4，﹣3），则x=4、y=﹣3、r=|OP|=5，∴sinα==﹣，cosα==，∴cosα﹣sinα=，故选：D．2．已知，则的坐标是（）A．（6，﹣5）B．（6，7）C．（6，1）D．（6，﹣1）【考点】9J：平面向量的坐标运算．【分析】利用向量坐标运算性质即可得出．【解答】解： =（6，4）﹣（0，﹣3）=（6，7），故选：B．3．已知，则cos（π+α）的值是（）A．B．﹣ C．D．﹣【考点】GO：运用诱导公式化简求值．【分析】由条件利用诱导公式进行化简所给的式子，可得结果．【解答】解：∵已知=﹣cosα，则cos（π+α）=﹣cosα=，故选：A．4．下列各组平面向量中，可以作为基底的是（）A． 1=（0，0），2=（1，﹣2）B． 1=（﹣1，2），2=（5，7）C． 1=（3，5），2=（6，10）D． 1=（2，﹣3），2=（，﹣）【考点】9H：平面向量的基本定理及其意义．【分析】不共线的两个向量才可作为基底，从而判断每个选项的两个向量是否共线，这样即可找出能作为基底的一组向量．【解答】解：A.，∴共线，不能作为基底；B．﹣1×7﹣2×5≠0；∴不共线，可以作为基底；C.；∴共线，不能作为基底；D.；∴共线，不能作为基底．故选B．5．如图，在平行四边形ABCD中，下列结论中错误的是（）A． =B． +=C． +=D． +=【考点】9B：向量加减混合运算及其几何意义．【分析】根据向量加法的平行四边形法则以及平行四边形的性质解答即可．【解答】解：由平行四边形的性质，可得，选项A正确；由向量加法的平行四边形法则，可得，选项B正确；∵，∴选项D正确；∵，∴选项C错误．故选：C．6．在△ABC中，BC=5，AC=8，C=60°，则=（）A．20 B．﹣20 C．D．【考点】9R：平面向量数量积的运算．【分析】利用已知条件，通过向量的数量积求解即可．【解答】解：在△ABC中，BC=5，AC=8，C=60°，则==5×=﹣20．故选：B．7．要得到y=3sin2x的图象，只需将y=3sin（2x+）的图象（）A．向右平移个单位B．向左平移个单位C．向左平移个单位D．向右平移个单位【考点】HJ：函数y=Asin（ωx+φ）的图象变换．【分析】根据两个函数之间的关系即可得到结论．【解答】解：∵y=3sin（2x+）=3sin2（x+），∴y=3sin（2x+）的向右平移个单位，即可得到y=3sin2x的图象，故选：A8．如图，D，E，F分别是△ABC的边AB，BC，CA的中点，则（）A．B．C．D．【考点】9B：向量加减混合运算及其几何意义．【分析】根据向量的四则运算进行求解即可．【解答】解：∵D，E，F分别是△ABC的边AB，BC，CA的中点，∴=， =， =，则++=++=（++）=，故选：A9．下列命题中：①若与互为相反向量，则；②若，则；③若，则或；④若，且，则．其中假命题的个数为（）A．1 B．2 C．3 D．4【考点】2K：命题的真假判断与应用．【分析】由相反向量的定义，模相等方向相反的向量称为相反向量，即可判断①；由单位向量的定义，即可判断②；由向量垂直的条件：数量积为0，即可判断③；由条件可得（﹣）•=0，则或（﹣）⊥，即可判断④．【解答】解：①由相反向量的定义，可得：若与互为相反向量，则，故①正确；②若，即为单位向量，故②错误；③若，则||•||cos＜，＞=0，可得或或⊥，故③错误；④若，且，则（﹣）•=0，则或（﹣）⊥，故④错误．故选：C．10．已知向量与的夹角为120°，，则等于（）A．5 B．4 C．3 D．1【考点】9S：数量积表示两个向量的夹角；93：向量的模．【分析】本题是对向量数量积的考查，根据两个向量的夹角和模之间的关系，用数量积列出等式，再根据和的模两边平方，联立解题，注意要求的结果非负，舍去不合题意的即可．【解答】解：∵向量与的夹角为120°，，∴，∵，∴，∴=﹣1（舍去）或=4，故选B．11．已知函数，x∈R，以下结论：①f（x）的最小正周期是π；②f（x）的图象关于点对称；③f（x）的图象关于直线对称；④f（x）在区间上是增函数；其中正确命题的个数是（）A．4 B．3 C．2 D．1【考点】2K：命题的真假判断与应用．【分析】运用正弦型函数的周期公式，即可判断①；由正弦函数的对称中心的特点，计算即可判断②；由正弦函数的对称轴的特点，计算即可判断③；由正弦函数的增区间，解不等式即可判断④．【解答】解：函数，①f（x）的最小正周期是T==π，故①对；②由f（﹣）=2sin（﹣+）=0，可得f（x）的图象关于点对称，故②对；③由f（）=2sin（+）=，不为最值，f（x）的图象不关于直线对称，故③错；④由2kπ﹣≤2x+≤2kπ+，k∈Z，可得kπ﹣≤x≤kπ+，k∈Z，则f（x）在区间（0，）递增，在（，）递减，故④错．故选：C．12．已知函数y=Asin（ωx+ϕ）（A＞0，ω＞0，|φ|＜），在同一周期内，时取得最大值，时取得最小值﹣，则该函数解析式为（）A． B．C．D．【考点】HK：由y=Asin（ωx+φ）的部分图象确定其解析式．【分析】由函数的图象的顶点坐标求出A、φ，由周期求出ω，可得函数的解析式．【解答】解：函数y=Asin（ωx+ϕ）（A＞0，ω＞0，|φ|＜），在同一周期内，时取得最大值，时取得最小值﹣，∴A=， =﹣，∴ω=3．再根据3•+φ=2kπ+，k∈Z，∴φ=，故函数的解析式为 y=sin（3x+），故选：B．二、填空题（每小题4分，共16分）13．求值：sin750°+cos（﹣660°）+tan（﹣135°）．【考点】GO：运用诱导公式化简求值．【分析】利用诱导公式可得sin750°+cos（﹣660°）+tan（﹣135°）=sin30°+cos60°+tan45°，从而可得答案．【解答】解：sin750°+cos（﹣660°）+tan（﹣135°）=sin（2×360°+30°）+cos（﹣2×36°+60°）+tan（﹣180°+45°）=sin30°+cos60°+tan45°=++1=2．14．函数的定义域是．【考点】33：函数的定义域及其求法．【分析】函数的定义域满足：2x+≠k，k∈Z，由此能求出函数的定义域．【解答】解：函数的定义域满足：2x+≠k，k∈Z，解得x≠+，k∈Z，∴函数的定义域是．故答案为：．15．已知，，且∥，则的坐标为（2，﹣4）或（﹣2，4）．【考点】96：平行向量与共线向量．【分析】设=（x，y），由，，且∥，利用向量的模的定义和向量平行的条件，列出方程组，能求出的坐标．【解答】解：设=（x，y），∵，，且∥，∴，解得或，∴=（2，﹣4）或=（﹣2，4）．故答案为：（2，﹣4）或（﹣2，4）．16．已知，，且，则在方向上的投影为﹣2 ．【考点】9R：平面向量数量积的运算．【分析】根据平面向量数量积公式求出•的值，再求在方向上的投影大小．【解答】解：，，且，∴4﹣4•﹣3=4×42﹣4•﹣3×32=61，解得•=﹣6，∴在方向上的投影为：||cosθ===﹣2．故答案为：﹣2．三、解答题（本题共6道大题，共56分）17．已知=（1，2），=（﹣3，2），当k= 19 时，（1）k+与﹣3垂直；当k= 时，（2）k+与﹣3平行．【考点】9T：数量积判断两个平面向量的垂直关系．【分析】由向量的坐标运算可得k+=（k﹣3，2k+2），﹣3=（10，﹣4），由垂直和平行关系分别可得k的方程，解方程可得答案．【解答】解：（1）∵=（1，2），=（﹣3，2），∴k+=（k﹣3，2k+2），﹣3=（10，﹣4）∵k+与﹣3垂直，∴10（k﹣3）﹣4（2k+2）=0，解得k=19；（2）由（1）知k+=（k﹣3，2k+2），﹣3=（10，﹣4）∵k+与﹣3平行，∴﹣4（k﹣3）=10（2k+2），解得k=﹣故答案为：19；．18．已知，是同一平面内两个不共线的向量，（1）如果=+， =2﹣， =4+，求证A、B、D三点共线；（2）试确定实数k的值，使和共线．【考点】96：平行向量与共线向量．【分析】（1）证明，共线即可；（2）利用向量共线定理和平面向量基本定理即可得出．【解答】（1）证明：∵ =，∴与共线，又与有公共点B，∴A，B，D三点共线；（2）解：∵若使和共线．∴存在实数λ，使得=λ（）成立，∴．∵，是同一平面内两个不共线的向量，∴，解得．∴实数k的值是±2．19．已知，是同一平面内两个单位向量，其夹角为60°，如果=2+， =﹣3+2．（1）求（2）求与的夹角．【考点】9R：平面向量数量积的运算；9S：数量积表示两个向量的夹角．【分析】（1）由已知=2+， =﹣3+2，直接展开得答案；（2）求出、的值，结合（1）中求出的，代入数量积求夹角公式得答案．【解答】解：（1）由已知得，cos＜＞=．∵=2+， =﹣3+2，∴=（2+）•（﹣3+2）=﹣6=﹣6+1×+2=；（2）==．=．设与的夹角为θ（0≤θ≤180°），则c osθ==．∴θ=120°．20．已知，（1）求tanα；（2）求sin2α+sinαcosα的值．【考点】GI：三角函数的化简求值．【分析】把已知等式两边平方，可得α∈（），求出sinα﹣cosα的值，与原式联立求得sinα、cosα的值．（1）直接由商的关系求得ta nα；（2）把分母中的“1”用平方关系代替，化弦为切求解．【解答】解：由，得，∴2sinαcosα=．∵0＜α＜π，∴α∈（），则sinα＞0，cosα＜0．则sinα﹣cosα==．联立，解得．（1）tan=；（2）sin2α+sinαcosα====．21．在△ABC中，M是线段AB的中点，，BN与CM相交于点E，设，，（1）用基底，表示和；（2）用基底，表示．【考点】9H：平面向量的基本定理及其意义．【分析】（1）根据向量加法的三角形法则表示；（2）设=x﹣， =y，用两种方法表示出，列方程组得出x，y即可表示出．【解答】解：（1）∵M是线段AB的中点，，∴=， =，∴=﹣+=﹣+，=﹣+=．（2）设=x﹣， =y，则==（）+x，又==y+（），∴，解得，∴=．22．已知函数（1）求f（x）的单调递增区间；（2）若x∈[0，2π]，求f（x）的值域．【考点】H5：正弦函数的单调性；HW：三角函数的最值．【分析】（1）利用正弦函数的单调性，求得f（x）的单调递增区间．（2）利用正弦函数的定义域和值域，求得f（x）的值域．【解答】解：（1）对于函数，令2kπ﹣≤+≤2kπ+，求得4kπ﹣≤x≤4kπ+，可得f（x）的单调递增区间为[4kπ﹣，4kπ+]，k∈Z．（2）当x∈[0，2π]， +∈[，]，∴sin（+）∈[﹣，1]，∴ sin （+）∈[﹣1，]，∴f（x）∈[0， +1]．。

高一下学期第二次月考数学试题(含答案)

答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读题，结合平时课堂上所学的知识，解答难题；一定要镇定，不能因此慌了手脚，影响下面的答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的小朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！第二学期第二次月考高一年级数学试题满分150 时间：120分钟一、单项选择题（每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的）1. 以3i 2-的虚部为实部，以23i 2i +的实部为虚部的复数是（）A. 33i - B. 3i + C. 22i -+ D. 22i+【答案】A 【解析】【分析】确定所求复数的实部和虚部，即可得解.【详解】复数3i 2-的虚部为3，复数23i 2i 32i +=-+的实部为3-，故所求复数为33i -，故选：A.2. 下列命题中，正确的是（）A. 有两个侧面是矩形的棱柱是直棱柱B. 侧面都是等腰三角形的棱锥是正棱锥C. 侧面都是矩形的直四棱柱是长方体D. 底面为正多边形，且有相邻两个侧面与底面垂直的棱柱是正棱柱【答案】D 【解析】【分析】根据直棱柱，正棱锥，长方体，正棱柱的结构特征及定义逐一判断即可.【详解】解：对于A ，因为侧棱都垂直于底面的棱柱叫直棱柱，当两个侧面是矩形时，不能保证所有侧棱都垂直于底面，这样的棱柱不是直棱柱，故A 错误；对于B ，侧棱都相等且底面是正多边形的棱锥叫做正棱锥，故B 错误；对于C ，当底面不是矩形时，这样的四棱柱不是长方体，故C 错误；对于D ，因为棱柱的侧棱平行，则相邻两个侧面与底面垂直，可得所有的侧棱与底面都垂直，所以底面为正多边形，且有相邻两个侧面与底面垂直的棱柱是正棱柱，故D 正确.故选：D .3. 已知ABC V 中，4,30a b A ===°，则B 等于（）A. 60°或120°B. 30°或150°C. 60°D. 30°【答案】A 【解析】【分析】直接利用正弦定理即可得解.【详解】解：ABC V 中，因为4,30a b A ===°，所以B A >，因为sin sin a bA B=，所以sin sin b A B a ==，又0180A <<°°，所以60B =°或120°.故选：A .4. 若复数z 满足()212i z i +=-，则复数z 所对应的点位于A. 第一象限 B. 第二象限C. 第三象限D. 第四象限【答案】D 【解析】【详解】解：由题意可得：122iz i -====+ ,据此可知：复数z 所对应的点位于第四象限.本题选择D 选项.5. 已知平面向量,a b rr 满足3,2a b ==r r ，a r 与b r 的夹角为60°,若()a mb a -^r r r ,则实数m 的值为（）A. 1 B.32C. 2D. 3【答案】D 【解析】【详解】,a b r r的夹角为60o ，且3,2a b ==r r ，则·32cos 603a b =´´=o r r ，又由()a mb a -^r r r ，可得()·0a mb a -=r r r ，变形可得2·a ma b=r r r ，即93m =´ ，解可得3m = ，故选D.6. ABC D 内角A ，B ，C 的对边分别为a ，b ，c ，已知2b =，6B p=，4C p=，则ABC D 的面积的为A. 2+B.1+C. 2-D.1-【答案】B 【解析】详解】试题分析：根据正弦定理，，解得，，并且，所以考点：1．正弦定理；2．面积公式．7. 已知是球的球面上两点,,为该球面上的动点.若三棱锥体积的最大值为36,则球的表面积为（）A. 36πB. 64πC. 144πD. 256π【答案】C 【解析】【详解】如图所示，当点C 位于垂直于面AOB 的直径端点时，三棱锥O ABC -的体积最大，设球O 的半径为R ，此时2311136326O ABC C AOB V V R R R --==´´==，故6R =，则球O 的表面积为24144S R p p ==，故选C ．考点：外接球表面积和椎体的体积．8. 向量()1,1a =-r ，且向量a r与向量2a b +r r 方向相同，则a b ×r r 的取值范围是（）A. ()1,1- B. ()1,-+µ【C. ()1,+µD. (),1-µ【答案】B 【解析】【分析】根据共线向量定理，结合条件列出方程，即可得到结果.【详解】因向量a r与向量2a b +r r 方向相同，则存在实数,0l l >，使得()2a a bl =+r r r 即()12a bl l -=r r所以12b a l l -=r r，因为()1,1a =-r ，所以22a =r 所以2112ab a l ll l --×=×=r r r 因为0l >，所以1a b ×>-r r故选:B .二、多项选择题：每小题5分，共20分.在每小题给出的选项中有多项符合题目要求，全部选对的得5分，部分选对得2分，有选错的得0分）9. 在ABC V 中，222sin sin sin sin sin A B C B C +-≤，则A 可以是（）A.π12B.6p C.π3D.2π3【答案】ABC 【解析】【分析】利用正弦定理结合余弦定理可求得cos A 的取值范围，可求得角A 的取值范围，即可得出合适的选项.【详解】在ABC V 中，设内角A 、B 、C 的对边分别为a 、b 、c ，因为222sin sin sin sin sin A B C B C +-≤，可得222b c a bc +-³，则2221cos 22b c a A bc +-=³，0πA <<Q ，π03A \<£.故选：ABC.10. 下列命题中错误的有（）A. 若平面内有四点A B C D 、、、，则必有AC BD BC AD +=+uuu r uuu r uuu r uuu r；为B. 若e r为单位向量，且//a e r r ，则a a e =r r r ；C. 3a a a a =r r r r g g ；D. 若a r 与b r 共线，又b r 与c r 共线，则a r 与c r必共线；【答案】BCD 【解析】【分析】利用平面向量的减法化简判断选项A ；由向量共线以及单位向量的性质判断选项B ；由数量积的运算判断选项C ，由向量共线以及零向量的性质判断选项D ．【详解】对于A ，AC BD BC AD -=-uuu r uu uuu r Q u r uuu r ，AC BD BC AD \+=+uuu r uuu r uuu r uuu r，正确；对于B ，e r为单位向量，且//a e r r ，则a a e =±r r r ，错误；对于C ，23a a a a a a =¹r r r r r r g g g ，错误；对于D ，若0b =r r ，则a r 与b r 共线，b r 与c r 共线，而a r 与c r不确定，错误；故选：BCD11. 在四棱锥P ABCD -中，已知PA ^底面ABCD ，且底面ABCD 为矩形，则下列结论中正确的是（）A. 平面PAB ^平面PADB. 平面PAB ^平面PBCC. 平面PBC ^平面PCDD. 平面PCD ^平面PAD【答案】ABD 【解析】【分析】根据线面垂直的判定定理和面面垂直的判定定理，逐项判定，即可求解.【详解】对于A 中，由已知PA ^底面ABCD ，且底面ABCD 为矩形，所以,PA AB AB AD ^^，且PA AD A Ç=,,PA AD Ì平面PAD ，所以AB ^平面PAD ，又由AB Ì平面PAB ，所以平面PAB ^平面PAD ，所以A 正确；对于B 中，由已知PA ^底面ABCD ，且底面ABCD 为矩形，所以,PA BC AB BC ^^，且PA AB A =I ,,PA AB Ì平面PAB ，所以BC ^平面PAB ，又由BC Ì平面PBC ，所以平面PAB ^平面PBC ，所以B 正确；对于C 中，假设平面PBC ^平面PCD ，过点B 作BE PC ^，可得BE ^平面PCD ，因为CD Ì平面PCD ，所以BE CD ^，又由CD BC ^，且BE BC B =I ，所以CD ^平面PBC ，可得CD PC ^，这与CD PD ^矛盾，所以平面PBC 与平面PCD 不垂直，所以C 不正确；对于D 中，由已知PA ^底面ABCD ，且底面ABCD 为矩形，所以,PA CD AD CD ^^，且PA AD A Ç=,,PA AD Ì平面PAD ，所以CD ^平面PAD ，又由CD Ì平面PCD ，所以平面PCD ^平面PAD ，所以D 正确.故选：ABD.12. 已知函数()sin f x x x =,则下列命题正确的是（）A. 函数π()(0,)2f x x éùÎêúëû的单调递增区间是π0,6éùêúëû；B. 函数()f x 的图象关于点π(,0)6-对称；C. 函数()f x 的图象向左平移(0)m m >个单位长度后，所得的图象关于y 轴对称，则m 的最小值是π6；D. 若实数m 使得方程()f x m =在[]02π，上恰好有三个实数解1x ，2x ，3x ，则1237π3x x x ++=．【答案】ACD 【解析】【分析】根据辅助角公式把函数的关系变形为正弦型函数，进一步利用正弦型函数的性质应用即可判断各选项.【详解】由()sin f x x x =，得()π2sin 3f x x æö=+ç÷èø.对于A ，当π0,2x éùÎêëû时，ππ56π,33x éù+Îêúëû，当πππ332x £+£即π06x ££时，函数()f x 单调递增，所以函数()f x 单调递增区间为π0,6éùêúëû，故A 正确；对于B ，当π6x =-时，ππππsin sin f æöæö-=-+==¹ç÷ç÷èøèø22106636，故B 不正确；对于C ，函数()f x 的图象向左平移(0)m m >个单位长度后，得到()πsin g x x m æö=++ç÷èø23所得的图象关于y 轴对称，所以πππ(Z)m k k +=+Î32,解得ππ(Z)m k k =+Î6，当0k =时，m 的最小值是π6，故C 正确；对于D ，如图所示，实数m 使得方程()f x m =在[]02π，上恰好有三个实数解1x ，2x ，3x ，则必有0x =，或2πx =，此时()πsin f x x æö=+=ç÷èø23π3.所以1237π3x x x ++=，故D 正确.故选：ACD.5分，共20分）13. 计算100的结果为______.【答案】1-【解析】【分析】先求出41=-，所以100425´=，代入即可得出答案.)i 1==+，)()221i 12i i 2ù=+==úû，42i 1==-，所以()1004252511´==-=-.故答案为：1-14. 在正四面体A -BCD 中，二面角A -BC -D 的余弦值是_______ .【答案】13【解析】【分析】根据二面角平面角的定义，结合正四面体的性质，找出该角，由余弦定理，可得答案.【详解】如图，取BC 的中点F ，连接AF ，DF ，则AF BC ^，DF BC ^，即AFD Ð为二面角A BC D --的平面角，设正四面体D ABC -的棱长为6，在正ABC V 中，sin 60AF AB==o sin 60DF BD ==o由余弦定理2221cos 23FD FA AD AFD FD FA +-Ð===××.故答案为：13.15. 若向量a r 、b r 满足1a =r ，2b =r ，且a r 与b r 的夹角为3p，则a b -=rr ________．【解析】【分析】利用平面向量数量积的运算律求得2a b -r r的值，进而可求得a b -r r 的值.【详解】由于向量a r 、b r 满足1a =r ，2b =r ，且a r 与b r 的夹角为3p ，则cos 13a b a b p ×=×=r r r r ，()222223a b a ba ab b -=-=-×+=r r r rr r r r Q，因此，a b -=r r .【点睛】本题考查利用平面向量的数量积求向量的模，考查计算能力，属于基础题.16. ABC V 中60B =o，AC =2AB BC +最大值______．【答案】【解析】【分析】根据余弦定理，列出方程，利用一元二次方程根的判别式，可得答案.详解】设AB c =，AC b =，BC a =，由余弦定理：222cos 2a c b B ac+-=，所以2223a c ac b +-==，设2c a m +=，则2c m a =-，代入上式得227530a am m -+-=，方程有解，所以28430m D =-³，故m £，当m =时，此时a =，c =，符合题意，因此最大值为.故答案为：.四、解答题（本大题共6小题，共70分.解答应有文字说明，证明过程或演算步骤）17. 已知三个点A (2，1)，B (3，2)，D (－1，4)．（1）求证：AB uuu r ⊥AD uuu r；（2）要使四边形ABCD 为矩形，求点C 的坐标．【答案】（1）证明见解析（2）(0，5)【解析】【分析】（1）计算AB AD ×uuu r uuu r得其为0可证；（2）由AB uuu r ＝DC uuu r可得C 点坐标．【小问1详解】证明：A (2，1)，B (3，2)，D (－1，4)．∴AB uuu r ＝(1，1)，AD uuu r＝(－3，3)．【又∵AB uuu r ·AD uuu r ＝1×(－3)＋1×3＝0，∴AB uuu r ⊥AD uuu r .【小问2详解】∵AB uuu r ⊥AD uuu r ，若四边形ABCD 为矩形，则AB uuu r ＝DC uuu r.设C 点的坐标为(x ，y )，则有(1，1)＝(x ＋1，y －4)，∴11,41,x y +=ìí-=î∴0,5.x y =ìí=î∴点C 的坐标为(0，5)．18. 在正三棱柱111ABC A B C -中，1AB AA =，D 是1CC 的中点，F 是1A B 的中点.（1）求证：//DF 平面ABC ；（2）求证：AF BD ^ .【答案】（1）证明见解析（2）证明见解析【解析】【分析】（1）取AB 的中点E ，连接CE 、EF ，证明出四边形CDFE 为平行四边形，可得出//DF CE ，再利用线面平行的判定定理可证得结论成立；（2）证明出CE ^平面11AA B B ，可得出CE AF ^，可得出AF DF ^，再证明出1AF A B ^，利用线面垂直的判定定理与性质定理可证得结论成立.【小问1详解】证明：取AB 的中点E ，连接CE 、EF ，如下图所示：在正三棱柱111ABC A B C -中，11//AA CC 且11AA CC =，因为E 、F 分别为AB 、1A B 的中点，则1//EF AA 且112EF AA =，D Q 为1CC 的中点，则1CD AA //且112CD AA =，//CD EF \且CD EF =，所以，四边形CDFE 为平行四边形，故//DF CE ，DF ËQ 平面ABC ，CE Ì平面ABC ，因此，//DF 平面ABC .【小问2详解】证明：1AA ^Q 平面ABC ，CE Ì平面ABC ，1CE AA \^，ABC Q V 为等边三角形，E 为AB 的中点，则CE AB ^，1AB AA A Ç=Q ，AB 、1AA Ì平面11AA B B ，CE \^平面11AA B B ，AF ÌQ 平面11AA B B ，则AF CE ^，//DF CE Q ，AF DF \^，1AB AA =Q ，F 为1A B 的中点，则1AF A B ^，1A B DF F =Q I ，1A B 、DF Ì平面1A BD ，AF \^平面1A BD ，BD ÌQ 平面1A BD ，AF BD \^.19. 当实数m 为何值时，复数()()2281532i 8z m m m m -+-+=+在复平面内的对应点满足下列条件：（1）位于第四象限；（2）位于实轴负半轴上（不含原点）；（3）在上半平面（含实轴）．【答案】（1）73m -<<（2）4m =（3）7m £-或4m ≥【解析】【分析】（1）由实部大于0且虚部小于0列出不等式组求解；（2）由实部小于0且虚部等于0列式求解；（3）由虚部大于或等于0列出不等式求解．【小问1详解】要使点位于第四象限，则有228150,3280,m m m m ì-+>í+-<î∴35,74,m m m <>ìí-<<î或∴73m -<<；【小问2详解】要使点位于实轴负半轴上（不含原点），则有228150,3280,m m m m ì-+<í+-=î∴35,74,m m m <<ìí=-=î或∴4m =；【小问3详解】要使点在上半平面（含实轴），则有20328m m +-³，解得7m £-或4m ≥．20. 已知ABC V 的三边长分别是3AC =，4BC =，5AB =，以AB 所在直线为轴，将此三角形旋转一周，求所得旋转体的表面积和体积．【答案】845p ，485p 【解析】【分析】根据旋转体的定义，明确组合体是由同底的两个圆锥组成的，结合圆锥的侧面积和体积公式可得答案.【详解】如图，在ABC V 中，过C 作CD ⊥AB ，垂足为D .由AC ＝3，BC ＝4，AB ＝5，知AC 2＋BC 2＝AB 2，则AC ⊥BC ，∵BC ·AC ＝AB ·CD ，∴CD ＝125，记为r ＝125，那么ABC V 以AB 所在直线为轴旋转所得旋转体是两个同底的圆锥，且底半径r ＝125，母线长分别是AC ＝3，BC ＝4，所以S 表面积＝πr ·(AC ＋BC )＝π×125×(3＋4)＝845π，V ＝13πr 2(AD ＋BD )＝13πr 2·AB ＝13π×12()52×5＝485π.21. 在锐角三角形ABC V 中，角,,A B C 对边分别为,,a b c2sin 0b A -=．（1）求角B 的大小；（2）若5a c +=，且,a c b >=，求AB AC ×u u u r u u u r的值．的【答案】（1）3B p=；（2）1AB AC ×=uuu r uuu r ．【解析】【分析】（1）利用正弦定理，直接计算求解即可.（2）利用余弦定理，计算求出cos A ，然后，利用向量的内积公式，即可求解.【小问1详解】2sin 0b A -=2sin sin 0A B A -=，因为sin 0A ¹，所以sin B =，又B 为锐角，所以3B p =．【小问2详解】由（1）知，3B p =，因为b =，所以根据余弦定理得2272cos 3a c ac p =+-，整理得2()37a c ac +-=，又5a c +=，所以6ac =，又a c >，所以3,2a c ==，于是222cos 2b c a A bc +-===所以||||cos 21AB AC AB AC A ×===uuu r uuu r uuu r uuu r ．22. 如图，四面体ABCD 中，O 、E 分别是BD 、BC 的中点，2,CA CB CD BD AB AD ======（1）求证：AO ^平面BCD ；（2）求异面直线AB 与CD 所成角的大小；（3）求点E 到平面ACD 的距离.【答案】（1）证明见解析（2）（3【解析】【分析】（1）根据线面垂直判定定理，结合勾股定理和等腰三角形的性质，可得答案；（2）根据异面直线夹角的定义，结合中位线性质和余弦定理，可得答案；（3）根据等体积法，结合三角形面积公式，可得答案.【小问1详解】证明：,,.BO DO AB AD AO BD ==\^Q 则222AO BO AB +=，即1AO =，,,.BO DO BC CD CO BD ==\^Q 则222CO BO BC +=，即CO =，在AOC △中，由已知可得2222,AC AO CO AC =\+=，.AO OC ^BD OC O Ç=Q ，,BD OC Ì平面BCD ，AO \^平面BCD【小问2详解】取AC 的中点M ，连结OM 、ME 、OE ，由E 为BC 的中点知,ME AB OE DC ////\直线OE 与EM 所成的锐角就是异面直线AB 与CD 所成的角在OME V 中，111,22EM AB OE DC ====OM Q 是直角AOC △斜边AC 上的中线，11,2OM AC \==222cos 2OE EM OM OEM OE EM +-\Ð==××\异面直线AB 与CD 所成角的大小为；【小问3详解】设点E 到平面ACD 的距离为.h 11,.33E ACD A CED ACDCED V V h S AO S --=\××=××V V Q 在ACD △中，2,CA CD AD ===12ACD S ==\V 而11,12CED AO S ===V，AC CED D AO S h S ×\===V V \点E 到平面ACD。

2023-2024学年宁夏回族自治区石嘴山市平罗县高一下册3月月考数学试题(含解析)

2023-2024学年宁夏回族自治区石嘴山市平罗县高一下册3月月考数学试题一、单选题1．已知角θ的终边经过点(1,P ，则cos θ的值为（）A．BC ．12-D ．12【正确答案】D【分析】利用三角函数的定义进行求解.【详解】因为角θ的终边经过点(1,P ，所以1cos 2θ==.故选：D.2．已知4cos 5=-α，且sin 0α<，则tan α=（）A ．34B ．34-C ．43D ．43-【正确答案】A【分析】由已知可求出3sin 5α=-，进而即可得出tan α的值.【详解】因为4cos 5=-α，且sin 0α<，所以，3sin 5α===-.所以，sin 3tan cos 4ααα==.故选：A.3．如图，在ABCD Y 中，E 是BC 的中点，若AB a=，AD b =，则DE 等于（）A ．12a b-r r B ．12a b+ C ．12a b+ D ．12a b-r r 【正确答案】D【分析】利用三角形法则与平行四边形法则表示向量.【详解】因为E 是BC 的中点，AB a=，AD b = ，所以111222CE CB AD b ==-=- ，所以12DE DC CE AB CE a b =+=+=- .故选：D.4．已知向量()2,4a =r ，()1,b x = ，若向量a b ⊥，则实数x 的值是（）.A ．2-B ．12-C ．12D ．2【正确答案】B【分析】利用向量垂直的坐标表示即可求解.【详解】,240a b x ⊥∴+= ，解得12x =-.故选：B5．已知ABC 中，1,45a b B ===，则A =（）A ．150B ．150 或30C ．30D ．60【正确答案】C【分析】根据正弦定理以及大边对大角即可解出．【详解】因为sin sin a b A B =，所以1sin A =解得1sin 2A =，而a b <，所以090A << ，所以A =30 ．故选：C ．6．在ABC 中，若sin sin b A a C =，则ABC 的形状是（）A ．等边三角形B ．直角三角形C ．等腰三角形D ．等腰直角三角形【正确答案】C【分析】根据正弦定理进行判断即可.【详解】根据正弦定理由sin sin b A a C ba ac b c =⇒=⇒=，所以该三角形是等腰三角形，故选：C7．函数()cos 2f x x π⎛⎫=- ⎪⎝⎭是（）A ．奇函数，在区间0,2π⎛⎫⎪⎝⎭上单调递增B ．奇函数，在区间0,2π⎛⎫⎪⎝⎭上单调递减C ．偶函数，在区间0,2π⎛⎫⎪⎝⎭上单调递增D ．偶函数，在区间0,2π⎛⎫⎪⎝⎭上单调递减【正确答案】A【分析】先利用诱导公式化简函数，再利用正弦函数性质直接判断奇偶性和单调性即可.【详解】因为函数()cos sin 2f x x x π⎛⎫=-= ⎪⎝⎭，是正弦函数，所以()f x 是奇函数，且在区间0,2π⎛⎫⎪⎝⎭上单调递增.故选：A.8．ABC 的三内角A B C ，，所对边分别为a b c ，，，若222a b c ab +-=，则角C 的大小（）．A ．π6B ．π3C ．π2D ．2π3【正确答案】B【分析】根据余弦定理直接求解即可.【详解】解：由余弦定理得2221cos 222a b c ab C ab ab +-===，因为()cos 0,πC ∈，所以π3C =.故选：B二、多选题9．下列给出的各角中，与2π3-终边相同的角有（）A ．4π3B ．8π3-C ．7π3D ．16π3【正确答案】ABD【分析】根据终边相同的角的定义逐一验证即可判断出选项.【详解】由题意可知，与2π3-终边相同的角的集合为2π2π,Z 3k k αα⎧⎫=-+∈⎨⎬⎩⎭|，由此可得，1k =时，4π3α=，即A 正确；1k =-时，8π3α=-，即B 正确；7π3α=时，32k =∉Z ，所以C 错误；3k =时，16π3α=，即D 正确；故选：ABD10．化简以下各式，结果为0的有（）A ．AB BC CA++ B ．AB AC BD CD-+- C ．OA OD AD-+ D ．NQ QP NM MP++- 【正确答案】ABC【分析】根据平面向量的加减法运算逐个判断可得答案.【详解】对于A ，AB BC CA ++ 0AC AC =-=，故A 正确；对于B ，AB AC BD CD -+- ()()AB BD AC CD =+-+ 0AD AD =-= ，故B 正确；对于C ，OA OD AD-+ ()OA AD OD =+- 0OD OD =-= ，故C 正确；对于D ，NQ QP NM MP ++- NP PM NM =++ NM NM =+ 2NM =，故D 不正确.故选：ABC.11．下列说法中正确的是（）A ．若12,e e 为单位向量，则12e e =B ．若a 与b共线，则a b = 或a b=-r r C ．若0a =，则0a = D ．a a是与非零向量a共线的单位向量【正确答案】CD【分析】根据向量的基本概念，以及零向量和单位向量的定义，逐项判定，即可求解.【详解】对于A 中，向量12,e e的方向不一定相同，所以A 错误；对于B 中，向量a 与b的长度不一定相等，所以B 错误；对于C 中，由0a =，根据零向量的定义，可得0a = ，所以C 正确；对于D 中，由1a a a a =⋅，可得a a 与向量a同向，又由aa的模等于1，所以a a是与非零向量a共线的单位向量，所以D 正确.故选：CD.12．要得到函数πsin 23y x ⎛⎫=+ ⎪⎝⎭的图象，只要将函数sin y x =图象上所有的点（）A ．横坐标缩短到原来的12（纵坐标不变），再将所得图象向左平移π3个单位B ．横坐标缩短到原来的12（纵坐标不变），再将所得图象向左平移π6个单位C ．向左平移π3个单位，再将所得图象每一点的横坐标缩短到原来的12（纵坐标不变）D ．向左平移π6个单位，再将所得图象每一点的横坐标缩短到原来的12（纵坐标不变）【正确答案】BC【分析】根据周期变换和平移变换的原则即可得解.【详解】要得到函数πsin 23y x ⎛⎫=+ ⎪⎝⎭的图象，只要将函数sin y x =图象上所有的点横坐标缩短到原来的12（纵坐标不变），再将所得图象向左平移π6个单位；或者向左平移π3个单位，再将所得图象每一点的横坐标缩短到原来的12（纵坐标不变）.故选：BC.三、填空题13．已知扇形的圆心角为2rad ，扇形的半径长为10cm ，则扇形的面积为______2cm .【正确答案】100【分析】先利用弧长公式计算出弧长，再利用扇形面积12S lr =求解即可【详解】因为扇形的圆心角为2rad ，扇形的半径长为10cm ，所以扇形弧长为21020cm l =´=，则扇形的面积212010100cm 2S =⨯⨯=.故10014．已知平面向量()1,2a =- ，(),3b m =- ，若2a b + 与a共线，则m =______.【正确答案】32##1.5【分析】确定()212,4a b m +=-+-，根据平行得到()4312m m -=--+，解得答案.【详解】()1,2a =- ，(),3b m =- ，则()212,4a b m +=-+- ，()2a b a + ∥，故()4212m =-+，解得32m =故3215．已知||1,||a b =a与b 的夹角为4π，则a 在b 方向上的投影向量为__.【正确答案】12br【分析】由向量投影的定义即可求得则a 在b方向上的投影向量.【详解】a在b 方向上的投影向量为1||cos 42||b a b b π⋅=.故12b 16．如图，中华中学某班级课外学习兴趣小组为了测量某座山峰的高气度，先在山脚A 处测得山顶C 处的仰角为60°，又利用无人机在离地面高400m 的M 处（即400MD =），观测到山顶C 处的仰角为15°，山脚A 处的俯角为45°，则山高BC =___________m.【正确答案】600【分析】确定AM =45ACM ∠=︒，75MAC ∠=︒，在MAC △中，利用正弦定理计算得到答案.【详解】45AMD ∠=︒，则AM ==，451560CMA ∠=︒+︒=︒,60CAB ∠=︒，故18060MAC ∠=︒-︒4575-︒=︒，180756045ACM ∠=︒-︒-︒=︒，在MAC △中，由正弦定理得sin sin AC MA AMC ACM =∠∠，即sin60sin45AC =︒︒，解得AC =sin60600BC AC =︒=.故600四、解答题17．已知4sin5θ=，θ为第二象限角．(1)求sin2θ的值；(2)求πcos6θ⎛⎫-⎪⎝⎭的值．【正确答案】(1)24 25 -【分析】（1）根据同角三角函数结合已知得出cosθ，即可根据二倍角的正弦公式代入数值得出答案；（2）根据两角和差的余弦公式代入数值得出答案.【详解】（1）4 sin5θ=，θ为第二象限角，3cos5θ∴===-，则4324sin22sin cos25525θθθ⎛⎫==⨯⨯-=-⎪⎝⎭；（2）πππ341cos cos cos sin sin666552θθθ⎛⎫-=+=-+⨯⎪⎝⎭18．已知函数()()2cos2cos1f x x x x x=+-∈R.(1)求函数()f x的最小正周期和对称轴的方程.(2)当π0,2x⎡⎤∈⎢⎥⎣⎦时，求函数()f x的值域.【正确答案】(1)π,ππ,Z62kx k=+∈(2)[]1,2-【分析】（1）利用三角恒等变换可得函数解析式，再根据三角函数的性质求解；（2）根据三角函数的性质即可求给定区间的值域.【详解】（1）()2πcos2cos1sin2cos22sin(2)6f x x x x x x x=+-+=+，所以最小正周期为2ππ2T==,令ππ2π,Z 62x k k +=+∈解得ππ,Z 62k x k =+∈，所以对称轴方程为ππ,Z 62k x k =+∈.（2）因为π0,2x ⎡⎤∈⎢⎥⎣⎦，所以ππ7π2,666x ⎡⎤+∈⎢⎣⎦，所以()[]π2sin(2)1,26f x x =+∈-,即()f x 的值域为[]1,2-.19．已知||3a = ，||4b = ，a 与b的夹角为60°．试求：（1）||a b + ；（2）a b + 与a b -的夹角θ的余弦值．【正确答案】（1）a b += （2）（1）由向量的模的运算及数量积运算即可得解；（2）由()()cos ||||a b a b a b a b θ+⋅-=+- ，结合向量的数量积求解即可.【详解】解：（1）∵222||2916234cos 6037a b a b a b ︒+=++⋅=++⨯⨯⨯= ，∴||a b +=（2）∵222||2916234cos 6013a b a b a b ︒-=+-⋅=+-⨯⨯⨯=，∴||a b -=．∴()()cos ||||a b a b a b a b θ+⋅-===+- 本题考查了向量模的运算，重点考查了向量的数量积运算及向量夹角的运算，属基础题.20．在ABC 中，角,,A B C 的对边分别为,,a b c ，若cos cos 2cos a B b A c C +=.(1)求角C 的大小；(2)若ABC的面积为c =，求ABC 的周长.【正确答案】(1)π3C =(2)6+【分析】（1）利用正弦定理边化角，结合两角和差正弦公式可化简求得cos C ，由此可得C ；（2）由三角形面积公式可求得ab ，利用余弦定理可构造方程求得a b +，由此可得三角形周长.【详解】（1）由正弦定理得：sin cos sin cos 2sin cos A B B A C C +=，()()sin sin πsin 2sin cos A B C C C C ∴+=-==，()0,πC ∈ ，sin 0C ∴≠，1cos 2C ∴=，则π3C =.（2）1sin 24ABC S ab C ab === 8ab ∴=，由余弦定理得：()()222222cos 32412c a b ab C a b ab a b =+-=+-=+-=，解得：6a b +=，ABC ∴ 的周长6L a b c =++=+21．在ABC 中，6CA =，8AB =，π2BAC ∠=，D 为边BC 中点．(1)求AD CB ⋅的值；(2)若点P 满足()CP CA λλ=∈R ，求PB PC ⋅的最小值；【正确答案】(1)14(2)最小值为9-【分析】（1）以A 为坐标原点，边AC AB 、所在的直线为x y 、轴的正方向建立平面直角坐标系求出AD 、CB的坐标，再由向量数量积的坐标运算可得答案；（2）根据点P 在AC 上，设(),0P x ，求出PB 、PC的坐标，则()(),86,0⋅=-⋅- PB PC x x ，利用二次函数配方求最值可得答案.【详解】（1）如图，以A 为坐标原点，边AC AB 、所在的直线为x y 、轴的正方向建立平面直角坐标系，所以()0,0A ，()0,8B ，()6,0C ，D 为边BC 中点，所以()3,4D ，()3,4= AD ，()6,8=-CB ，则183214⋅=-+=AD CB ；（2）若点P 满足()CP CA λλ=∈R，则点P 在AC 上，由（1），设(),0P x ，则(),8=- PB x ，()6,0=-PC x ，则()()()2,86,039⋅=-⋅-=-- PB PC x x x ，所以当3x =时PB PC ⋅的最小值为9-.22．在平面四边形ABCD 中，3ABC π∠=，2ADC π∠=，4BC =.（1）若△ABC 的面积为33AC ；（2）若33AD =3ACB ACD π∠=∠+，求tan ACD ∠.【正确答案】（113（2337【分析】（1）应用三角形面积公式有1sin 2ABC S AB BC ABC =⋅⋅∠△，可求AB ，由余弦定理即可求AC ；（2）设ACD α∠=，在Rt ACD 中sin ADAC α=，在△ABC 中应用正弦定理有sin sin BC ACBAC ABC=∠∠，即可求tan α，得解.【详解】（1）在△ABC 中，4BC =，3ABC π∠=，∴1sin 332ABC S AB BC ABC =⋅⋅∠= 3AB =，在△ABC 中，由余弦定理得2222cos 13AC AB BC AB BC ABC =+-⋅⋅∠=，AC ∴=（2）设ACD α∠=，则33ACB ACD ππα∠=∠+=+，在Rt ACD 中，AD =，易知：sin AD AC α=在△ABC 中，3BAC ACB ABC ππα∠=-∠-∠=-，由正弦定理得sin sin BC AC BAC ABC =∠∠，即4sin 3πα=⎛⎫- ⎪⎝⎭，32sin 3sin()sin 32παααα∴=-=-，可得tan α=tan ACD ∠=.。

宁夏石嘴山市高三数学第二次联考试题理新人教A版

高三第二次联考数学试题（理科）全解全析一、选择题1．设集合(){|ln 1,}A x y x y R ==-∈，集合2{|,}B y y x x R ==∈，则A B = （） A. φB. [0，1)C. (1，+∞)D.（－∞，1）【解析】因为{|10}{|1}A x x x x =->=<，{|0}B y y =≥，所以[0,1)A B = ，故选择B 。

2．若复数12ω=（i 为虚数单位），则1ω-等于（）A. 2ωB. 2ω-C.ω-D.1ω-【解析】因为111122ω-=+-=-，2211()22ω==-+，所以21ωω-=，故选择A 。

3．公差不为零的等差数列{}n a 中，236,,a a a 成等比数列，则其公比为（）A ．1B ．2C ．3D ．4【解析】设等差数列{}n a 的公差为d ，则21a a d =+，312a a d =+，615a a d =+。

因为236,,a a a 成等比数列，所以2111()(5)(2)a d a d a d ++=+，化简得212d a d =-。

因为0d ≠，所以12d a =-，21a a =-，313a a =-，公比312133a a q a a -===-，故选择C 。

4．已知命题p ：m 、n 为直线，α为平面，若m ∥n ，α⊂n ，则m ∥α；命题q ：若a ＞b ，则ac ＞bc ，则下列命题为真命题的是（） A. p 或qB. ⌝p 或qC. ⌝p 且qD. p 且q【解析】若m ∥n ，α⊂n ，则m ∥α，也可能m α⊂，所以命题p 是假命题；若a ＞b ，当0c =时，ac bc =；当0c <时，ac bc <，所以命题q 也是假命题，综上所述，p 或q 为假命题；⌝p 或q 为真命题；⌝p 且q 为假命题；p 且q 为假命题，故选择B 。

5．设22 1(32)n x dx =-⎰，则n xx )2(-展开式中含2x 项的系数是（）A ．-80B ．80C ．-40D ．40【解析】321(2)|5n x x =-=，通项公式354542155((1)2r r r r rr T C xC x --+==-，令3522r -=，2r =，所以5(x 展开式中含2x 项的系数是2425(1)240C -=，故选择D 。

宁夏石嘴山市第一中学2025届高三第二次联考数学试卷含解析

宁夏石嘴山市第一中学2025届高三第二次联考数学试卷注意事项：1．答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

2．选择题必须使用2B 铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

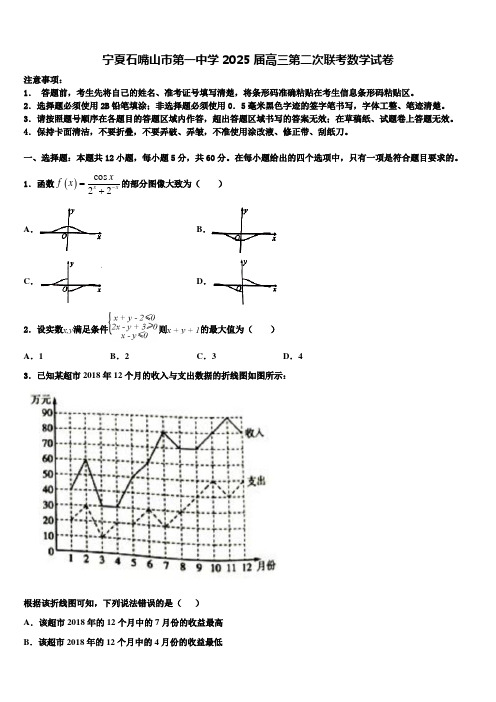
1．函数()cos 22x xxf x -=+的部分图像大致为（）A ．B ．C ．D ．2．设实数满足条件则的最大值为（） A ．1B ．2C ．3D ．43．已知某超市2018年12个月的收入与支出数据的折线图如图所示：根据该折线图可知，下列说法错误的是（） A ．该超市2018年的12个月中的7月份的收益最高 B ．该超市2018年的12个月中的4月份的收益最低C ．该超市2018年1-6月份的总收益低于2018年7-12月份的总收益D ．该超市2018年7-12月份的总收益比2018年1-6月份的总收益增长了90万元4．定义在R 上的函数()()f x x g x =+，()22(2)g x x g x =--+--，若()f x 在区间[)1,-+∞上为增函数，且存在20t -<<，使得(0)()0f f t ⋅<.则下列不等式不一定成立的是（）A ．()2112f t t f ⎛⎫++>⎪⎝⎭B ．(2)0()f f t ->>C ．(2)(1)f t f t +>+D ．(1)()f t f t +>5．函数2|sin |2()61x x f x x=-+的图象大致为（）A ．B ．C ．D ．6．已知R 为实数集，{}2|10A x x =-≤，1|1B x x ⎧⎫=≥⎨⎬⎩⎭，则()A B =R（）A ．{|10}x x -<≤B ．{|01}x x <≤C ．{|10}x x -≤≤D ．{|101}x x x -≤≤=或7．执行程序框图，则输出的数值为（）A ．12B ．29C ．70D ．1698．已知点P 在椭圆τ：2222x y a b+=1(a>b >0)上，点P 在第一象限，点P 关于原点O 的对称点为A ，点P 关于x 轴的对称点为Q ，设34PD PQ =，直线AD 与椭圆τ的另一个交点为B ，若PA ⊥PB ，则椭圆τ的离心率e =（） A ．12B ．22C ．32D ．339．如图，在平行四边形ABCD 中，O 为对角线的交点，点P 为平行四边形外一点，且AP OB ，BP OA ，则DP =（）A ．2DA DC +B ．32DA DC + C ．2DA DC +D ．3122DA DC +10．设命题p:n ∃>1,n 2>2n ,则⌝p 为（） A ．21,2n n n ∀>> B ．21,2n n n ∃≤≤ C ．21,2n n n ∀>≤D ．21,2n n n ∃>≤11．若平面向量,,a b c ，满足||2,||4,4,||3a b a b c a b ==⋅=-+=，则||c b -的最大值为（）A ．523B ．523C ．2133D ．213312．已知ABC 的内角A 、B 、C 的对边分别为a 、b 、c ，且60A =︒，3b =，AD 为BC 边上的中线，若72AD =，则ABC 的面积为（） A 253B 153C ．154D 353二、填空题：本题共4小题，每小题5分，共20分。

宁夏高一下学期数学第二次月考试卷

宁夏高一下学期数学第二次月考试卷姓名:________班级:________成绩:________一、选择题（本大题共 12 小题，每小题 5 分，） (共 12 题；共 60 分)1. （5 分）下列说法错误的是（）A . 多面体至少有四个面B . 九棱柱有 9 条侧棱，9 个侧面，侧面为平行四边形C . 长方体、正方体都是棱柱D . 三棱柱的侧面为三角形2. （5 分）若一个等腰三角形采用斜二测画法作出其直观图，其直观图面积是原三角形面积的（）A. 倍 B . 2倍C.倍D. 倍3. （5 分） (2017·合肥模拟) 已知一个圆锥底面半径为 1，母线长为 3，则该圆锥内切球的表面积为（） A.πB. C . 2π D . 3π 4. （5 分）一个几何体的三视图如图所示，则该几何体的体积为（）第 1 页共 12 页A.1 B.2 C.3 D.4 5. （5 分） (2019 高二下·静安期末) 半径为 2 的球的表面积为（） A. B. C. D. 6. （5 分） (2017 高二上·武清期中) 用“斜二测”画法画出△ABC（A 为坐标原点，AB 在 x 轴上）的直观图为△A′B′C′，则△A′B′C′的面积与△ABC 的面积的比为（）A.B.C.D. 7. （5 分）已知球的直径 SC=2，A，B 是该球球面上的两点，AB=1，∠ASC=∠BSC=30°，则棱锥 S﹣ABC 的体积为（）A.第 2 页共 12 页B.C.D.8. （5 分） (2012·湖南理) 已知两条直线 l1：y=m 和 l2：y=（m＞0），l1 与函数 y=|log2x|的图象从左至右相交于点 A，B，l2 与函数 y=|log2x|的图象从左至右相交于点 C，D．记线段 AC 和 BD 在 X 轴上的投影长度分别为 a，b，当 m 变化时，的最小值为（）A . 16B.8C.8D.49. （5 分）在△ABC 中，a、b、c 分别是角 A、B、C 的对边，若角 A、B、C 依次成等差数列，且﹣x2+5x﹣4 ＞0 的解集为{x|a＜x＜c}，则 S△ABC=（）A.B.2C.3D.410. （5 分） (2016 高三上·黄冈期中) 在等差数列{an}中，已知 a4+a8=16，则该数列前 11 项和 S11=（）A . 58B . 88C . 143第 3 页共 12 页D . 176 11. （5 分） (2018·海南模拟) 我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：“一座 7 层塔共挂了 381 盏灯，且相邻两层中的下一层灯数是上一层灯数的 2 倍，则塔的顶层共有灯多少？”现有类似问题：一座 5 层塔共挂了 242 盏灯，且相邻两层中的下一层灯数是上一层灯数的 3 倍，则塔的底层共有灯（） A . 162 盏 B . 114 盏 C . 112 盏 D . 81 盏12. （5 分） (2018·株洲模拟) 已知各项为正数的等比数列满足，，则（）A . 64B . 32C . 16D.4二、填空题（本大题共 4 小题，每小题 5 分。

宁夏石嘴山市高一数学下学期第二次(5月)月考试题(扫描

宁夏石嘴山市2016-2017学年高一数学下学期第二次（5月）月考试题I 卷一、选择题（每小题5分，共60分）.1、已知向量(1,3)a =r ,()1,2b =-r，则a r 与b r 的夹角θ等于（）A.3π B. 4π C. 6π D. 4π-2、设tan ,tan αβ是方程2320x x -+=的两根，则tan()αβ+的值( ) A. -3 B.-1 C. 1 D. 33、设向量()1,2a =r ，(2,3)b =r , 若向量a b λ-r r与向量(5,6)c =--r 共线，则λ的值为( )A.43 B. 413 C. 49- D. 4 4、平面四边形ABCD 中, ()0,0AB CD AB AD AC +=-•=u u u r u u u r r u u u r u u u r u u u r，则四边形ABCD 是（）A ．矩形B ．菱形C ．正方形D ．梯形 5、已知α满足1sin 3α=，则cos cos 44ππαα⎛⎫⎛⎫+-= ⎪ ⎪⎝⎭⎝⎭（） A. 2518-B. 2518C. 718- D. 7186、已知ABC ∆的边BC 上有一点D 满足3BD DC =u u u r u u u r ，则AD u u u r可表示为（）A. 23AD AB AC =-+u u u r u u u r u u u rB. 3144AD AB AC =+u u u r u u u r u u u rC. 1344AD AB AC =+u u u r u u u r u u u rD. 2133AD AB AC=+u u u r u u u r u u u r7.已知13sin cos ,cos sin ,2αβαβ-=+=则sin()αβ-=（） A. -1 B.12 C. 1 D. 12-8、已知(1,2),(3,4),(2,2),(3,5)A B C D --，则向量AB u u u r在向量CD uuu r 方向上的投影为（）A.105 B. 105 C .3105 D. 1059、已知(3,0),(0,3),(cos ,sin )A B C αα，若1AC BC •=-u u u r u u u r ，则sin 4πα⎛⎫+= ⎪⎝⎭（）A.13 B. 33 C. 23D. 2310、下列语句：（1）若0a b →→•=，则a b →→⊥。

宁夏石嘴山市第三中学高一数学上学期第二次考试试题

石嘴山三中高一年级(上)第二次月考数学试卷一、选择题：本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集U ={1，2，3，4，5，6}，集合P ={1，3，5}，Q ={1，2，4}，则U P Q （）ð=（） A.{1}B.{3，5}C.{1，2，4，6}D.{1，2，3，4，5}1已知A (-1,2),B (-2,4),则直线AB 的斜率为( )A .-2B .-21 C. 21D.23.如图,一个简单组合体的正视图和侧视图相同,是由一个正方形与一个正三角形构成,俯视图中,圆的半径为3错误！未找到引用源。

.则该组合体的表面积为( ).A.15πB.18πC.21πD.24π4. 函数()2log (1)f x x =+的定义域为（）A ．[)1,3-B ．()1,3-C ．[]1,3-D ．(1,3]- 5. 下列函数中，既是偶函数又在(0，＋∞)上单调递增的函数是( )A. y ＝x 3B. y ＝|x |＋1C. y ＝－x 2＋1 D. y ＝2－|x |6. 若a ＝20.5，b ＝log π3，c ＝log 222，则有( ) A. a >b >c B. b >a >c C. c >a >b D. b >c >a7.已知两个不同的平面α、β和两条不重合的直线，m 、n ，有下列四个命题： ①若m ∥n ，m ⊥α，则n ⊥α ②若m ⊥α，m ⊥β，则α∥β； ③若m ⊥α，m ∥n ，n ⊂β，则α⊥β； ④若m ∥α，α∩β=n ，则m ∥n ，其中不正确的命题的个数是（）A ．0个B ．1个C ．2个D ．3个8．函数f （x ）=2x+x ﹣2的零点所在的一个区间是（）A ．（﹣2，﹣1）B ．（﹣1，0）C ．（0，1）D ．（1，2） 9．某三棱锥的三视图如图所示，该三棱锥的表面积是（）A ．28＋65B ．30＋65C ．56＋125D ．60＋12510.在如图所示的锐角三角形空地（底边长为40m ，高为40m ）中，欲建一个面积不小于2300m 的内接矩形花园（阴影部分），则其边长x （单位：m ）的取值范围是（）A ．[]15,20B ．[]12,25C ．[]10,30D ．[]20,3011.在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球，若AB BC ⊥，6AB =，8BC =，13AA =，则V 的最大值是（）（A ）4π （B ）92π （C ）6π （D ）323π12．如图，矩形ABCD 中，2AB AD =，E 为边AB 的中点，将ADE ∆沿直线DE 翻折成1A DE ∆，若M 为线段1A C 的中点，则在ADE ∆翻折过程中，下面四个命题中不正确的是（）A ．||BM 是定值B ．点M 在某个球面上运动C ．存在某个位置，使1DE AC ⊥D ．存在某位置，使//MB 平面1A DE 二、填空题：本大题共4小题,每小题5分13. 如图,∆A'O'B'是∆AOB 用斜二测画法画出的直观图,则∆AOB 的面积是 .14. 设三棱锥P －ABC 的顶点P 在平面ABC 上的射影是H ，给出下列命题：①若PA ⊥BC ，PB ⊥AC ，则H 是△ABC 的垂心；②若PA 、PB 、PC 两两互相垂直，则H 是△ABC 的垂心； ③若∠ABC ＝90°，H 是AC 的中点，则PA ＝PB ＝PC ； ④若PA ＝PB ＝PC ，则H 是△ABC 的外心．请把正确命题的序号填在横线上________．15.如图，正三棱柱的底面边长为1，体积为3，则异面直线A A 1与C B 1所成的角正切值为16. 若函数f (x )=(x+a )(bx+2a )(常数a ,b ∈R )是偶函数,且它的值域为(-∞,4],则该函数的解析式f (x )= .三.解答题：解答应写出文字说明,证明过程或演算步骤.17(10分)．求值：（1 （2）已知lg 2,lg3a b ==，求9lg5．（用,a b 表示） 18. (12分)在正方体1111ABCD A B C D -中，E 、F 分别是AB 、11B C 的中点。

宁夏石嘴山市高一数学下学期第二次(5月)月考试题(扫描版)

宁夏石嘴山市2016-2017学年高一数学下学期第二次（5月）月考试题I 卷一、选择题（每小题5分，共60分）.1、已知向量(1,3)a =r ,()1,2b =-r，则a r 与b r 的夹角θ等于（）A.3π B. 4π C. 6π D. 4π-2、设tan ,tan αβ是方程2320x x -+=的两根，则tan()αβ+的值( ) A. -3 B.-1 C. 1 D. 33、设向量()1,2a =r ，(2,3)b =r , 若向量a b λ-r r与向量(5,6)c =--r 共线，则λ的值为( )A.43 B. 413 C. 49- D. 4 4、平面四边形ABCD 中, ()0,0AB CD AB AD AC +=-•=u u u r u u u r r u u u r u u u r u u u r，则四边形ABCD 是（）A ．矩形B ．菱形C ．正方形D ．梯形 5、已知α满足1sin 3α=，则cos cos 44ππαα⎛⎫⎛⎫+-= ⎪ ⎪⎝⎭⎝⎭（） A. 2518-B. 2518C. 718- D. 7186、已知ABC ∆的边BC 上有一点D 满足3BD DC =u u u r u u u r ，则AD u u u r可表示为（）A. 23AD AB AC =-+u u u r u u u r u u u rB. 3144AD AB AC =+u u u r u u u r u u u rC. 1344AD AB AC =+u u u r u u u r u u u rD. 2133AD AB AC=+u u u r u u u r u u u r7.已知13sin cos ,cos sin ,2αβαβ-=+=则sin()αβ-=（） A. -1 B.12 C. 1 D. 12-8、已知(1,2),(3,4),(2,2),(3,5)A B C D --，则向量AB u u u r在向量CD uuu r 方向上的投影为（）A.105 B. 105 C .3105 D. 1059、已知(3,0),(0,3),(cos ,sin )A B C αα，若1AC BC •=-u u u r u u u r ，则sin 4πα⎛⎫+= ⎪⎝⎭（）A.13 B. 33 C. 23D. 2310、下列语句：（1）若0a b →→•=，则a b →→⊥。

宁夏高一数学下学期第二次月考试卷(含解析)

2016-2017学年宁夏高一（下）第二次月考数学试卷一、选择题（本题共12小题，每小题4分）1．已知角α的终边经过点P（4，﹣3），那么cosα﹣sinα的值是（）A．B．﹣ C．D．2．已知，则的坐标是（）A．（6，﹣5）B．（6，7）C．（6，1）D．（6，﹣1）3．已知，则cos（π+α）的值是（）A．B．﹣ C．D．﹣4．下列各组平面向量中，可以作为基底的是（）A． 1=（0，0），2=（1，﹣2）B． 1=（﹣1，2），2=（5，7）C． 1=（3，5），2=（6，10）D． 1=（2，﹣3），2=（，﹣）5．如图，在平行四边形ABCD中，下列结论中错误的是（）A． =B． +=C． +=D． +=6．在△ABC中，BC=5，AC=8，C=60°，则=（）A．20 B．﹣20 C．D．7．要得到y=3sin2x的图象，只需将y=3sin（2x+）的图象（）A．向右平移个单位B．向左平移个单位C．向左平移个单位D．向右平移个单位8．如图，D，E，F分别是△ABC的边AB，BC，CA的中点，则（）A．B．C．D．9．下列命题中：①若与互为相反向量，则；②若，则；③若，则或；④若，且，则．其中假命题的个数为（）A．1 B．2 C．3 D．410．已知向量与的夹角为120°，，则等于（）A．5 B．4 C．3 D．111．已知函数，x∈R，以下结论：①f（x）的最小正周期是π；②f（x）的图象关于点对称；③f（x）的图象关于直线对称；④f（x）在区间上是增函数；其中正确命题的个数是（）A．4 B．3 C．2 D．112．已知函数y=Asin（ωx+ϕ）（A＞0，ω＞0，|φ|＜），在同一周期内，时取得最大值，时取得最小值﹣，则该函数解析式为（）A． B．C．D．二、填空题（每小题4分，共16分）13．求值：sin750°+cos（﹣660°）+tan（﹣135°）．14．函数的定义域是．15．已知，，且∥，则的坐标为．16．已知，，且，则在方向上的投影为．三、解答题（本题共6道大题，共56分）17．已知=（1，2），=（﹣3，2），当k= 时，（1）k+与﹣3垂直；当k= 时，（2）k+与﹣3平行．18．已知，是同一平面内两个不共线的向量，（1）如果=+， =2﹣， =4+，求证A、B、D三点共线；（2）试确定实数k的值，使和共线．19．已知，是同一平面内两个单位向量，其夹角为60°，如果=2+， =﹣3+2．（1）求（2）求与的夹角．20．已知，（1）求tanα；（2）求sin2α+sinαcosα的值．21．在△ABC中，M是线段AB的中点，，BN与CM相交于点E，设，，（1）用基底，表示和；（2）用基底，表示．22．已知函数（1）求f（x）的单调递增区间；（2）若x∈[0，2π]，求f（x）的值域．2016-2017学年宁夏育才中学孔德校区高一（下）第二次月考数学试卷参考答案与试题解析一、选择题（本题共12小题，每小题4分）1．已知角α的终边经过点P（4，﹣3），那么cosα﹣sinα的值是（）A．B．﹣ C．D．【考点】G9：任意角的三角函数的定义．【分析】由条件利用任意角的三角函数的定义，求得sinα和cosα的值，可得cosα﹣sinα的值．【解答】解：由于角α的终边经过点P（4，﹣3），则x=4、y=﹣3、r=|OP|=5，∴sinα==﹣，cosα==，∴cosα﹣sinα=，故选：D．2．已知，则的坐标是（）A．（6，﹣5）B．（6，7）C．（6，1）D．（6，﹣1）【考点】9J：平面向量的坐标运算．【分析】利用向量坐标运算性质即可得出．【解答】解： =（6，4）﹣（0，﹣3）=（6，7），故选：B．3．已知，则cos（π+α）的值是（）A．B．﹣ C．D．﹣【考点】GO：运用诱导公式化简求值．【分析】由条件利用诱导公式进行化简所给的式子，可得结果．【解答】解：∵已知=﹣cosα，则cos（π+α）=﹣cosα=，故选：A．4．下列各组平面向量中，可以作为基底的是（）A． 1=（0，0），2=（1，﹣2）B． 1=（﹣1，2），2=（5，7）C． 1=（3，5），2=（6，10）D． 1=（2，﹣3），2=（，﹣）【考点】9H：平面向量的基本定理及其意义．【分析】不共线的两个向量才可作为基底，从而判断每个选项的两个向量是否共线，这样即可找出能作为基底的一组向量．【解答】解：A.，∴共线，不能作为基底；B．﹣1×7﹣2×5≠0；∴不共线，可以作为基底；C.；∴共线，不能作为基底；D.；∴共线，不能作为基底．故选B．5．如图，在平行四边形ABCD中，下列结论中错误的是（）A． =B． +=C． +=D． +=【考点】9B：向量加减混合运算及其几何意义．【分析】根据向量加法的平行四边形法则以及平行四边形的性质解答即可．【解答】解：由平行四边形的性质，可得，选项A正确；由向量加法的平行四边形法则，可得，选项B正确；∵，∴选项D正确；∵，∴选项C错误．故选：C．6．在△ABC中，BC=5，AC=8，C=60°，则=（）A．20 B．﹣20 C．D．【考点】9R：平面向量数量积的运算．【分析】利用已知条件，通过向量的数量积求解即可．【解答】解：在△ABC中，BC=5，AC=8，C=60°，则==5×=﹣20．故选：B．7．要得到y=3sin2x的图象，只需将y=3sin（2x+）的图象（）A．向右平移个单位B．向左平移个单位C．向左平移个单位D．向右平移个单位【考点】HJ：函数y=Asin（ωx+φ）的图象变换．【分析】根据两个函数之间的关系即可得到结论．【解答】解：∵y=3sin（2x+）=3sin2（x+），∴y=3sin（2x+）的向右平移个单位，即可得到y=3sin2x的图象，故选：A8．如图，D，E，F分别是△ABC的边AB，BC，CA的中点，则（）A．B．C．D．【考点】9B：向量加减混合运算及其几何意义．【分析】根据向量的四则运算进行求解即可．【解答】解：∵D，E，F分别是△ABC的边AB，BC，CA的中点，∴=， =， =，则++=++=（++）=，故选：A9．下列命题中：①若与互为相反向量，则；②若，则；③若，则或；④若，且，则．其中假命题的个数为（）A．1 B．2 C．3 D．4【考点】2K：命题的真假判断与应用．【分析】由相反向量的定义，模相等方向相反的向量称为相反向量，即可判断①；由单位向量的定义，即可判断②；由向量垂直的条件：数量积为0，即可判断③；由条件可得（﹣）•=0，则或（﹣）⊥，即可判断④．【解答】解：①由相反向量的定义，可得：若与互为相反向量，则，故①正确；②若，即为单位向量，故②错误；③若，则||•||cos＜，＞=0，可得或或⊥，故③错误；④若，且，则（﹣）•=0，则或（﹣）⊥，故④错误．故选：C．10．已知向量与的夹角为120°，，则等于（）A．5 B．4 C．3 D．1【考点】9S：数量积表示两个向量的夹角；93：向量的模．【分析】本题是对向量数量积的考查，根据两个向量的夹角和模之间的关系，用数量积列出等式，再根据和的模两边平方，联立解题，注意要求的结果非负，舍去不合题意的即可．【解答】解：∵向量与的夹角为120°，，∴，∵，∴，∴=﹣1（舍去）或=4，故选B．11．已知函数，x∈R，以下结论：①f（x）的最小正周期是π；②f（x）的图象关于点对称；③f（x）的图象关于直线对称；④f（x）在区间上是增函数；其中正确命题的个数是（）A．4 B．3 C．2 D．1【考点】2K：命题的真假判断与应用．【分析】运用正弦型函数的周期公式，即可判断①；由正弦函数的对称中心的特点，计算即可判断②；由正弦函数的对称轴的特点，计算即可判断③；由正弦函数的增区间，解不等式即可判断④．【解答】解：函数，①f（x）的最小正周期是T==π，故①对；②由f（﹣）=2sin（﹣+）=0，可得f（x）的图象关于点对称，故②对；③由f（）=2sin（+）=，不为最值，f（x）的图象不关于直线对称，故③错；④由2kπ﹣≤2x+≤2kπ+，k∈Z，可得kπ﹣≤x≤kπ+，k∈Z，则f（x）在区间（0，）递增，在（，）递减，故④错．故选：C．12．已知函数y=Asin（ωx+ϕ）（A＞0，ω＞0，|φ|＜），在同一周期内，时取得最大值，时取得最小值﹣，则该函数解析式为（）A． B．C．D．【考点】HK：由y=Asin（ωx+φ）的部分图象确定其解析式．【分析】由函数的图象的顶点坐标求出A、φ，由周期求出ω，可得函数的解析式．【解答】解：函数y=Asin（ωx+ϕ）（A＞0，ω＞0，|φ|＜），在同一周期内，时取得最大值，时取得最小值﹣，∴A=， =﹣，∴ω=3．再根据3•+φ=2kπ+，k∈Z，∴φ=，故函数的解析式为 y=sin（3x+），故选：B．二、填空题（每小题4分，共16分）13．求值：sin750°+cos（﹣660°）+tan（﹣135°）．【考点】GO：运用诱导公式化简求值．【分析】利用诱导公式可得sin750°+cos（﹣660°）+tan（﹣135°）=sin30°+cos60°+tan45°，从而可得答案．【解答】解：sin750°+cos（﹣660°）+tan（﹣135°）=sin（2×360°+30°）+cos（﹣2×36°+60°）+tan（﹣180°+45°）=sin30°+cos60°+tan45°=++1=2．14．函数的定义域是．【考点】33：函数的定义域及其求法．【分析】函数的定义域满足：2x+≠k，k∈Z，由此能求出函数的定义域．【解答】解：函数的定义域满足：2x+≠k，k∈Z，解得x≠+，k∈Z，∴函数的定义域是．故答案为：．15．已知，，且∥，则的坐标为（2，﹣4）或（﹣2，4）．【考点】96：平行向量与共线向量．【分析】设=（x，y），由，，且∥，利用向量的模的定义和向量平行的条件，列出方程组，能求出的坐标．【解答】解：设=（x，y），∵，，且∥，∴，解得或，∴=（2，﹣4）或=（﹣2，4）．故答案为：（2，﹣4）或（﹣2，4）．16．已知，，且，则在方向上的投影为﹣2 ．【考点】9R：平面向量数量积的运算．【分析】根据平面向量数量积公式求出•的值，再求在方向上的投影大小．【解答】解：，，且，∴4﹣4•﹣3=4×42﹣4•﹣3×32=61，解得•=﹣6，∴在方向上的投影为：||cosθ===﹣2．故答案为：﹣2．三、解答题（本题共6道大题，共56分）17．已知=（1，2），=（﹣3，2），当k= 19 时，（1）k+与﹣3垂直；当k= 时，（2）k+与﹣3平行．【考点】9T：数量积判断两个平面向量的垂直关系．【分析】由向量的坐标运算可得k+=（k﹣3，2k+2），﹣3=（10，﹣4），由垂直和平行关系分别可得k的方程，解方程可得答案．【解答】解：（1）∵=（1，2），=（﹣3，2），∴k+=（k﹣3，2k+2），﹣3=（10，﹣4）∵k+与﹣3垂直，∴10（k﹣3）﹣4（2k+2）=0，解得k=19；（2）由（1）知k+=（k﹣3，2k+2），﹣3=（10，﹣4）∵k+与﹣3平行，∴﹣4（k﹣3）=10（2k+2），解得k=﹣故答案为：19；．18．已知，是同一平面内两个不共线的向量，（1）如果=+， =2﹣， =4+，求证A、B、D三点共线；（2）试确定实数k的值，使和共线．【考点】96：平行向量与共线向量．【分析】（1）证明，共线即可；（2）利用向量共线定理和平面向量基本定理即可得出．【解答】（1）证明：∵ =，∴与共线，又与有公共点B，∴A，B，D三点共线；（2）解：∵若使和共线．∴存在实数λ，使得=λ（）成立，∴．∵，是同一平面内两个不共线的向量，∴，解得．∴实数k的值是±2．19．已知，是同一平面内两个单位向量，其夹角为60°，如果=2+， =﹣3+2．（1）求（2）求与的夹角．【考点】9R：平面向量数量积的运算；9S：数量积表示两个向量的夹角．【分析】（1）由已知=2+， =﹣3+2，直接展开得答案；（2）求出、的值，结合（1）中求出的，代入数量积求夹角公式得答案．【解答】解：（1）由已知得，cos＜＞=．∵=2+， =﹣3+2，∴=（2+）•（﹣3+2）=﹣6=﹣6+1×+2=；（2）==．=．设与的夹角为θ（0≤θ≤180°），则c osθ==．∴θ=120°．20．已知，（1）求tanα；（2）求sin2α+sinαcosα的值．【考点】GI：三角函数的化简求值．【分析】把已知等式两边平方，可得α∈（），求出sinα﹣cosα的值，与原式联立求得sinα、cosα的值．（1）直接由商的关系求得ta nα；（2）把分母中的“1”用平方关系代替，化弦为切求解．【解答】解：由，得，∴2sinαcosα=．∵0＜α＜π，∴α∈（），则sinα＞0，cosα＜0．则sinα﹣cosα==．联立，解得．（1）tan=；（2）sin2α+sinαcosα====．21．在△ABC中，M是线段AB的中点，，BN与CM相交于点E，设，，（1）用基底，表示和；（2）用基底，表示．【考点】9H：平面向量的基本定理及其意义．【分析】（1）根据向量加法的三角形法则表示；（2）设=x﹣， =y，用两种方法表示出，列方程组得出x，y即可表示出．【解答】解：（1）∵M是线段AB的中点，，∴=， =，∴=﹣+=﹣+，=﹣+=．（2）设=x﹣， =y，则==（）+x，又==y+（），∴，解得，∴=．22．已知函数（1）求f（x）的单调递增区间；（2）若x∈[0，2π]，求f（x）的值域．【考点】H5：正弦函数的单调性；HW：三角函数的最值．【分析】（1）利用正弦函数的单调性，求得f（x）的单调递增区间．（2）利用正弦函数的定义域和值域，求得f（x）的值域．【解答】解：（1）对于函数，令2kπ﹣≤+≤2kπ+，求得4kπ﹣≤x≤4kπ+，可得f（x）的单调递增区间为[4kπ﹣，4kπ+]，k∈Z．（2）当x∈[0，2π]， +∈[，]，∴sin（+）∈[﹣，1]，∴ sin （+）∈[﹣1，]，∴f（x）∈[0， +1]．。

《精编》宁夏石嘴山市高三数学第二次联考试题理新人教A版.doc

宁夏回族自治区石嘴山市2021届高三第二次联考数学试题〔理科〕全解全析一、选择题1．设集合(){|ln 1,}A x y x y R ==-∈，集合2{|,}B y y x x R ==∈，那么A B =〔〕A. φB. [0，1)C. (1，+∞)D.〔－∞，1〕【解析】因为{|10}{|1}A x x x x =->=<，{|0}B y y =≥，所以[0,1)AB =，应选择B 。

2．假设复数12ω=+〔i 为虚数单位〕，那么1ω-等于〔〕A. 2ωB. 2ω-C.ω-D.1ω-【解析】因为111122ω-=+-=-，2211()22ω==-+，所以21ωω-=，应选择A 。

3．公差不为零的等差数列{}n a 中，236,,a a a 成等比数列，那么其公比为〔〕A ．1B ．2C ．3D ．4【解析】设等差数列{}n a 的公差为d ，那么21a a d =+，312a a d =+，615a a d =+。

因为236,,a a a 成等比数列，所以2111()(5)(2)a d a d a d ++=+，化简得212d a d =-。

因为0d ≠，所以12d a =-，21a a =-，313a a =-，公比312133a a q a a -===-，应选择C 。

4．命题p ：m 、n 为直线，α为平面，假设m ∥n ，α⊂n ，那么m ∥α；命题q ：假设a ＞b ，那么ac ＞bc ，那么以下命题为真命题的是〔〕 A. p 或qB. ⌝p 或qC. ⌝p 且qD. p 且q【解析】假设m ∥n ，α⊂n ，那么m ∥α，也可能m α⊂，所以命题p 是假命题；假设a ＞b ，当0c =时，ac bc =；当0c <时，ac bc <，所以命题q 也是假命题，综上所述，p 或q 为假命题；⌝p 或q 为真命题；⌝p 且q 为假命题；p 且q 为假命题，应选择B 。

宁夏石嘴山市高二数学下学期第二次月考试卷文(含解析)(2021年整理)

宁夏石嘴山市2016-2017学年高二数学下学期第二次月考试卷文（含解析）编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（宁夏石嘴山市2016-2017学年高二数学下学期第二次月考试卷文（含解析））的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为宁夏石嘴山市2016-2017学年高二数学下学期第二次月考试卷文（含解析）的全部内容。

2016—2017学年宁夏石嘴山高二（下）第二次月考数学试卷（文科）一、选择题（共12小题，每小题5分，满分60分）1．已知集合A={x|x＞0｝,集合B=｛x|2≤x≤3}，则A∩B=（）A．[3，+∞) B．[2，3］C．（0,2］∪[3，+∞）D．（0,2]2．已知全集U=R,N={x|x（x+3）＜0｝，M={x|x＜﹣1}，则图中阴影部分表示的集合是（）A．｛x|﹣3＜x＜﹣1｝ B．｛x|﹣3＜x＜0} C．{x｜﹣1≤x＜0｝D．｛x｜x＜﹣3｝3．满足条件M∪｛1｝=｛1，2,3｝的集合M的个数是（）A．1 B．2 C．3 D．44．下列各组函数f（x）与g(x）相同的是（）A．f(x)=1，g（x）=x0B．f（x）=x2，g（x）=（x+1)2C．f（x）=x，g（x）=e lnx D．f（x）=|x｜，g（x）=5．若函数y=（x+1)（x﹣a）为偶函数，则a=（)A．﹣2 B．﹣1 C．1 D．26．已知a,b∈R，则“b≠0"是“复数a+bi是纯虚数”的（）A．充分而不必要条件 B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件7．已知复数z满足（z﹣5）（1﹣i）=1+i，则复数z的共轭复数为( ）A．5+i B．5﹣i C．﹣5+i D．﹣5﹣i8．下列函数中与函数y=﹣3|x｜奇偶性相同且在(﹣∞，0)上单调性也相同的是（）A．y=﹣B．y=log2|x｜ C．y=1﹣x2D．y=x3﹣19．设U=R，A={x｜mx2+8mx+21＞0},∁U A=∅，则m的取值范围是（）A．[0,）B．{0｝∪（，+∞）C．（﹣∞,0］D．（﹣∞，0]∪（,+∞)10．A、B为两个非空集合，定义集合A﹣B={x｜x∈A且x∉B｝，若A=｛﹣2，﹣1，0，1，2}，B={x|（x﹣1）（x+2)＜0｝，则A﹣B=（）A．{2｝B．｛1，2} C．{﹣2,1,2} D．{﹣2，﹣1，0}11．曲线C的参数方程为（α为参数)，M是曲线C上的动点，若曲线T极坐标方程2ρsinθ+ρcosθ=20,则点M到T的距离的最大值( ）A．B．C．D．12．已知函数f（x)是定义在R上的偶函数，且对任意的x∈R，都有f（x+2）=f（x)．当0≤x≤1时，f（x）=x2．若直线y=x+a与函数y=f(x）的图象在[0,2］内恰有两个不同的公共点，则实数a的值是( ）A．0 B．0或 C．或D．0或二、填空题13．函数f（x）=x2+2（a﹣1）x+2在区间（﹣∞，4］上递减，则实数a的取值范围是．14．已知函数f（x）=若f（1）+f（a）=2,则a的值为．15．已知定义在R上的奇函数f(x），当x＜0时,f(x）=2x﹣3．若f（a）=7，实数a的值是．16．给出下列四个命题：①“若x+y≠5，则x≠2或y≠3”是假命题；②已知在△ABC中，“A ＜B”是“sinA＜sinB”成立的充要条件；③若函数，对任意的x1≠x2都有＜0,则实数a的取值范围是；④若实数x，y∈[﹣1，1]，则满足x2+y2≥1的概率为．其中正确的命题的序号是(请把正确命题的序号填在横线上）．三。

宁夏石嘴山市第三中学高一数学12月月考试题(无答案)(2021年整理)

编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（宁夏石嘴山市第三中学2017-2018学年高一数学12月月考试题（无答案））的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为宁夏石嘴山市第三中学2017-2018学年高一数学12月月考试题（无答案）的全部内容。

一．选择题（共12题，每题5分)1。

下列说法中正确的个数为（）①正棱锥的所有侧棱相等；②直棱柱的侧面都是全等的矩形；③圆柱的母线长都相等；④用经过旋转轴的平面截圆锥，所得的截面一定是等腰三角形．A．4 B．3 C．2 D．12．下列说法中正确的个数是( ）①角的水平放置的直观图一定是角. ②相等的角在直观图中仍然相等.③相等的线段在直观图中仍然相等.④若两条线段平行,则在直观图中对应的两条线段仍然平行。

A.1B.2 C。

3 D。

43．棱长都是1的三棱锥的表面积为( ）视图A。

3 B 。

23 C. 33 D。

434．若一个三角形，采用斜二测画法作出其直观图，则其直观图的面积是原三角形面积的（）A.错误!倍 B．2倍 C。

错误!倍 D.错误!倍5、下列说法正确的是（)A、三点确定一个平面B、四边形一定是平面图形C、梯形一定是平面图形D、平面α和平面β有不同在一条直线上的三个交点6．一个简单几何体的主视图、俯视图如图所示，则其左视图不可能为（)A。

正方形 B．圆 C．等腰三角形 D．直角梯形7、平面α与平面β平行的条件可以是（）A.α内有无穷多条直线与β平行;B.直线a//α，a//β8．如下图左1111ABCD A B C D 是长方体,O 是11B D 的中点,直线1A C 交平面于11AB D 点M ，则下列结论错误．．的是( ) A ．,,A M O 三点共线 B ．1,,,M O A A四点共面C ．1,,,B B O M 点共面D ．,,,A O C M9.《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺。

2018-2019学年宁夏石嘴山市第三中学高一下学期期末考试数学试题

2018-2019学年宁夏石嘴山市第三中学高一下学期期末考试数学试题本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分，考生作答时，将答案写在答题卡上，在本试卷上答题无效。

第I 卷（选择题）一选择题（本大题共60分,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的）． 1．=45tanπ（） A ．22-B ．22 C ．-1 D ．1 2．已知扇形的弧长是8，其所在圆的直径是4，则扇形的面积是（）A ．8B ．6C ．4D ．163．已知向量(),1a k =-，()3,4b =-，如果向量2a b +与3a b -平行，则实数k 的值为（）A ．14B ．34C ．14-D ．34-4．已知角α的终边上有一点P （32sinπ，32cos π），则tan α=（） A ．33-B ．33C ．3-D ．3 5．已知)20(552sin παα<<=，则=-)4tan(πα( )A ．-3B ．31-C ．31D ．3 6．已知DEF 、、分别是ABC ∆的边BC CA AB 、、的中点，则①12EF BC =；②EA BE BC=-；③AD BE CF +=-中正确等式的个数为（） A ．0 B ．1 C ．2 D ．37.已知函数f(x)＝Asin(ωx ＋φ为( )8．已知向量a ，b 满足3a b -=且()0,1b =-，若向量a 在向量b 方向上的投影为2-，则a =A ．2B ．．4 D ．12 9．函数 )2,2(tan cos ππ-=x x y 的大致图象是（）A ．B ．C ．D ．10．将函数⎪⎭⎫⎝⎛+=32sin )(πx x f 的图象向左平移m (0)m >个单位长度,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数()g x 的图象,若对任意的x ∈R 均有()12g x g π⎛⎫≤ ⎪⎝⎭成立,则m 的最小值为（）A ．2324πB ．1211πC ．12π D ．24π 11．如图，平行四边形ABCD 的对角线相交于点O ，E 是OD 的中点，AE 的延长线与CD 相交于点F 若，3,2,1===BD AB AD ，则=⋅BD AF ( )A ．23 B ． -1 C ． 33D ． 32-12．已知函数)(cos sin )(R a x a x x f ∈+=图象的一条对称轴是 6π=x ，则函数)(sin 2)(x f x x g ⋅=的最大值为（）A ．5B ． 3C ．5D ．3第II 卷（非选择题)二填空题（本大题共20分,每小题5分）．13．已知()()1,,,1a cosa b sina ==，若a b ⊥，则sin2α=14.函数y ＝b+asinx （a<0）的最大值为–1，最小值为–5，则y ＝tan （3a+b ）x 的最小正周期为15．如图，半径为1的扇形AOB 的圆心角为 120，点C 在B A上，且 30=∠COA ，若OB OA OC μλ+=，则=+μλ__________.16．下列结论中：① 350tan 10tan 350tan 10tan =++ ② 函数tan 26y x π⎛⎫=+⎪⎝⎭的图像关于点,012π⎛⎫⎪⎝⎭对称 ③ 函数cos 23y x π⎛⎫=+⎪⎝⎭的图像的一条对称轴为23x π=-④ 1)10tan 31(40cos =+其中正确的结论序号为____________________．三解答题（本大题共70分）．17．（本题10分）已知 21,e e 是夹角为 60的单位向量，且，212123,2e e e e +-=+= （1）求⋅；（2）求与的夹角θ。

2023-2024学年宁夏六盘山高一下学期第二次月考数学模拟试题(含解析)

AD
15
3
（
0
≤
≤1
），
3
3
3
22
当 1时， AE AF 取得最大值为 6.
方法 2：由题意知， AC BD ，则分别以 AC、BD 所在直线为 x 轴、y 轴建立平面直角坐标系，如
图所示，
则
A(
3 2
,
0)
，
B(0,
3
3 2
)
，
C
(
3 2
,
0)
，
D(0,
3
3 2
)
，
又因为 BC 3BE ，
其中 AB 3 ， BC 4 ， PA 5 3 ，
则长方体的外接球和三棱锥 P ABC 的外接球为同一个球，
设外接球的半径为 R ，可得 2R 32 42 5 3 2 10 ，得 R 5 ，
所以三棱锥 P ABC 的外接球的体积为V 4 π 53 500 π .
3
3
故选：C.
故选：C.
7．B
【分析】根据分层抽样平均数的计算方法计算该校教师平均微信步数
【详解】因为分层随机抽样是按比例分配，所以根据公式得该校教师平均微信步数为
160 160 140
×12500＋
140 160 140
×8600＝10680.
故选：B
8．D
【分析】根据圆柱、圆锥、球体的表面积公式即可求解. 【详解】对 A，圆柱的侧面积等于 2πR 2R 4πR2 ,正确；对 B，球面面积为 4πR2 ，所以圆柱的侧面积与球面面积相等，B 正确；
故
S ABC
1 11 2
1, 2
根据直观图面积和原图面积之间的关系式 SABC

宁夏石嘴山市高一下学期数学第二次月考试卷

高一下学期数学第二次月考试卷

宁夏石嘴山市高一数学下学期期中试卷(含解析)

宁夏高一数学下学期第二次月考试卷(含解析)

高一下学期第二次月考数学试题(含答案)

2023-2024学年宁夏回族自治区石嘴山市平罗县高一下册3月月考数学试题(含解析)

宁夏石嘴山市高三数学第二次联考试题 理 新人教A版

宁夏石嘴山市第一中学2025届高三第二次联考数学试卷含解析

宁夏高一下学期数学第二次月考试卷

宁夏石嘴山市高一数学下学期第二次(5月)月考试题(扫描

宁夏石嘴山市第三中学高一数学上学期第二次考试试题

宁夏石嘴山市高一数学下学期第二次(5月)月考试题(扫描版)

宁夏高一数学下学期第二次月考试卷(含解析)

《精编》宁夏石嘴山市高三数学第二次联考试题 理 新人教A版.doc

宁夏石嘴山市高二数学下学期第二次月考试卷 文(含解析)(2021年整理)

宁夏石嘴山市第三中学高一数学12月月考试题(无答案)(2021年整理)

2018-2019学年宁夏石嘴山市第三中学高一下学期期末考试数学试题

2023-2024学年宁夏六盘山高一下学期第二次月考数学模拟试题(含解析)

宁夏石嘴山市高三数学第二次联考试题理新人教A版

《精编》宁夏石嘴山市高三数学第二次联考试题理新人教A版.doc

宁夏石嘴山市高二数学下学期第二次月考试卷文(含解析)(2021年整理)