高等几何讲义 第二章射影平面____§1 扩大仿射平面
大学高等几何授课讲义

• 2、已知仿射变换
x/ 2x y 1
• 求点 P1(1, 0), P2 (1, 0)
y/
x
y
3
• 的像点,及直线 x y 2 0的像直线。
第一章、仿射坐标与仿射变换
复习仿射坐标 及代数表示式
• 正交变换
x'
y
•
所以:
x'
y'
a11x a21x
a12 y a13 a22 y a23
第一章、仿射坐标与仿射变换
例 已知三点 O(0,0), E(1,1), P(1, 1)求仿射变换T使顺次 变为 O1(2,3), E1(2,5), P1(3, 7).
• 练习:1、求使直线x 0, y 0, x 2y 1 0分别变
点集拓扑 代数拓扑 解析拓扑
分形几何
微分拓扑 微分流形 纤维丛
五、课程简介
• 周学时3,一个学期,学习第一章~第六章
• 主要参考书:
•梅向明、门淑惠等编《高等几何》,高等教育出版社出版, 2008年; • 朱德祥、朱维宗等编《高等几何》(第二版),高等教育出 版社出版,2010年; •罗崇善编《高等几何》,高等教育出版社出版,1999年6月; •朱德祥、李忠映、徐学钰等编《高等几何习题解答》。
x' y'
A
x y
a b
,
直线l1
:u
u1
u2
,l2
:vΒιβλιοθήκη v1v2l1
//
l2
u
v即
u1 u2
v1 v2
u1' u2'
A
u1 u2
[高等教育]射影平面
![[高等教育]射影平面](https://img.taocdn.com/s3/m/8b526b3c48d7c1c708a14594.png)
4、每一组平行平面有且仅有一条交线为无穷远直线;过同一 条无穷远直线的平面相互平行. 因而,对于通常平面:
平行
无穷远直线
两平面
交于惟一
不平行
有穷远直线
空间中任二平面必相交于唯一直线
§ 2.1 射影平面
三、射影平面
定义1.24 通常点和无穷远点统称拓广点; 添加无穷远点后的直线和无穷远直线统称为拓广直线(射影仿 射直线); 添加无穷远直线后的平面称为拓广平面(射影仿射平面).
§ 2.1 射影平面
(2) 拓广直线的拓扑模型
§ 2.1 射影平面
(3) 射影直线上点的分离关系
欧氏直线:一点区分直线为两个部分。 射影直线:一点不能区分直线为两个部分。 欧氏直线:两点确定直线上的一条线段。 射影直线:两点不能确定直线上的一条线段。
点偶A,B分离点偶C,D
点偶A,B不分离点偶C,D
平行
无穷远点
两直线 不平行 交于惟一 有穷远点
平面上任二直线总相交
5、空间中每一组平行直线交于惟一无穷远点. 6、任一直线与其平行平面交于惟一无穷远点.
§ 2.1 射影平面
理解约定1.1(3)
1、无穷远直线为无穷远点的轨迹. 无穷远直线上的点均为无穷 远点;平面上任何无穷远点均在无穷远直线上.
2、每一条通常直线与无穷远直线有且仅有一个交点为该直线 上的无穷远点.
§ 2.1 射影平面
一、中心射影
2、平面到平面的中心射影
定义1.23 : '
O投射中心(O ')
OP 投射线 P' π 上的点P 在π'上的像 P π' 上的点P'在π上的像
高等几何 总复习

a 2 (b c ) d 0,
一维射影变换的分类:
(ad bc 0)
( 2)
相异实根 相异实二重元 双曲型 0 0 (2)有两个相同实根 (1)有两个相同实二重元 称为 抛物型 0 共轭虚根 共轭虚二重元 椭圆型
18
第三章 一维射影几何学
a1 a2
b1 b2
0
( 2 2 ) 1
相应几何学 基本不变性质
射影几何 结合性
仿射几何 平行性
欧氏几何 合同性
基本不变量
基本不变图形
交比
---------
简比
无穷远直线
距离、角度
无穷远直线
29
复习题
1. 无三点共线的______对对应点决定唯一的二维射影变换 2. 当射影变换使无穷远直线不变、两个虚圆点也不变时,射影变换就是 A.正交变换 B.正相似变换 C.反相似变换 D. 运动变换 3.射影坐标系下,坐标三角形A1A2A3 ,单位点E,顶点A3坐标_______ A1A2方程_____, A1E的坐标_____. 判断题 1.二维射影变换有双曲型、抛物型、椭圆型 ( ) 2.简比是射影不变量 ( )
2.射影对应间的关系: 透视 射影
对合
重叠的一维几何形式 S 2 I ( S S 1 ), S I
3.一维射影几何研究的方法
代数方法:工具是交比:两个一维几何图形成射影对应 的充要条件是:对应四元素交比相等. 几何方法:工具是射影: 将射影分解为有限个透视之积(见§3.5).
目前已知的射影性质:
射影不变性: 结合性:某点在某直线上;某直线通过某点的事实保持不变 同素性:点 点;直线 直线
14
大学高等几何课件第二讲

定理1.7 给定平面内的两个三角形,至多利用三回透视仿射可 使一个三角形变为另一个三角形。
经过仿射变换可以相互转换的图形称为是仿射等价的。 所以任意两个三角形是仿射等价的。直线、四边形也是仿 射等价的。
平面仿射几何基本定理:设P1,
P 2
,
P 是平面内不共线的 3
中心投影:设 f : 是平面到平面 的一一点对应, 且满足对应点的连线通过一个定点,则称 f 是从平面 到 平面 的中心投影.
问题:中心投影是不是数学意义下的一一对应? 分析:当照射光线OP0与l平行时, P0在l上的投影不存在,而引 起P0的投影不存在的原因是平行没有交点这一约定. 解决办法: 取消平行线没有交点的限制,在直线上引进"新点".
(1) 空间中任何一组平行直线有且仅有一个公共的点 无穷远点.
(2) 一直线与它的平行平面交于一个无穷远点. (3) 一组平行平面相交于一条无穷远直线.
仿射直线与射影直线 仿射直线(平面):引入了无穷远点的欧氏直线(平面)称为
仿射直线(平面). 射影直线(平面): 将仿射直线(平面)上的无穷远点与通常的
无穷远元素 规定1: 在平面内对任何一组平行线引进唯一一点叫做无穷远 点(记作P )与之对应,此点在组中的每一直线上,而不在组外的 任何直线上. 规定2: 平面内无穷远点的集合是一条无穷远直线,记作l. 规 定 3 : 空间中所有无穷远点的集合是一个平面,叫做无穷远平
面, 记做 .
在这些规定下, 可以证明 :
a
2经过伸缩变换
y
b a
(a y,
0, b
2.1射影平面

§ 1 射影直线和射影平面
定义1.5 如果把仿射直线上的非无穷远点与 无穷远点同等看待而不加区分那么这条直线就 叫做射影直线
圆
墨比乌斯带
定义1.6 在仿射平面上,如果对于普通元素和 无穷远元素不加区分,即可得到射影平面
§ 1 射影直线和射影平面
五、射影直线、射影平面的基本性质
1、射影直线
欧氏直线:一点区分直线为两个部分。
§ 1 射影直线和射影平面
1.4 德萨格(Desargues)定理 应用举例
例2 证明:三角行的三中线点共.
§ 1 射影直线和射影平面
1.4 德萨格(Desargues)定理
今 天 作 业
P28 : 5
O投射中心(O l l ')
OP 投射线 P' l 上的点P在l'上的像 P l' 上的点P'在l上的像 因此 ,φ–1: l' → l是 l' 到 l 的中心射影 三个特殊的点: X=l×l' 自对应点(不变点) OU与l'不相交, U为l上的影消点 OV'与l不相交, V'为l'上的影消点 影消点的存在,导致两直线间的中心射影不是一个一一对应
§ 1 射影直线和射影平面
1.4 德萨格定理
德萨格(Desargues)定理
如果两个三点形对应顶点的连线交于 一点,则对边的交点在一直线上.
A
X
C
Y
C
B
A
B Z
O
A
X
C
B Z Y
C
B
A
o
L
A
l
L
A
X
C
高等几何仿射坐标与仿射变换

a 11
原象点: A,B,C,D…… 直线a上的点
映象点:A, B,C, D…… 直线上 a 的点 平行射影的方向:直线 l
记透视仿射对应T: T A A,T B B ………
透视仿射对应与方向有关,方向变了,则得到另外的透视仿射
对应
D
a
C
l
A
B
O A B C D
a
点 O 为自对应点( 同一平面上两相交直线的公共点 ) 12
CB
10
二.两直线间透视仿射对应、仿射对应与仿射变换
1..两直线间的透视仿射对应
≠ ≠
点若A直,B线,C,aD,…a… a,,l过点A,B,且C,Dl…作a直线, ll的平行a线交, a于
A, B,C, D……,则可得直线 a 到直线 a的一个映射。
称为透视仿射对应,记为 T D
a
l AB C
A B C D
1.透视仿射对应: 如图
点A,B,C共线a,则 A, B,C 共线 a
T A A T B B T C C g
C a l
B A
T a a
A B
两相交平面的交线为自对应点的集合即对应轴 C
a
15
第一章、仿射坐标与仿射变换 如图
16
2仿射对应:平面到平面的仿射对应是有限次透视仿射对应的 积组成的,是透视仿射对应链。
2.两直线间的仿射对应
T Tn T 1 n2
T2T1
仿射对应是透视仿射对应链或平行射影链
T1,T2, Tn2 ,Tn1 表示透视仿射链,T表示仿射对应 (如图)
A1
B1
C1
A2
B2
C2
l2
A3 B3
C3
第二章射影平面
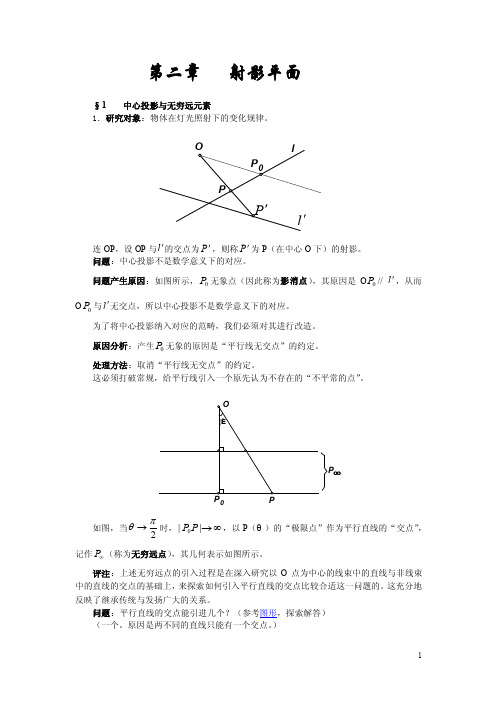
第二章 射影平面§1 中心投影与无穷远元素1.研究对象:物体在灯光照射下的变化规律。
连OP ,设OP 与l '的交点为P ',则称P '为P (在中心O 下)的射影。
问题:中心投影不是数学意义下的对应。
问题产生原因:如图所示,0P 无象点(因此称为影消点),其原因是O 0P // l ',从而O 0P 与l '无交点,所以中心投影不是数学意义下的对应。
为了将中心投影纳入对应的范畴,我们必须对其进行改造。
原因分析:产生0P 无象的原因是“平行线无交点”的约定。
处理方法:取消“平行线无交点”的约定。
这必须打破常规,给平行线引入一个原先认为不存在的“不平常的点”。
如图,当2πθ→时,∞→||0P P ,以P (θ)的“极限点”作为平行直线的“交点”,记作∞P (称为无穷远点),其几何表示如图所示。
评注:上述无穷远点的引入过程是在深入研究以O 点为中心的线束中的直线与非线束中的直线的交点的基础上,来探索如何引入平行直线的交点比较合适这一问题的。
这充分地反映了继承传统与发扬广大的关系。
问题:平行直线的交点能引进几个?(参考图形,探索解答) (一个。
原因是两不同的直线只能有一个交点。
)o o无穷远点的引进是一个创新的过程,需要大胆的想象力。
而直线上的无穷远点只能引进一个则是原来的原则“两直线只有一个交点”的要求所至。
无穷远点根据研究需要而引入,又是原系统的规则的延伸,从而“无穷远点”又受到原系统的规则的“约束”,这充分体现了继承与发展的关系。
对照一维中心投影,请自行考虑二维中心投影的相应问题。
2. 无穷远元素规定一 在平面内对任何一组平行线引入唯一一点叫做无穷远点(记作∞P )与之对应,此点在组中每一直线上而不在组外的任何直线上。
规定二 平面内无穷远点的集合是一条直线,叫做无穷远直线,记作∞l 。
规定三 空间里所有无穷远点的集合是一个平面,叫做无穷远平面,记作∞π。
21射影平面

如果两个三点形对应边的交点在一直线上,则 对应顶点的连线交于一点.
定义1.11 如果两个三点形对应边的交点共线,则
这条直线叫做透视轴.如果两个三点形对应 顶点的连线共点,则这个点叫做透视中心.
§ 1 射影直线和射影平面
1.4 德萨格(Desargues)定理
应用举例
例1 在欧氏平面上, 设ΔABC的高线分别为 AD, BE, CF. 而 BC×EF=X, CA×FD=Y, AB×DE=Z. 求证:X, Y, Z三点共线.
约定 (2)一平面内一切无穷远点的集合组成一条直线叫做 无穷远直线,记作l∞,区别起见,称平面上原有的直线为有穷 远直线(通常直线)
约定 (3) 空间里一切无穷远点的集合组成一个平面叫做无穷 远平面,记作π∞,为区别起见,空间里原有平面称为非无穷远平 面或普通平面.
总结:在平面上添加无穷远元素之后,没有破坏点与直线 的关联关系,同时使得中心射影成为一一对应.
§ 1 射影直线和射影平面
理解约定 (1), (2)
1、对应平面上每一方向,有惟一无穷远点. 平行的直线交于同 一无穷远点;交于同一无穷远点的直线相互平行.
2、每一条通常直线上有且仅有一个无穷远点.
3、不平行的直线上的无穷远点不同. 因而,对于通常直线:
平行
无穷远点
两直线 不平行 交于惟一 有穷远点
§ 1 射影直线和射影平面
一、中心射影
定义1.1 : l l'
2、平面到平面的中心射影
定义1.2 : '
均不是一一对应
中心射影不是一一对应的原因:存在影消点、影消线 存在影消点、影消线的原因:平行的直线没有交点
如何使得中心射影成为一个一一对应?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§1. 扩大仿射平面
a2 a3 b1 b2 b3 = 0. c1 c2 c3
证明:若有至少二点相同,则显然成立.
不同三点共线 存在直线 A1x1 A2x2 A3x3 0, 使三点坐标均满足此方程,即关于 A1、A2、A3 的 齐次线性方程组
高 等 几 何 ( Higher Geometry )
§1. 扩大仿射平面
➢2. 点的齐次仿射坐标
➢ 定义 设 = [O; e1, e2 ]是平面仿射坐标系.在
之下,满足下述条件的有序实数组 (x1, x2, x3) (0, 0, 0) 称为平面上点的齐次仿射坐标:
1.若 0,则 ( x1, x2, x3) 与 (x1, x2, x3)为同
高 等 几 何 ( Higher Geometry )
§1. 扩大仿射平面 ➢ 引入了无穷远点的平面称为扩大(仿射)平面,
引进了无穷远点的直线称为扩大直线. ➢ 注意:扩大仿射平面作为点的集合已不再是原
来的作为点集的仿射平面或欧氏平面.
高 等 几 何 ( Higher Geometry )
§1. 扩大仿射平面
M
/
/
§1. 扩大仿射平面
➢ 另外,中心射影不是双射.(如上图中的点 M;
再如下图中,直线间的中心射影下,点 P 无对
应点)
S
Q/ /
P
M
P/
M/
Q 分析(原因):平行直线无交点;平行平面无交线.
➢ 方法:引入无穷远元素,使中心射影成为双射.
➢ 新问题:无穷远元素如何表示?
高 等 几 何 ( Higher Geometry )
➢3. 直线的齐次仿射坐标方程
➢ 仿射坐标系下,直线的方程为
Ax By C 0.
➢ 扩大直线的齐次仿射坐标方程为:
Ax1 Bx2 Cx3 0 (A、B、C不全为0). (1)
➢ 无穷远直线: x3 0 .
(2)
➢ 例.设 0 为非无穷远直线, 0 为无穷远直
线,则 0 (, 为参数)表示什么图形?
第二章 射影平面____§1. 扩大仿射平面
➢1.中心射影
S
D
A
/
/ C/ B(B/) A/
D/
/
C
设 与 /是二相交平面,S 是不在 和 /上的一定 点,取作射影中心.对上的任意点 A,作直线SA 交 /于 A/.将点 A/ 称作点 A 在 /上的中心射影,
从中心 S 引出的直线 SA 称为投射线.
§1. 扩大仿射平面
➢无穷远元素的坐标表示
➢ 分析:平面仿射坐标系下,二直线
(1): A1x + B1y + C1 = 0,(2): A2x + B2y + C2 = 0,
若相交,则交点坐标为:
B1 C1 C1 A1 B2 C2 , C2 A2 . A1 B1 A1 B1 A2 B2 A2 B2
注意:此坐标与比值 B1 B2
➢ 可见,方向数与无穷远点一一对应. ➢ 几个结论:
1. 每一普通直线上有且仅有唯一无穷远点; 2. 平行直线有同一无穷远点; 3. 不平行直线有不同无穷远点; 4. 两点确定唯一直线. ➢ 符号约定: 齐次坐标为 (x1, x2, x3) 的点记为 x; 点x的任一组确定的齐次坐标记为(x) (x1, x2, x3).
答:为一束平行直线.
➢ 直线(1)上的无穷远点为(B, A, 0).
当直线平行于y轴时,其无穷远点可写为(0,1,0);
当不平行于 y 轴时,无穷远点可写为 (1,A/B,0).
高 等 几 何 ( Higher Geometry )
§1. 扩大仿射平面
➢ 因 k A/B 是直线 (1) 的方向数,故 方向数为 k 的直线上的无穷远点为 (1, k, 0); 方向数为 的直线上的无穷远点为 (0, 1, 0).
则有 x1 x2 x2 2 3 1 0, 1 40
故所求直线方程为:4x1 x2 5x3 0.
高 等 几 何 ( Higher Geometry )
§1. 扩大仿射平面
➢ 一般地,记 a、b所连直线为 a b,其坐标方程为
x1 x2 x3 a1 a2 a3 0. b1 b2 b3
其参数方程为:
一点的齐次仿射坐标;
2.若 x3 0,则 (x1, x2, x3)是(非齐次)仿射坐标为 x = x1/x3 , y = x2/x3 的普通点的齐次仿射坐标; 3.齐次仿射坐标为(x1,x2,0)的点称为无穷远点. ➢ 注意:条件 2 给出了普通点的(非齐次)仿射坐标 与齐次仿射坐标之间互化的方法.
C1 C2
:
C1 C2
A1 A2
:
A1 A2
B1 B2
是一一对应的.
注意到,所谓坐标不外乎点与数组之间的一种双
射,因此也可将此比值定义为点的一种坐标.
高 等 几 何 ( Higher Geometry )
§1. 扩大仿射平面 ➢ 另外,注意到当一组直线平行于固定方向时,其
中任二直线的三数比值中,前两数比值不变而第 三数为零,且另一组平行直线的此种比值与之必 不同. ➢ 可见此类三数比值与平行直线上的无穷远点是一 一对应的,因而可作为无穷远点的一种坐标.
a1A1 a2A2 a3A3 0
b1A1 b2A2 b3A3 0
有非零解
a1 b1
a2 b2
a3 b3
0.
c1A1
c2A2
c3A3
0
c1 c2 c3
高 等 几 何 ( Higher Geometry )
§1. 扩大仿射平面 ➢ 注:在代数观点下,可说
三点共线 此三点的坐标三数组线性相关. ➢ 例2 求点 a (2, 3, 1)、b (1, 4, 0) 确定的直线. ➢ 解:设a、b确定的直线上的动点为 x( x1, x2, x3 ),
x1 x2
a1 a2
b1 b2,、
R
且
2
2
0.
x3
a3
b3
或 (x) (a) (b),、 R 且 2 2 0.
高 等 几 何 ( Higher Geometry )
➢ 中心射影具有性质: 1. 将点变成点; 2. 将直线变成直线; 3. 保持点与直线的结合关系.
➢ 这是平行射影也具有的性质. ➢ 但中心射影不保持平行性,这
与平行射影不同!(如图)
S
/
高 等 几 何 ( Higher Geometry )
§1. 扩大仿射平面
