第二节 刚体转动的动能定理
刚体动能定理

m、L 、
θ
mg θ
即: 0 = Ep2 +Ek2
∴ω = 3g cosθ L
c
mg
Hc
θ
c
mg
人 杆
O M=70kg H=1.8m Hc =1.2m JM=70kgm2
m=27kg L=12m Hc =1.2m Jm =363kgm2 Jm ~5JM
Hc(M+m)g=(1/2)J ω2 +(M+m)gHccos θ
§3 — 3 力矩作功 刚体绕定轴转动的动能定理 一、力矩作功 1. 刚体中的内力不作功
W =0 内
因为刚体中各质元间无相对位移。 因为刚体中各质元间无相对位移。
r r dW = F ⋅ dr = F cos(90 −α)dS
0
2.力矩作功 力矩作功
α
dθ θ F ds
P
r θ
= Fsin αdS = Fsin αrdθ = Mdθ
ri
刚体的 转动动能
1 2 2 Ek = ∑Eki = ∑( ∆mi ri ω ) 2 i i
1 1 2 2 = (∑∆mi ri )ω = Jω2 2 i 2
2.动能定理 动能定理
dω dW = Mdθ = J dθ = Jωdω dt
W =∫
ω2 ω1
1 1 2 2 Jωdω = Jω2 − Jω1 2 2
X
处在重力场中的刚体, 处在重力场中的刚体,其重力势能 就是它的各质元重力势能的总和。 就是它的各质元重力势能的总和。
四、机械能守恒定律
在刚体的绕定轴转动中, 在刚体的绕定轴转动中,如果仅有保守内 力作功,则刚体的机械能守恒。 力作功,则刚体的机械能守恒。
刚体旋转知识点归纳总结

刚体旋转知识点归纳总结1. 刚体旋转的基本概念刚体是指在一定时间内,其内部各点的相对位置不改变的物体。
刚体旋转是指刚体围绕固定点或固定轴发生的旋转运动。
在刚体旋转中,需要引入一些基本概念:1.1 刚体的转动刚体的旋转可以是定点转动,也可以是定轴转动。
在定点转动中,刚体绕固定点旋转,而在定轴转动中,刚体绕固定轴旋转。
定点转动和定轴转动都是刚体旋转运动的两种基本形式。
1.2 刚体的转动角度和角速度刚体的转动角度是刚体在单位时间内所转过的角度,通常用θ表示。
刚体的角速度是指刚体单位时间内转过的角度,通常用ω表示。
在刚体定点转动中,角速度是刚体绕定点旋转的角度速度;在刚体定轴转动中,角速度是刚体绕定轴旋转的角度速度。
1.3 刚体的转动惯量刚体的转动惯量是衡量刚体抵抗旋转的惯性大小,通常用I表示。
刚体转动惯量的大小取决于刚体形状、质量分布以及旋转轴的位置。
对于质点组成的刚体,其转动惯量可以通过对质点的质量进行积分得到。
1.4 刚体的角动量刚体的角动量是刚体旋转运动的物理量,通常用L表示。
角动量的大小和方向分别由角速度和转动惯量决定。
在定点转动中,如果刚体的角速度和转动惯量都不变,那么刚体的角动量也保持不变;在定轴转动中,如果刚体绕固定轴旋转,那么刚体的角动量也保持不变。
2. 刚体的转动力学刚体的转动力学研究刚体在旋转运动中所受的力和力矩,包括转动定律、角动量定理、动能定理等内容。
2.1 刚体的平衡刚体旋转平衡需要满足一定的条件,包括力矩平衡条件和动量平衡条件。
刚体力矩平衡条件是指刚体所受的合外力矩为零;刚体动量平衡条件是指刚体所受的合外力矩关于某一点的力矩为零。
2.2 刚体的角动量定理刚体的角动量定理描述了刚体在受到外力矩作用下,其角动量的变化规律。
根据角动量定理,刚体所受外力矩产生的角动量变化率等于刚体所受外力矩的矢量和。
2.3 刚体的动能定理刚体的动能定理描述了刚体在旋转运动中,其动能的变化规律。
根据动能定理,刚体所受外力矩产生的功率等于刚体动能的变化率。
刚体转动的动能定理

一、力矩的功 1 力矩的定义若作用的质点上的力为F ,则将r ×F 定义为力F 对O 点的力矩,记为M 。
M r F =⨯M 、F 、r 三者的方向构成右手螺旋关系。
M大小:方向:右手法则2 力矩的功设:;转盘上的微小质量元Δm 在力F 作用下以R 为半径绕O 轴转动,在dt 时间内转过角度d ,对应位移d r,路程ds,此时F 所做的元功为则总功为二、转动惯量设初速为零,质量元Δm 的动能为转盘的总动能1 定义:为物体的转动惯量。
意义:由质量和质量对于转轴的分布情况决定。
描述转动的惯性。
o z FtF nF tF ord rd θt t d d d d A F r F s F r θ=⋅==d d A M θ=21d A M θθθ=⎰αrsin t M Fr F rα==d θFtF ord r12ki i iE m v =212k ki i i i i E E m ==∆∑∑v 221()2i i i m r ω=∆∑2i i iI m r =∆∑单位:SI 制 kg m 22 定轴转动物体转动惯量的计算质量不连续分布的质点系:转动惯量定义为各个质点对该定轴的转动惯量之和2i i iI m r =∑质量连续分布的刚体:转动惯量定义为各个质点对该定轴的转动惯量的积分。
2mI r dm =⎰转动惯量的大小不仅取决于物体的质量,还与质量的分布和轴线的位置有关。
例1 求小球m 的转动惯量。
解:m 看作质点 I = m R 2例2 质量为m 的细圆环,求I 。
解:把环分成无限多个质量为dm 的小段,对每个d m 有d J = R 2对整个环有I = R 2d m = mR 2例3质量m ,半径 R 的薄圆盘,求I 。
解:把盘分成无限多个环。
取其中的一个环(半径r ,宽d r ,质量 d m ), 其转动惯量 d I = r 2d m22mdm rdr Rππ=整个盘的转动惯量d rd md SrRd mRRm22322200002122R R R Rm m I dI r dm r rdr r dr mR R R ππ=====⎰⎰⎰⎰例4 长为L 、质量为m 的细长直杆,转轴垂直于细杆且通过杆中心 解:杆长为L,质量为m, 则密度为=m / L 。
第二节 刚体转动的动能定理

§ 3.2 刚体转动的动能定理一、力矩的功 1 力矩的定义若作用的质点上的力为F ,则将r ×F 定义为力F 对O 点的力矩,记为M 。
M r F =⨯M 、F 、r 三者的方向构成右手螺旋关系。
大小:方向:右手法则2 力矩的功设:;转盘上的微小质量元Δm 在力F 作用下以R 为半径绕O 轴转动,在dt 时间内转过角度d θ, 对应位移d r,路程ds,此时F 所做的元功为则总功为二、转动惯量设初速为零,质量元Δm 的动能为转盘的总动能1 定义:为物体的转动惯量。
FtF nF tF d rt t d d d d A F r F s F r θ=⋅==d d A M θ=21d A M θθθ=⎰αrsin t M Fr F rα==tF d r12ki i iE m v =212k ki i i i i E E m ==∆∑∑v 221()2i i i m r ω=∆∑2i i iI m r =∆∑意义:由质量和质量对于转轴的分布情况决定。
描述转动的惯性。
例:一头粗,一头细的杆以不同端作轴转动是,其转动惯量不同。
单位:SI 制 kg m 22 定轴转动物体转动惯量的计算 质量不连续分布的质点系:转动惯量定义为各个质点对该定轴的转动惯量之和2i i iI m r =∑质量连续分布的刚体:转动惯量定义为各个质点对该定轴的转动惯量的积分。
2mI r dm =⎰转动惯量的大小不仅取决于物体的质量,还与质量的分布和轴线的位置有关。
例1 求小球m 的转动惯量。
解:m 看作质点 I = m R 2例2 质量为m 的细圆环,求I 。
解:把环分成无限多个质量为dm 的小段,对每个d m 有d J = R 2对整个环有I = ⎰ R 2d m = mR 2例3质量m ,半径 R 的薄圆盘,求I 。
解:把盘分成无限多个环。
取其中的一个环(半径r ,宽d r ,质量 d m ),d mR•R• m其转动惯量 d I = r 2d m22mdm rdr Rππ=整个盘的转动惯量22322200002122R R RRm m I dI r dm r rdr r dr mR R R ππ=====⎰⎰⎰⎰例4 长为L 、质量为m 的细长直杆,转轴垂直于细杆且通过杆中心 解:杆长为L,质量为m, 则密度为 ρ=m / L 。
刚体定轴转动的动能定理

1
一
转动动能
刚体绕定轴转动时的动能,称为转动动能.
n 1 1 1 2 2 2 2 Ek mi ri ( mi ri ) J 2 2 i 1 2 i 1 2 n
刚体绕定轴转动时的转动动能等于刚体的转动惯量 与角速度平方乘积的一半.
第3章 刚体力学基础
4
例3.5 如图所示,一根质量为m,长为l的均匀细棒 OA,可绕固定点O在竖直平面内转动.今使棒从水平 位置开始自由下摆,求棒摆到与水平位置成30°角时 中心点C和端点A的速度. 解:棒受力如图
6 0
l 1 1 1 2 2 mg cos d J J 0 J 2 2 2 2 2
第3章 刚体力学基础
3–3 刚体定轴转动的动能定理
7
例 一根长为l、质量为m 的均匀细棒, 棒的一端可绕通过 O点并垂直于纸面的轴转动, 棒 的另一端有质量为 m 的小球. 开 始时, 棒静止地处于水平位置A. 当棒转过 角到达位置 B, 棒的 角速度为多少?
oቤተ መጻሕፍቲ ባይዱ
m, l
mg
A
m
B
mg
解: 取小球、细棒和地球为系统, 在棒转动过程中机 械能守恒, 设 A 位置为重力势能零点.
EkA EpA EkB EpB
第3章 刚体力学基础
3–3 刚体定轴转动的动能定理
8
EkA EpA EkB EpB
EkA EPA 0
o
m, l
A
m
1 2 EkB J J J1 J 2 B 2 mg 1 2 4 2 2 J ml ml ml mg 3 3 l 3 EpB (mg sin mgl sin ) mgl sin 2 2 3 g sin 1 2 3 2 2 3 ( ) 0 ml mgl sin 2 l 4 2
高二物理竞赛刚体转动动能定理PPT(课件)

m3g
m1 a1
m1g
a2
T1 T2
讨论:当 m3
T2
T2
m2
a1
T1
a22am1m1m1ma1(22mgm1m2(2mmm12121121m2)gmm1mmm3232)3gg
m2mm12Tg12mm22g2mm1m1 2 gm2
0时
1 2
m2m3
1 2
m3
g
复习
一. 力矩
M rF
律。
已知:M0 I M1= –a |t=0=
求:(t)=?
0
解: 1)以刚体为研究对象;
M+
2)分析受力矩;
M0 I M1
3)建立轴的正方向; 4)列方程:
M0 M1 I
解:4)列方程:
M0 M1 I M0 M1 M0 a
M+ M0
M1=–a
d M0I a
dt
I
I
1 (ln M0 a ) t
分离变量:
a
M0
I
d dt M0 a I
0
d M0 a
t dt
0 I
M0
a
at
eI
M0
1 a
M0(1
at
eI
)
r 质量分别为m1,m2的物体通过轻绳挂在质量为
m3半径为 的圆盘形滑轮上。求物体m1 m2运动
的加速度以及绳子张力
T1.T2 ,(绳子质
量不计) 抵消 已知:m .m .m .r 解(二):考虑杆从水平静止转到铅直方向的过程,重力做功,角速度从 0 -
建立轴的正向:(以逆时针转动方向为正方向) 1)以刚体为研究对象;
0则 0
刚体的能量定轴转动的动能定理
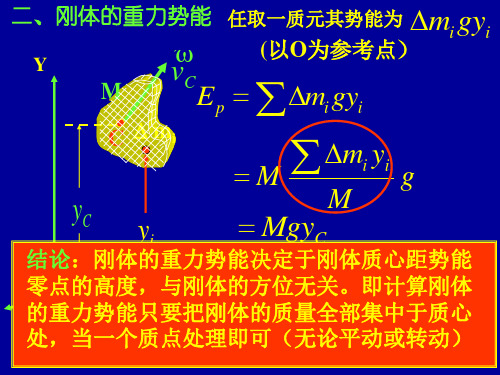
三、转动动能
刚体绕定轴以角速度旋转 刚体的动能应为各质元动能之 和为此将刚体分割成很多很小的
r i vi mi
M
质元 m1, m2 mi mn
r 任取一质元 mi 距转轴 i ,则该质元动能:
mivi2 / 2 mi (ri)2 / 2 miri22 / 2
故刚体的转动动能:
n
Ek Ek
在一微小过程中 力矩作的功
dA Md (1)
在一微小过程中
XX 力1矩O1作的2功2 M M
dA Md (1)
在考虑一个有限过程,设
在力矩作用下,刚体的角
位置由 功
1
2
则力矩的
A dA 2 Md (2) 1
力矩的功反映力矩对空间的积累作用,力矩越 大,在空间转过的角度越大,作的功就越大。 这种力矩对空间的积累作用的规律是什么呢?
/2 mg L cosd
0
2
mgL / 2
N
YZ
XO
r
mg
依动能定理
A力矩
1 2
J2
1 2
J02
A力矩
mg
L 2
mg
L 2
1 2
J
2
0
mgL J
mgL 1 mL2
3g L
3
XX
1
1 O
2
2
2 1
Md
1 2
J
2 2
1 2
J12
M
M
例)设一细杆的质量为m,长为L,一端支以
枢轴而能自由旋转,设此杆自水平静止释放。
求: 当杆过铅直位置时的角速度:
N
YZ
XO
r
mg
2016d2刚体定轴转动的动能定理(理一)
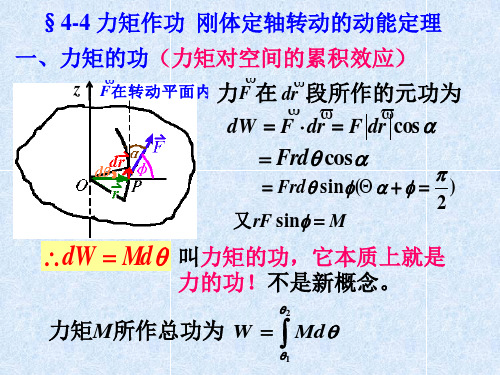
1 2 E k J 2
(相当于平动动能 公式m→J,v→)
四、刚体定轴转动的动能定理
W外
2
d M 外 d J d Jd dt
M
1
外
d
M外
d J J dt
W外
2
J d
1
对定轴刚体,J一定,有
1 1 2 2 W外 J 2 J1 Ek ——动能定理 2 2
dW Md 叫力矩的功,它本质上就是
力的功!不是新概念。
2 1
力矩M所作总功为 W Md
若几个力同时作用,可先求合力矩,再求合 力矩的功 W M 合 d
2
1
可以证明(过程不要求):对刚体, 内力矩不作功。 ∴对刚体, 二、力矩的功率
dW d P M M dt dt
1 2 J mL 3
3g cos 2L
mg
应用动能定理求
1 2 M 外d J 0 2 0
0
L
mg
L 1 1 mg cos d ( mL2 ) 2 2 2 3
3g sin L
1 2 L mg sin J 此题由机械能守恒求解更好: 2 2
M F
0, Fi y 0
Fi 0
iz
0 (对任意z轴)
其中, Fi 0 通常写成分量形式:
ix
例10.长l、重W的均匀梯子,靠墙放置,如图。梯 子下端连一倔强系数为k的弹簧。当梯子靠墙竖直 放置时,弹簧处于自然长度。墙和地面均光滑。 当梯子依墙而与地面成角且处于平衡状态时,
30
解:对(子弹+杆)系统,子弹射入瞬间, 对O轴,M外=0,故角动量守恒,则
3.6 转动动能及转动动能定理

转动动能及转动动能定理
质点转动动能及刚体定轴转动动能
22
1i i i k m E v ∆=∑22221)(21ωωJ r m i i i =∆=∑质点转动动能: 刚体定轴 转动动能: ⎰=21d θθθM W θωθθd d d ⎰=21t
J ⎰=21ωωωωd J 合外力矩对绕定轴转动的刚体所作
的功等于刚体转动动能的增加量。
21222
121d 21ωωθθθJ J M W -==⎰
已知:一长为l , 质量为m 的均匀细杆,用摩擦可忽略的柱铰链悬挂于A 处,欲使静止的杆AB自竖直位置恰好能转至水平位置,
求:必须给杆的最小初角速度。
解:设必须给杆的最小初角速度为 则杆的初动能为: 2
121ωJ E k =达到水平位置杆的末动能为: 0
1=k E 初末过程中重力矩做的功为: 2
l
mg W -=2
21
02ωJ l
mg -=-23
1ml J =l
g 30=ω⇒0
ω
已知:一质量为 ,半径为 R 的圆盘,可绕一垂直通过盘心的 无摩擦的水平轴转动。
圆盘上绕有轻绳,一端挂质量为 m 的物体。
问:物体在静止下落高度 h 时,
其速度的大小为多少?
设绳的质量忽略不计。
'm
22211mgh mv J 22v
1
,J m R r 22mgh
v m m 2
ωω=+'==='
+解:
Thanks!。
刚体力学_功 动能定理
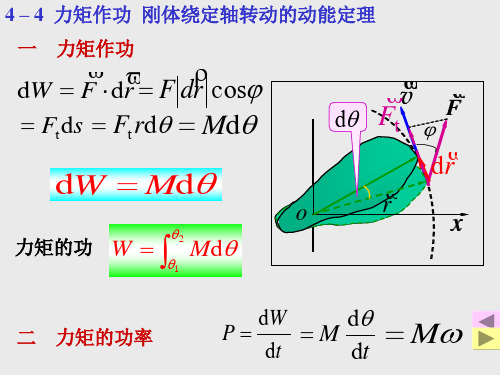
m
.
N
R
m1
m2 解: 把m1、m2和m看作一系统 系统所受 m g 看作一系统,系统所受 看作一系统 1 m2 g 合外力有重力m 、 合外力有重力 1g、m2g,这两个力对轴 这两个力对轴 支撑力N通过转轴 的力矩分别为m 的力矩分别为 1gR、m2gR;支撑力 通过转轴 对轴的力 、 支撑力 通过转轴,对轴的力 矩为零.加上阻力矩 加上阻力矩M 系统所受合外力矩为 顺时针为正) 系统所受合外力矩为(顺时针为正 矩为零 加上阻力矩 f ,系统所受合外力矩为 顺时针为正 M=m2gR-m1gR-Mf 系统的总角动量为(顺时针为正 顺时针为正) 系统的角 m: Jω 系统的总角动量为 顺时针为正 动量包括 m1: Rm1v L=Jω+Rm1v+Rm2v m2: Rm2v
1 1 1 2 2 2 mv 0 = mv + Jω 2 2 2
的圆盘, 例 一质量为 m' 、半径为 R 的圆盘,可绕一垂 圆盘上绕有轻绳, 直通过盘心的无摩擦的水平轴转动 . 圆盘上绕有轻绳, 问物体由静止下落高度 一端挂质量为m 一端挂质量为 的物体 . 问物体由静止下落高度 h 时, 其速度的大小为多少? 其速度的大小为多少 设绳的质量忽略不计 . v 对圆盘做功, 解1 拉力 FT 对圆盘做功,由刚体绕定轴转动的动 v 能定理可得, 能定理可得,拉力 FT 的力矩所作的功为
o
圆 锥 摆
o
v θ T
'
m
v v
v p
o
v v
R
以子弹和杆为系统 守恒; 动量不守恒; 守恒; 角动量 守恒; 机械能 不守恒 .
圆锥摆系统 守恒; 动量不守恒; 对 O'O 轴角动量 守恒; 守恒; 机械能 守恒 .
动能定理与刚体的转动

动能定理与刚体的转动为了深入了解动能定理与刚体的转动,我们首先需要了解它们的基本概念和原理。
在本文中,我们将介绍动能定理的定义及应用,并详细探讨刚体的转动,包括刚体的转动惯量、角动量和动能。
一、动能定理动能定理是力学中重要的定理之一,它描述了物体动能的变化与物体所受的合外力之间的关系。
动能定理可以表述为:物体的动能变化等于物体所受的合外力对它所做的功。
动能定理的数学表达式为:\[ \Delta KE = W_{\text{net}} \]其中,\[ \Delta KE \] 表示物体动能的变化,\[ W_{\text{net}} \] 表示合外力所做的功。
动能定理适用于各种形式的力学系统,包括质点、刚体等。
通过动能定理,我们可以确定物体在受到力的作用下的运动状态,并推导出与力、速度、质量等相关的物理量。
二、刚体的转动刚体是指形状保持不变的物体,其转动是指固定点周围的旋转运动。
刚体的转动有着独特的性质和规律,其中包括转动惯量、角动量和动能。
1. 转动惯量转动惯量是刚体转动惯性的度量,它表示刚体对于绕特定轴线转动的惯性大小。
转动惯量的数学表达式为:\[ I = \int r^2 dm \]其中,\[ I \] 表示转动惯量,\[ r \] 表示离轴距离,\[ dm \] 表示质量元素。
转动惯量的大小取决于刚体的形状和质量分布,不同的轴线对应着不同的转动惯量。
2. 角动量角动量是描述物体旋转状态的物理量,它表示物体绕某一轴线旋转时的运动状态。
角动量的定义为:\[ L = I \cdot \omega \]其中,\[ L \] 表示角动量,\[ I \] 表示转动惯量,\[ \omega \] 表示角速度。
角动量是与物体的转动状态密切相关的物理量,它与转动惯量和角速度的乘积成正比。
3. 动能刚体的转动动能由两部分组成,分别是平动动能和转动动能。
平动动能表示刚体的质心的运动状态,转动动能表示刚体绕轴线的旋转状态。
05-3刚体绕定轴转动的动能定理

2
物体下滑的速率 是物体在斜面上 位置的函数
2)物体在斜面上能滑多远 ) 物体的速率
R
m
2
2mgx sin θ − kx v= 2 m+ J /R
2
m
θ
x
k
当v= 0 时物体在斜面上停止下滑
2mgx sin θ − kx = 0
2mg sin θ x= k
1 2 2 = (∑ mi ri )ω 2
z
1 2 2 Ek = (∑ mi ri )ω 2 i =1
刚体对定轴 的转动惯量
n
ω
vi
mi
J = ∑ mi ri
i =1
n
2
v o ri
1 2 Ek = Jω 2
对比质点 的动能
——刚体的转动动能 刚体的转动动能
1 2 Ek = mv 2
v dr
v F
当力作用在质点上使它在力的方向发 生位移, 生位移,该力就对质点做功
v v dW = F ⋅ dr
z
刚体绕固定轴转动时, 刚体绕固定轴转动时,外力使刚体上 的质点都作圆周运动, 的质点都作圆周运动,外力也在做功 外力对刚体做功要用力矩和角位移 的乘积形式来表示, 的乘积形式来表示,称为力矩的功
ω
vi
4-4 刚体绕定轴转动的动能定理 -
力矩是改变刚体转动状态的原因
刚体定轴 转动定律
M = Jα
——力矩的瞬时作用效应 力矩的瞬时作用效应 还应该研究力矩的累积效应—— 还应该研究力矩的累积效应 力矩对时间累积效应 刚体的角动量定理 力矩对空间的累积 刚体定轴转动的动能定理 如何表示刚体的转动动能呢? 如何表示刚体的转动动能呢? 高速转动的砂轮具有 转动动能, 转动动能,它能通过 摩擦转化为热能
3-3刚体转动的动能定理

T2
( m1
1 2
M )m 2 g
1 2
m1 m 2
M
以上两种方法,都是求解这类问题的基本方法, 都 应该理解和掌握。
例4:一个转动惯量为2.5 kgm2 、直径为60cm 的飞轮,正以130 rads1 的角速度旋转。现用闸瓦 将其制动, 如果闸瓦对飞轮的正压力为 500 N,闸瓦 与飞轮之间的摩擦系数为0.50。求:
设刚体有n个质点组成,其中第i个质点的质 量 为 mi ,它到转轴的距离为 ri,速度大小为vi ,则该质 1 1 E m vБайду номын сангаас,因 vi ri w ,所以 E m r w 。因 点的动能 2 2 此,整个刚体的动能为
2 ki i i
2
2
ki
i i
1 1 n 2 2 Ek mi vi mi ri w2 2 i 1 i 1 2
m2
m1
解:物体m1、m2和滑轮的受力情况如图所示。 列方程
T1 =m1 a
( 1)
FN
m2 g T2 = m2 a (2)
对于滑轮
T1 T1 T2 T2
α
1 2 T2 r T1r I M r 2
辅助方程
( 3)
m1 g
a
( 4)
m2 g
r = a
n
式中 i 1 是刚体的转动惯量I,所以绕定轴转 动的动能可以写为
mi vi
n
2
1 2 E k Iw 2
三、定轴转动的动能定理
设刚体在 合 外力矩M的作用下,绕定轴转过角位 移 d ,合外力矩对刚体作的元功为
dA Md
刚体的能量定轴转动的动能定理

/2 mg L cosd
0
2
mgL / 2
N
YZ
XO
r
mg
依动能定理
A力矩
1 2
J2
1 2
J02
A力矩
mg
L 2
mg
L 2
1 2
J
2
0
mgL J
mgL
1 mL2
3g L
3
三、转动动能
刚体绕定轴以角速度旋转 刚体的动能应为各质元动能之 和为此将刚体分割成很多很小的
r i vi mi
M
质元 m1, m2 mi mn
r 任取一质元 mi 距转轴 i ,则该质元动能:
mivi2 / 2 mi (ri)2 / 2 miri22 / 2
故刚体的转动动能:
n
Ek Ek
力 F 作的功:
ds rd
dA F ds F sin rd Md
在一微小过程中 力矩作的功
dA Md (1)
在一微小过程中
XX 力1矩O1作的2功2 M M
dA Md (1)
在考虑一个有限过程,设
在力矩作用下,刚体的角
位置由 功
1
2
则力矩的
A dA 2 Md (2) 1
力矩的功反映力矩对空间的积累作用,力矩越 大,在空间转过的角度越大,作的功就越大。 这种力矩对空间的积累作用的规律是什么呢?
XX
1
1 O
2
2
2 1
Md
1 2
J
2 2
1 2
J12
M
M
例)设一细杆的质量为m,长为L,一端支以
枢轴而能自由旋转,设此杆自水平静止释放。
刚体力学第2讲——定轴转动中的功能关系刚体的角动量定理和角动量守恒定律

动相反方向作圆周运动(如图) 求:1) 圆盘对地的角速度.
2)欲使圆盘对地静止,人应沿着圆周对圆盘的速 度的大小及方向?
R
R/2 v
解:取人和盘为系统,
M 外 0 系统的角动量守恒.
R /2
Ro
v
(1)开始系统的角动量为
m
12 R
2
0
1 2
M
R 20
后来:
m
1 4
R 2 mE
1 2
M
R 2 ME
mE ME mM 21 M R 20 / 40
R /2
Ro
v
MR 40
2
ME
2v R
M
R 2 ME
/2
为
亦即l>6s;当‘’取负值,则棒向右摆,其条件为
3gl 3 2gs 0 亦即l<6s
棒的质心C上升的最大高度,与第一阶段情况相似,也可由 机械能守恒定律求得:
mgh 1 1 ml 2 2
23
把式(5)代入上式,所求结果为
h l 3s 6sl
解 这个问题可分为三个
阶段进行分析。第一阶段 是棒自由摆落的过程。这
O
时除重力外,其余内力与
外力都不作功,所以机械
能守恒。我们把棒在竖直
C
位置时质心所在处取为势
能零点,用表示棒这时
的角速度,则
mg l 1 J 2=1 1 ml 2 2
22
23
(1)
刚体的动能定理

质点系动能 平动刚体动能 定轴转动刚体动能 平面运动刚体动能
质点系的动能
质点系∶有n个质点 第i个质点为Mi ,质量为mi ,速度为vi , 动能为
1 2 质点系的动能以T表示 m i vi
2
T
1 2
mv
2
刚体与质点系的关系
刚体∶实际工作中常见的质点系。 刚体动能的表达式∶ 与刚体的运动形式有关。 刚体运动形式不同,刚体动能 的表达式不一样。
1 2
J C '
2
2
1 2
( J C Md )
2
2 2
2
J C
1 2
Md
2
质心运动的速度.
T
1 2
Mv C
1 2
J C
2
刚体平面运动的动能 等于其随同质心运动的动能与 绕过质心的轴转动的动能之和。
平动刚体的动能
刚体平动∶各点的速度都相同。 应用质点系的动能表达式∶
T 1 2
2
Mv
2
1
mv
2
1 2
v
2
m
平动刚体的动能等于 其质心的动能
定轴转动刚体的动能
刚体定轴转动,各点的角速度都相同。
T 1 2 1 2
2 mv
2
1
1
22源自2mr 22
m r 定轴转动刚体的动能
等于刚体对转轴的转 动惯量与角速度平方 乘积的一半
2
J z
平面运动刚体的动能
刚体的平面运动=刚体绕速度瞬心的转动。 设速度瞬心为C‘,动能可写成∶
T
1 2
J C ' ....( 1)
03-1刚体定轴转动的动能定理和转动定律 (2)

定轴转动
非定轴转动
刚体的自由运动:
既平动又转动:质心的平动加绕质心的转动
刚体的一般运动 质心的平动
+
绕质心的转动
二.刚体定轴转动的运动学
角位置
(t )
>0 <0
0
z
(t )
p
{
逆时针转动 顺时针转动
x
转动平面
参考轴
d 角速度 dt
方向:右手螺旋定则
1 1 2 2 F R d R F d J J 0 0 T 0 T 2 2 1 1 1 1 2 2 2 mgh mv mv0 ( J J 02 ) 2 2 2 2
FN
FT FT
o P'
FT
m
FT
物体由静止开始下落
拉力 FT 对圆盘做功,由刚体绕定轴转 动的动能定理可得
1 1 2 2 mgh R FT d mv mv0 0 2 2
FT
0
FT Rd R FT d
0
P
m
R
o
m' h m
FN
FT
m
1 2 1 2 J J 0 2 2
o P'
1 E k J 2 2
刚体 转动 动能
1 2 平动动能 Ek mv 2 比较: 1 转动动能 Ek J 2 2
d d d d d d dd J J J J J J M JJ 4 定轴转动的动能定理 d d dt d dt d dt dt 2 2 2 2 1 11 2 2 1 2 2 Md J d J J W Md J d J J 2 12 1 1 2 1 1 1 22 2
2.3 刚体的转动动能

信息学院 物理教研室
由于静止下落,则初始各动能为零: 由于静止下落,则初始各动能为零:
1 11 1 1 2 2 2 2 ⇒ mgh = mv + Jω = mv + m ′R ω 2 2 2 2 2 2 1 1 2 = mv + m ′v 2 2 4
⇒v= 4mgh m ′ + 2m
一、刚体的转动动能 刚体可看作是由许多的质点组成, 刚体可看作是由许多的质点组成,刚体的转 动动能是刚体各部分动能的总和。 动动能是刚体各部分动能的总和。
1 E k = ∑ ∆m i ri2ω 2 2 1 = ∑ ∆m i ri2 ω 2 2 1 2 = Jω 2
(
)
注意: 为瞬时角速度, 注意 ω为瞬时角速度, Ek是刚体的瞬时转动 动能。 动能。
信息学院 物理教研室 x
dm
mg
dmg
由刚体转动动能定理得: 由刚体转动动能定理得
1 1 2 2 W = ∫ Mdθ = Jω − Jω 0 2 2
所以, 所以,有:
∫
θ
0
1 1 mgl cos θ d θ = J ω 2 2
2
1 1 ⇒ mgl sin θ = J ω 2 2 2
⇒ω =
mgl sin θ = J
∫
dmg
信息学院 物理教研室
根据质心定义有: 根据质心定义有 ∫ xdm= mx c ⇒ M = mgx c = xc 重力对整个棒的合力 矩与全部重力集中作用在 O θ 质心所产生的力矩一样。 质心所产生的力矩一样。 C 1 1 x c = l cos θ ⇒ M = mgl cos θ 2 2 1 mgl cos θ M 3 g cos θ 2 则: α = = = 1 J 2l 2 ml 3
刚体定轴转动的动能定理

FTh
1 2
m2v 2
由刚体动能定理
m2
h
FT R
1 2
I 2
1 4
m1R2 2
上页 下页 返回 结束
约束关系
R h
第七章 刚体力学
v R
联立得
v 2 m2 gh m1 2m2
方法2. 利用质点系动能定理求解
将转动柱体、下落物体视作质点系
由质点系动能定理
m2 gh
1 2
m2v 2
1 2
I
2
第七章 刚体力学
§7.4刚体定轴转动的动能定理
§7.4.1力矩的功 §7.4.2 刚体定轴转动的动能定理 §7.4.3 刚体的重力势能
上页 下页 返回 结束
第七章 刚体力学
§7.4.1力矩的功
刚体中P点在力 F
的作用下位移
dr
则力元功
dA F dr F rd
rd 0
杆处于铅直位置时不受力矩作用,由转动定理,角
加速度为零,所以 FNt 0
又
rc
1 2
l,
vc
v 2
1 2
3gl
FN
FNn
mg
3 2
mg
5 2
mg
方向向上 .
上页 下页 返回 结束
Eki
1 2
mi vi2
刚体的动能
Ek
Eki 12mivi 2
1 2mi
ri
2
2
1 2
(
mi ri 2 ) 2
Ek
1 2
Iz 2
上页 下页 返回 结束
第七章 刚体力学
2. 定轴转动刚体的动能定理
M z I z
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§ 3.2 刚体转动的动能定理
一、力矩的功 1 力矩的定义
若作用的质点上的力为F ,则将r ×F 定义为力F 对O 点的力矩,记为M 。
M r F =⨯
M 、F 、r 三者的方向构成右手螺旋关系。
大小:
方向:右手法则
2 力矩的功
设:;转盘上的微小质量元Δm 在力F 作用下以R 为半径绕O 轴转动,在dt 时间内转过角度d θ, 对应位移d r,路程ds,此时F 所做的元功为
则总功为
二、转动惯量
设初速为零,质量元Δm 的动能为
转盘的总动能
1 定义:
为物体的转动惯量。
F
t
F n
F t
F d r
t t d d d d A F r F s F r θ
=⋅==d d A M θ=2
1
d A M θθθ
=⎰α
r
sin t M Fr F r
α==t
F d r
12
ki i i
E m v =21
2
k ki i i i i E E m ==∆∑∑v 22
1()2i i i m r ω=∆∑2i i i
I m r =∆∑
意义:由质量和质量对于转轴的分布情况决定。
描述转动的惯性。
例:一头粗,一头细的杆以不同端作轴转动是,其转动惯量不同。
单位:SI 制 kg m 2
2 定轴转动物体转动惯量的计算 质量不连续分布的质点系:转动惯量定义为各个质点对该定轴的转动惯量之和
2i i i
I m r =∑
质量连续分布的刚体:转动惯量定义为各个质点对该定轴的转动惯量的积分。
2m
I r dm =⎰
转动惯量的大小不仅取决于物体的质量,还与质量的分布和轴线的位置有关。
例1 求小球m 的转动惯量。
解:m 看作质点 I = m R 2
例2 质量为m 的细圆环,求I 。
解:把环分成无限多个质量为dm 的小段,对每个d m 有
d J = R 2
对整个环有
I = ⎰ R 2d m = mR 2
例3质量m ,半径 R 的薄圆盘,求I 。
解:把盘分成无限多个环。
取其中的一个环(半径r ,宽d r ,质量 d m ),
d m
R
•
R
• m
其转动惯量 d I = r 2d m
2
2m
dm rdr R
ππ=
整个盘的转动惯量
2
2
3222000
021
22R R R
R
m m I dI r dm r rdr r dr mR R R ππ=====⎰⎰⎰⎰
例4 长为L 、质量为m 的细长直杆,转轴垂直于细杆且通过杆中心 解:杆长为L,质量为m, 则密度为 ρ=m / L 。
以杆中心O 点为转轴,在距o 点为r 处取微小质量元dm =ρdr, 杆的转动惯量为
例5 转轴垂直于细杆且通过杆的一端 以杆中心O /点为转轴,同上
2
22
2
22
322
13l l l
l l
l
I r dm r dr r ρρ---=
=
=⎰⎰
2
112
I mL
=
2
1
3
I mL
=
2020
313
l
l
l
o I r dm
r dr
r
ρρ===⎰⎰
3 几种典型的匀质刚体的转动惯量
4 影响转动惯量的三个因素
(1)刚体自身的性质如质量、大小和形状;
(2)质量的分布; (质量分布越靠近边缘转动惯量越大) (3)转轴的位置。
(同一个刚体对不同的轴转动惯量不同) 5 平行轴定理和转动惯量的可加性 1) 平行轴定理
设刚体相对于通过质心轴线的转动惯量为Ic ,相对于与之平行的另一轴的转动惯量为I ,则可以证明I 与Ic 之间有下列关系 2c I I md =+ 2)转动惯量的可加性
对同一转轴而言,物体各部分转动惯量之和 等于整个物体的转动惯量。
例6质量m ,长为l 的均匀细棒,求对于通过质心的垂直轴的转动惯量Jc 和通
2
c I I m
d =+
过端点a 的垂直轴的转动惯量J.
解:建立如图坐标Ox
2
2222
2
2
112
l l c l l m J x dm x dx ml l
++
--
=
=
=
⎰
⎰
由平行轴定理有
2
2211
1223a l J ml m ml ⎛⎫=+= ⎪⎝⎭
2
c 1
2I mR =2c 12
I mR =
如果刚体偏心转动,转轴通过半径的中点且垂直于盘面。
求盘对此轴的转动惯量I 。
解:题给两平行轴之间的距离
1
2
d R =
2
c I I m
d =+得刚体绕偏心轴的转动惯量
22213
()224
R I mR m mR =
+=由平行轴定理
例 3-2 如图所示,一圆盘状刚体的半径为 R ,质量为 m ,且均匀分布。
它对过质心并且垂直于盘面的转轴的转动惯量用Ic 表示。
例3-3 如图所示,某装置由均质细杆和均质圆盘构成。
杆的质量为 ,长 L 。
杆对O 轴的转动惯量 2
111
3
I m L =1
m
圆盘质量是 ,半径为R 。
,得知它对过质心C 且垂直于盘面的转轴的转动惯量为 2m
22c 21
2
I m R =
求此装置对轴O 的转动惯量I 。
x
三、刚体绕定轴转动的动能定理 1 刚体绕定轴转动的转动动能
2 动能定理
合外力矩对绕定轴转动的刚体所作的功等于刚体转动动能的增量。
刚体作为一个特殊的质点系,此质点系的动能定理为
21
e k k A E E =-2
1
2 2
2 111d θωω22
θM I I =
-⎰ θ
刚体定轴转动的动能定理
解:已知杆对轴O 的转动惯量
盘对轴C 的转动惯量
22c 21
2
I m R =
由平行轴定理得盘对轴O 的转动惯量
22c 2(I I m R L =++2221
(2
m R m R L =
++由转动惯量的可加性,得整个装置对轴 O 222
1212211
()32
I I I m L m R m R L =+=+++2111
3
I m L =
222
2k 111222
i i i i i i E m v m r I ωω
===∑∑ 由于刚体的大小、形状不变,其上任何两质点间没有相对位移。
即:
i 0
A =。
