线性系统的状态空间描述
线性系统的状态空间描述

第一章 线性系统的状态空间描述 1. 内容系统的状态空间描述化输入-输出描述为状态空间描述 由状态空间描述导出传递函数矩阵 线性系统的坐标转换组合系统的状态空间方程与传递函数矩阵2. 基本概念系统的状态和状态变量状态:完全描述系统时域行为的一个最小变量组。
状态变量:构成系统状态的变量。
状态向量设系统状态变量为)(,),(),(21t x t x t x n 写成向量形式称为状态向量,记为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)()()()(21t x t x t x t x n状态空间状态空间:以状态变量为坐标轴构成的n 维空间。
状态轨迹:状态变量随时间推移而变化,在状态空间中形成的一条轨迹。
3. 状态空间表达式设系统r 个输入变量:)(,),(),(21t u t u t u r m 个输出:)(,),(),(21t y t y t y m n 个状态变量:)(,),(),(21t x t x t x n例:图示RLC 电路,建立状态空间描述。
电容C 和电感L 两个独立储能元件,有两个状态变量,如图中所注,方程为)()()()()()(t i dtt du C t u t u t Ri dtt di LL c c L L ==++ )()(),()(21t u t x t i t x c L ==状态方程)(01)()(0/1/1/)()()()()()()()(212112211t u t x t x C L L R t xt x t x t xC t u t x t Rx t x L ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡⇔⎩⎨⎧==++⇔输出方程[]⎥⎦⎤⎢⎣⎡==)()(01)()(21t x t x t u t y c 一般定义状态方程:状态变量与输入变量之间的关系[][][]t t u t u t u t x t x t x f t xdt t dx t t u t u t u t x t x t x f t xdt t dx t t u t u t u t x t x t x f t xdt t dx r n n n n r n r n );(,),(),();(,),(),()()();(,),(),();(,),(),()()();(,),(),();(,),(),()()(212121212222121111======用向量表示,得到一阶的向量微分方程[]t t u t x f t x),(),()(= 其中n n r r n n f f f f t u t u t u t u t x t x t x t x R R R ∈⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∙∙∙=∙∈⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=∈⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)()()(:)(,)()()(:)(,)()()(:)(212121输出方程:系统输出变量与状态变量、输入变量之间的关系,即[][][]t t u t u t u t x t x t x g t y t t u t u t u t x t x t x g t y t t u t u t u t x t x t x g t y r n m m r n r n );(,),(),();(,),(),()();(,),(),();(,),(),()();(,),(),();(,),(),()(2121212122212111=== 用向量表示为[]t t u t x g t y ),(),()(=4系统分类:1) 非线性时变系统[][]⎩⎨⎧==t t u t x g t y t t u t x f t x ),(),()(),(),()(2) 非线性定常系统[][]⎩⎨⎧==)(),()()(),()(t u t x g t y t u t x f t x3) 线性时变系统⎪⎩⎪⎨⎧+++++=+++++=rnr n n nn n n r r n n u t b u t b x t a x t a xu t b u t b x t a x t a x)()()()()()()()(1111111111111写成向量形式即为⎩⎨⎧+=+=)()()()()()()()()()(t u t D t x t C t y t u t B t x t A t x其中:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)()()()()()()()()()(,)()()()()()()()()()(212222111211212222111211t b t b t b t b t b t b t b t b t b t B t a t a t a t a t a t a t a t a t a t A nr n n r r nn n n n n ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)()()()()()()()()()(,)()()()()()()()()()(212222111211212222111211t d t d t d t d t d t d t d t d t d t D t c t c t c t c t c t c t c t c t c t C mr m m r r mn m m n n4) 线性定常系统⎩⎨⎧+=+=)()()()()()(t Du t Cx t y t Bu t Ax t x5 状态空间表达式的系统结构图状态和输出方程可以用结构图表示,形象地表明系统中信号传递关系。
第22 线性系统的状态空间描述
其中 A(t) n×n — 系统矩阵 B(t) n×r — 输入矩阵 C(t) m×n — 输出矩阵 D(t) m×r — 前馈矩阵
D(t)
X
X
U
B(t)
C(t)
Y
A(t)
离散时间线性系统的状态空间描述
离散系统:各变量在离散时刻取值,状态空间反映离 散时刻的变量组间的因果关系和变换关系。用 k=0,1,2…表示离散时刻。 状态空间描述形式:
的因果关系,即输入和输出间的因果关系。 例如:线性定常、单输入-单输出系统,外部描述为线性常系
数微分方程。
y(t) an1 y(n1) (t) a1 y(t) a0 y(t) bm u(m) (t) bn1u(m1) (t ) b1u(t ) b0u(t )
零初始条件下,传递函数为:
输出方程/量测方程:代数方程
y1 g1 ( x1, , xn ; u1, , ur ; t)
t t0
ym gm ( x1, , xn ; u1, , ur ; t)
向量形式:
y g(x, u, t)
• 线性系统的状态空间描述
x A(t)x B(t)u
y
C(t)
x
D(t
)u
t t0
L diL dt
L diL dt
0 e
e(t)
R1
C
iC
L
iL U c R2 U R2
uc
iL
(R1
1
R2 R1
)C
L(R1 R2 )
(
R1
R1 R2 R1R2
)C
uc
iL
(
R1
1
R2 R2
)C
e
线性系统理论 第2章 线性系统的状态空间描述
u(k )
H (k )
x(k 1)
x(k )
单位延迟
C (k )
y(k )
G (k )
7/7,11/50
2.3.连续变量动态系统按状态空间描述的分类
线性系统和非线性系统
设系统的状态空间描述为 x f ( x, u, t ) y g ( x, u, t )
向量函数
g1 ( x, u, t ) f1 ( x, u, t ) g ( x, u , t ) f ( x, u , t ) ,g ( x, u, t ) 2 f ( x, u , t ) 2 g q ( x, u , t ) f n ( x, u , t )
和t≥t0 各时刻的任意输入变量组 u1 (t ),u2 t ,, u p (t ) 那么系统的任何一个内部变量在t≥t0各时刻的运动行为也就随之而完全确定
3/4,3/50
(2).状态变量组最小性的物理特征: 少一个不行,多一个没用 (3). 状态变量组最小性的数学特征:极大线性无关变量组 (4). 状态变量组的不唯一性 :任意
1/18,14/50
结论1
给定单输入,单输出线性时不变系统的输入输出描述,
y ( n) an1 y ( n1) a1 y (1) a0 y bmu ( m) bm1u ( m1) b1u (1) b0u
Y (s) bm s m bm1 s m1 b1 s1 b0 g ( s) U ( s) s n an1 s n1 a1 s a0
时变系统和时不变系统
f f ( x, u ) 若向量f,g不显含时间变量t,即 g g ( x, u )
现代控制工程-第二章线性系统的状态空间描述

1 x3 s
1 s
1 x1 s
y(t )
2
3
8 64
解:第一步:化简方框图,使得整个系统只有标准积分器(1/s)、 比例器(k)及加法器组成。 第二步:将上述调整过的结构图中的每个标准积分器(1/s) 的输出作为一个独立的状态变量xi,积分器的输入端就是状态变 量的一阶导数dxi/dt。 第三步:写出每个状态变量的一阶微分方程,从而写出系统 的状态方程。
y Cx Du
图2-2 系统动态方程的方块图结构
状态空间分析法具有下列优越之处:
便于在数字计算机上求解;
容易考虑初始条件; 能了解并利用处于系统内部的状态信息; 数学描述简化;
适于描述多输入-多输出、时变、非线性、随机、离散等各类 系统,是最优控制、最优估计、辨识、自适应控制等现代控制系 统的基本描述方法。
例2.2.3求如图所示系统的动态方程。
(a)系统方块图
u(t )
s 1 s2
1 s3
1 s 2 8s 64
y(t )
(b)第一次等效变换
1 s3
u(t )
1 s2
1 s( s 8)
y(t )
64
(c)由标准积分器组成的等效方块图
u(t )
1 x4 s
(2-5)
y t cx t du(t )
,cn ,d为直接联系输入量、输出量 其中 c c1,c2, 的前向传递(前馈)系数,又称前馈系数。
多输入-多输出(含q个输出变量)线性定 常连续系统的输出方程一般表达形式为:
y1 c11 x1 c1n xn d11u1 d1 pu p yq cq1 x1 cqn xn d q1u1 d qp u p
第2章 线性系统的状态空间描述

定义2.5 [特征多项式] 特征多项式] 定义
2.4 线性时不变系统的特征结构
特征多项式α(s)的计算方法 的 特征多项式
莱弗勒(Leverrier)递推算法 递推算法 莱弗勒
2.4 线性时不变系统的特征结构
α ( s ) = s n + α n −1s n −1 + L + α1s + α 0
0 1 0 A = 0 0 1 0 −1 −1
5,化下列各状态方程为对角线规范型或约当规范型 化下列各状态方程为对角线规范型或约当规范型
8 −8 −2 2 3 & x = 4 −3 −2 x + 1 5 u 3 −4 1 7 1
0 1 4 & x= x + 2 u −9 −6
作 业
6,计算下列状态空间描述的传递函数 计算下列状态空间描述的传递函数 −5 −1 2 & x= x + 5 u 3 −1 y = [1 2] x + 4u 7,给定反馈系统如下图所示 给定反馈系统如下图所示
& 为 x1 = y , x2 = y ,列出系统的状态方程和输
出方程
u
+ −
&& y
+
∫
by 2
& y
二次部件
∫
y
+ + +
a (t )
k
作 业
2,试求出下列各个输入输出描述的一个状态空间描述 试求出下列各个输入输出描述的一个状态空间描述
&&& + 2&& + 6 y + 3y = 5u y y & &&& + 2&& + 6 y + 3 y = 7u + 5u & y y & & & 3&&& + 6 && + 12 y + 9 y = 6u + 3u y y
第2章 线性系统的状态空间描述

(t
t1
)dt
1
(2)对任何在 t1时刻连续的函数f(t),有
f (t) (t t1)dt f (t1)
12
第2章 线性系统的状态空间描述
➢非零初始条件与等价的脉冲输入 结论:非零初始条件对应的系统响应
等效于在初始时刻脉冲输入时的系统响应。 以后在建立系统的输入—输出描述
时,均假定系统的初始条件为零。
u p1
System
yq1
视系统为 black box
5
第2章 线性系统的状态空间描述
例如:
从输入—输出关系来看,它们具有相同的传递函数:
G(s) 1 s 1
实际上这两个系统是不等价的,一个是能观不能控的, 一个是能控不能观的。
表明:系统的内部特性比起由传递函数表达的外部特性 要复杂得多,输入—输出描述没有包含系统的全部信息, 不能完整的描述一个系统。
或
x(k 1) y(k) g
f [
[ x(k x(k ),
), u(k), k u(k), k ]
]
24
第2章 线性系统的状态空间描述
(4).线性系统状态空间表达式:状态方程与输出方 程都是线性方程的系统是线性系统。线性系统的状态方 程是一阶向量线性微分方程或一阶向量线性差分方程。
1 非零初始条件与脉冲输入
➢ 系统的初始条件为零是指系统在初始时刻没有能 量储备,系统输出只由此后的输入唯一地确定 。
➢ 在建立线性系统的输入—输出描述 时,必须假设系统的初始条件为零。
初始条件不为零 时如何处理?
➢ 初始条件不为零时,可以将非零的初始条件 等效成在初始时刻的一个脉冲输入。
10
第2章 线性系统的状态空间描述
2线性系统的状态空间描述

C m ia J
dt
2
f
转动惯量, 粘性摩擦常数, m 电磁转矩常数,e 电势常数 C C f
令 x1 , x 2 , x 3 i a
x1 x 2 x2 x3 f J Ce La x2 x2 Cm J Ra La x3 x3 u La
结构图
x2
状 态 轨迹
A
( x1 ( t 0 ), x 2 ( t 0 ))( x1源自( t1 ), x 2 ( t1 ))
B
0
x1 ( t ) x (t ) x 2 (t )
t
x1
状态空间分析法举例
例1求图示机械系统的状态空间表达式
外力 u ( t )
K ---弹性系数 m
7.状态空间表达式(动态方程):{A,B,C,D}
x f ( x, u , t) y (t ) g ( x , u , t )
x ( t k 1 ) f ( x , u , t k ) y (tk ) g ( x , u , tk )
f,g-线 性 函 数 线 性 系 统
u
y 1
0
例4. 一长度为l ,质量为m的单倒立摆,用铰 链安装在质量为M的小车上,小车受电机操纵, ,在水平方向施加控制力u,相对参考坐标系 产生位移x。要求建立该系统的状态空间表达 式。
m
x
l
u
M
设小车瞬时位置为 x 摆心瞬时位置为 ( x l s i n ) 在水平方向,由牛顿第二定律
yq
u [u1 , u 2 , , u p ]
T
y [ y1 , y 2 , , y q ]
第二章线性系统的状态空间描述1

第二章 线性系统的状态空间描述§2-1 状态空间的基本概念1、状态:系统的状态,是指系统的过去、现在和将来的状况。
(如:一个质点作直线运动,它的状态就是它每个时刻的位置和速度)2、状态变量:能完全表征系统运行状态的最小数目的一组变量。
(如果用最少的n 个变量x 1(t), x 2(t),……, x n (t)就能完全描述系统的状态,那么这n 个变量就是一组状态变量。
)3、状态向量:设一个系统有n 个状态变量,即x 1(t),x 2(t),……,x n (t),用这n 个状态变量作为分量构成的向量x(t)称为该系统的状态向量。
记为Tn t x t x t x t x )](,),(),([)(21 =4、状态空间:由n 个状态变量作为坐标轴所构成的n 维空间,称为状态空间。
引入了状态和状态空间的概念之后,就可以建立动力学系统的状态空间描述了。
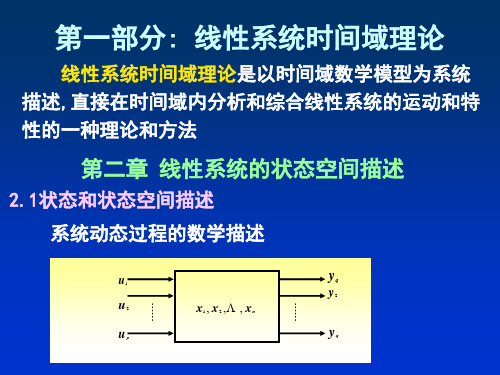
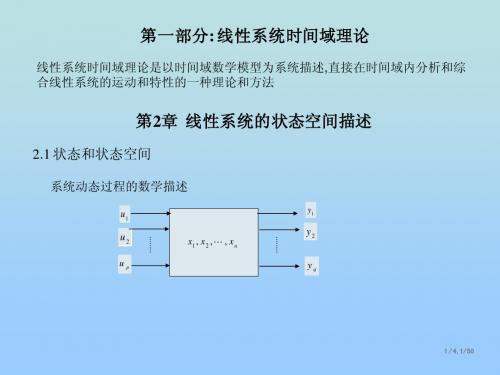
从结构的角度讲,一个动力学系统可用图2-1所示的方块图来表示。
其中x(t)表征系统的状态变量,u(t)为系统控制量(即输入量),y(t)为系统的输出变量。
与输入—输出描述不同,状态空间描述把系统动态过程的描述考虑为一个更为细致的过程:输入引起系统状态的变化,而状态和输入则决定了输出的变化。
5、状态方程:状态变量的一阶导数与状态变量、输入量的关系,称为系统的状态方程。
例:设单输入线性定常系统(LTI-Linear Time Invariant )的状态变量为x 1(t),x 2(t),……,x n (t),输入为u(t),则一般形式的状态方程为:)()()()()()()()()()()()()()()()()()()()()(2211222221212112121111t u b t x t a t x t a t x a t x t u b t x t a t x t a t x a t x t u b t x t a t x t a t x a t x n n nn n n nn n n n ++++='++++='++++='图2-1 动力学系统结构示意图上式可写成向量—矩阵形式:其中:6、输出方程:在指定系统输出的情况下,该输出与状态变量、输入量之间的函数关系式,称为系统的输出方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
= [ 1
0
⋯
x1 x 2 + 0 ] ⋮ x n
[β ]u
0
5.频域描述化为状态空间描述 (1)控制系统传递函数的极点为两两相异
ɺ x1 s1 x ɺ2 = ⋮ ɺ x n1 0 y = [k 1 k 2 s2 ⋱ 0 sn x 1 1 x 1 2 + u ⋮ ⋮ x n 1
y = [C 1
x 0 ] 1 x2
子系统的传递函数矩阵为
G i ( s ) = C i ( sI − Ai ) −1 Bi
i=1,2
y ( s ) = y1 ( s ) = G1 ( s )[u ( s ) − G2 ( s ) y ( s )] = G1 ( s )u ( s ) − G1 ( s )G2 ( s ) y ( s )
(3)状态空间 以n个状态变量作为基底所组成的n维空 间称为状态空间。 (4)线性系统 若在系统的状态空间表达式中,f和g均是 线性函数,则称系统为线性系统,否则为 非线性系统 (5)状态空间表达式 状态方程与输出方程的组合称为状态空 间表达式,又称动态方程。其一般形式为
x (t ) =
•
f [ x ( t ), u ( t ), t ]
(2)方程中包含输入函数的导数
y
(n)
+ a1 y (0) ⋯ + an −1 y + an y = b0 u +
( n −1)
•
( n)
+ b1 u
( n −1)
+ ⋯ + bn −1 u + bn u
•
状态方程
• x1 • x = 2 ⋮ • − xn
y = [k 11 k 12
⋯
k1n
]
x1 x 2 ⋮ xn
(3)传递函数的极点为k个重根 (4)传递函数同时具有单极点和重极点
6.跟据状态变量图列写线性系统的状态空间 描述 7.系统方块图导出状态空间描述 • 组合系统的状态空间描述:由两个或两个以上 组合系统的状态空间描述:
的子系统, 的子系统,按一定方式联接构成的系统称为组合 系统。 系统。 串联、并联、 串联、并联、反馈三种类型 • 子系统的并联
•
x
A x +B u y =C x +D u
n× n n× r
m×n m×r
•
=
(7) 状态空间分析法 在状态空间中以状态向量或状态变量描 述系统的方法称为状态空间分析法或状态 变量法。 状态空间分析法的优点是便于采用向量、 矩阵记号简化数学描述,便于在数学机上 求解,容易考虑初始条件,能了解系统内 部状态的变化特征,适用于描述时变、非 线性、连续、离散、随机、多变量等各类 系统,便于应用现代设计方法实现最优控 制、自适应控制等。
线性系统的状态空间描述
1.系统的数学描述 (1)系统的外部描述,即输入——输出 描述。 (2)系统的内部描述,即状态空间描述。 2.状态空间描述的组成 (1)状态方程 x 、u间因果关系 (2)输出方程 x 、u与y间转换关系 注:x状态变量 u输入变量 y输出变量
3.系统状态空间描述常用的基本概念 (1)状态和状态变量 系统在时间域中的行为或运动信息的集 合称为状态。确定系统状态的一组独立变 量称为状态变量。 (2)状态向量 把描述系统状态的n个状态变量x1(t), x2(t),…,xn(t)看作向量x(t)的分量,即 X(t)=[x1(t),X2(t),…,xn(t)] T 则向量X(t)称为n维向量。
⋯
x1 x k n ] 2 ⋮ xn
(2)传递函数的极点为一个重根
ɺ x1 x ɺ 2 ⋮ ɺ xn s1 = 0 1 s1 1 ⋱ 0 1 s1 x1 x 2 ⋮ xn 0 0 + u ⋮ 1
1 0 ⋮
0 1 ⋮
⋯ ⋯
− a n −1 − a n− 2
0 x1 0 0 x2 0 + ⋮ ⋮ ⋮ u ⋯ − a1 xn bn
输出方程 y
= [1
0
⋯
x1 0 ] x 2 ⋮ x n
4.一般时域描述化为状态空间描述 (1)方程中不包含输入函数的导数
y
(n)
+
a y
1
( n −1 )
+⋯ +
a
n −1Biblioteka y+a•n
y =
b u
n
状态方程
• 0 x1 • 0 x = 2 ⋮ ⋮ • − an xn
y ( t ) = g [ x ( t ), u ( t ), t ]
(6)线性系统的状态空间表达式 线性系统的状态方程是一阶向量线性微 分方程或一阶向量线性差分方程,输出方 程是向量代数方程。线性连续时间系统状 态空间表达式的一般形式为 线性时变系统 线性定常系统
x(t) = A(t)x(t) + B(t)u(t) y(t) = C(t)x(t) + D(t)u(t)
= u ( s ) − G2 ( s ) y1 ( s ) = u ( s ) − G2 ( s )G1 ( s )u1 ( s )
且:y ( s) = y1 ( s) = G1 ( s)u1 ( s) 假定:det( I + G2 ( s )G1 ( s)) ≠ 0 则得另一种表达式为:
G ( s ) = G1 ( s )[ I + G2 ( s)G1 ( s )]−1
G(s) = G 2 (s)G 1 (s)
• 子系统的反馈联接
子系统 D i = 0 条件
状态空间描述
• x1 = A 1 x1 + B1u − B1C 2 x 2 • x 2 = A 2 x 2 + B 2 C 1 x1 y = C 1 x1
• x1 A1 ∑F : • = B C x 2 1 2 − B1C2 x1 B1 + u A2 x2 0
x y = [C1 C2 ] 1 + [D1 + D2 ]u x2
传递函数矩阵为 G (s ) = ∑ Gi ( s)
i =1
2
可推广至N个子系统的并联组合系统 • 子系统的串联
串联的条件
动态方程
• x 1 = A1 x1 + B 1u • x 2 = A 2 x 2 + B 2 C 1 x1 + B 2 D 1u y = C x + D C x + D D u 2 2 2 1 1 2 1
0 0 ⋮
1 0 ⋮ −
0 1 ⋮
⋯ ⋯ ⋯
a
n
a
n −1
−a
n−2
0 x1 β 1 0 x 2 β 2 + ⋮ ⋮ ⋮ − a 1 x n β n
[u ]
输出方程 y
∑ : xi
i
•
= Ai x i + B i u i
yi = Ci xi + Di ui i=1,2 并联的条件
Dim()表示向量()的维数 并联后 u = u = u
1 2
y1 = y 2 = y
• 动态方程为 x 1 = A1 x 1 + B 1u • x 2 = A2 x 2 + B 2u y = C x + C x + (D + D )u 1 1 2 2 1 2 • 状态空间描述 ∑ p : x1 = A1 0 x1 + B1 u • 0 A x B 2 2 2 x 2
状态空间描述
• 0 x1 B1 x A : •1 = 1 + u ∑T B2C1 A2 x2 B2 D1 x 2
y = [D2C1
x1 C2 ] + ( D1D2 )u x2
传递函数矩阵为
化简 [I + G1 (s)G2 (s)]y(s) = G1 (s)u(s) 若 det(I + G1 (s)G2 (s)) ≠ 0 得反馈系统的传递函数矩阵为
G ( s ) = [ I + G1 ( s)G2 ( s )]−1 G1 ( s )
另:u1 ( s) = u ( s) − y2 ( s) = u ( s) − G2 ( s)u ( s)
