竖曲线要素及变坡点处设计高程计算
竖曲线要素及变坡点处设计高程计算

竖曲线要素及变坡点处设计高程计算 坡度计算:①坡度=高差坡长②竖曲线类型:当1n n i i +-为正值时,为凹型竖曲线; 当1n n i i +-为负值时,为凸型竖曲线。
③由厘米坐标纸上,经过反复试坡、调坡, 根据土石方填挖大致平衡和道。
设计规范中最小坡长等设计要求最后确定出变坡点: 变坡点1桩号:67.2550+K ,高程m 9404.0- 变坡点计算 ①变坡点一:桩号 67.2550+K , %150.0-i 1= %220.0i 2= R= 变坡点高程:m 9404.0- A.计算竖曲线要素:=-=1i 2i ω% 此时根据规范可知:该曲线为凹形曲线竖曲线几何要素中曲线长)(m R L 80%37.021621=⨯=⨯=ω 竖曲线几何要素中切线长m L T 402802=== 竖曲线几何要素中外距m R T E 037.062.21621240222=⨯==B.计算竖曲线起终点桩号 竖曲线起点桩号:67.2150+K竖曲线起点高程:m 8804.0-%15.0409404.0-=⨯+ 竖曲线终点桩号:67.2950+K竖曲线终点高程:m 8524.0-%22.0409404.0-=⨯+计算设计高程由110()H H T X i =-- H=H 1±hH 1:任一点切线的高程 x :计算点到起点的距离 i 1:坡度H:任一点的设计高程曲线段内各点的设计高程: K0+220X== m Rx y 0004.022== 切线高程: 设计高程:+= K0+240X= m Rx y 0137.022== 切线高程: 设计高程:+= K0+260X= m Rx y 0294.022== 切线高程: 设计高程:+= K0+280X= m Rx y 0057.022== 切线高程: 设计高程:+=直线段内各点设计高程见下表:设计高程表 桩号 高程(m )桩号高程(m )K0+000 ++ + ++++ ++ ++ ++ ++ ++ ++ ++ ++。
道路曲线高程计算公式

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:。
竖曲线计算公式

竖曲线计算公式竖曲线计算公式加强版缓和曲线、竖曲线、圆曲线、匝道(计算公式)一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH 点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH 点的切线方位角:α⑥点ZH 的坐标:xZ ,yZ说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n 的取值如下:当计算第二缓和曲线上的点坐标时,则:l 为到点HZ 的长度α为过点HZ 的切线方位角再加上180°K 值与计算第一缓和曲线时相反xZ ,yZ 为点HZ 的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH 点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH 点的切线方位角:α⑥点ZH 的坐标:xZ ,yZ说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n 的取值如下:当只知道HZ 点的坐标时,则:l 为到点HZ 的长度α为过点HZ 的切线方位角再加上180°K 值与知道ZH 点坐标时相反xZ ,yZ 为点HZ 的坐标三、曲线要素计算公式公式中各符号说明:l ——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度) l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R ——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S 、SZ 为里程数据,往往有些人计算时误入,用等实际计算的距离计算!!五、超高缓和过渡段的横坡计算第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1三、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:xy②待求点的切线方位角:αT注:sgn(x)函数是取符号函数,当x0时sgn(x)=1,当x=0时sgn(x)=0。
竖曲线

竖曲线是在变坡点处,为了行车平顺的需要而设置的一段曲线。
竖曲线的形状,通常采用圆曲线或二次抛物线两种。
在设计和计算上抛物线比圆曲线更为方便,故一般采用二次抛物线。
在纵坡设计时,由于纵断面上只反映水平距离和竖直高度,因此竖曲线的切线长与弧长是其在水平面上的投影,切线支距是竖直的高程差,相邻两条纵坡线相交角用坡度差表示。
一、竖曲线要素计算如图3-3所示,设变坡处相邻两纵坡度分别为i1和i2,坡度差以ω表示,则坡度差ω为i1和i2的代数差,即ω= i1-i2:当ω>0时,则为凸形竖曲线;当ω<0时,则为凹形竖曲线。
图3-3竖曲线示意图1、竖曲线的基本方程二次抛物线作为竖曲线的基本形式是我国目前常用的一种形式。
如图3-4所示,用二次抛物线作为竖曲线的基本方程:3-4 竖曲线要素示意图竖曲线上任意一点的斜率为:当x=0时:k= i1,则b= i1;当x=L,r=R时:,则:因此,竖曲线的基本方程式为:或 (3-19)2、竖曲线的要素计算曲线长:(3-20)切线长:(3-21)外距:(3-22)曲线上任意一点的竖距(改正值):(3-23)二、竖曲线设计标准竖曲线的设计标准包括竖曲线的最小半径和最小长度。
1、竖曲线设计的限制因素(1)缓和冲击汽车在竖曲线上行驶时会产生径向离心力,在凸形竖曲线上行驶会减重,在凹形竖曲线上行驶会增重,如果这种离心力达到某种程度时,乘客就会有不舒适的感觉,同时对汽车的悬挂系统也有不利影响,故应对径向离心力加速度加以控制。
根据试验得知,离心加速度a限制在0.5~0.7m/s2比较合适。
汽车在竖曲线上行驶时其离心加速度为:(3-24)《标准》中确定竖曲线半径时取a=0.278 m/s2。
或(3-25)(2)行程时间不宜过短汽车从直坡段驶入竖曲线时,如果其竖曲线长度过短,汽车倏忽而过,冲击力大,旅客会感到不舒适,太短的竖曲线长度从视觉上也会感到线形突然转折。
因此,应限制汽车在竖曲线上的行程时间,一般不宜小于3s。
竖曲线

竖曲线1、竖曲线要素计算1.)变坡角δ:相邻两纵坡i1,i2,由于公路纵坡的允许值不大,故可以认为变坡角δ为:δ=△i= i1-i2(若不考虑近似情况,该值δ=arctan (i1)-arctan(i2)。
需要注意的是假设坡度上升为正时,δ计算结果会有正有负,但其绝对值的大小却与变坡角的角度相等。
但若不考虑正负差异,会造成最终的计算结果出错。
)2.)切线长T:(变坡角δ和圆心角大小相等。
)由于δ很小,可认为故(若不考虑近似情况,,δ值的正负号需注意。
)3.)曲线长L的计算由于变坡角δ很小,可认为L=2T(若不考虑近似情况,因为δ等于该弧所对应的圆周角,那么L=R*δ,其中δ应换算成弧度。
注意在利用CASIO计算器计算时的中间、最终结果的角度弧度问题。
)4.)外矢距E的计算由于变坡角δ很小,可认为y坐标与半径方向一致,它是切线上与曲线上的高程差。
从而得(R+y)2=R2+x2展开2Ry=x2-y2又因y2 与x2相比较,y2的值很小,略去y2,则2Ry= x2即当x=T时,y值最大,约等于外矢距E,所以(若不考虑近似情况,y2+2Ry-x2=0,,其中E >0,。
)2、竖曲线的测设算例:已知:某竖曲线半径R=2000米,相邻坡段的坡度i1=-2.95%,i2=-5.0628%,变坡点里程桩号为K0+760,其高程为428.312米。
(设计给出T=21.128,E=0.112。
)求:K0+730、K0+740、K0+750、K0+760、K0+770、K0+780、K0+790的线路坡度高程和设计高程。
解:步骤一:由已知条件知δ= i1-i2=-0.0295+0.050628=0.021128弧度(若不考虑近似情况δ=(arctan(i1)-arctan(i2))=1°12′30.82″=0.0210940493155弧度)1、)切线长=1000*(-0.0295+0.050628)=21.128米(若不考虑近似情况,=21.0942米)2、)曲线长L=2T=21.128*2=42.256米(若不考虑近似情况L=R*δ=2000*(arctan(i1)-arctan(i2))=2000*1°12′30.82″*π/180°=42.1867米)3、)外矢距=21.128^2/4000=0.1116米(若代入T=21.0942,计算结果=0.1112)(若不考虑近似情况 =0.1112米,其中T=21.0942。
竖曲线高程计算公式推导过程及计算流程

竖曲线⾼程计算公式推导过程及计算流程竖曲线⾼程计算公式推导及计算流程1. 竖曲线介绍竖曲线是指在纵断⾯内,两个坡线之间为了延长⾏车视距或者减⼩⾏车的冲击⼒,⽽设计的⼀段曲线。
⼀般可以⽤圆曲线和抛物线来充当竖曲线。
由于圆曲线的计算量较⼤,所以,通常采⽤抛物线作为竖曲线,以减少计算量。
2. 竖曲线⾼程计算流程竖曲线计算的⽬的是确定设计纵坡上指定桩号的路基设计标⾼,其计算步骤如下:a. 计算竖曲线的基本要素:竖曲线长L ;切线长T ;外失距Eb. 计算竖曲线起终点的桩号:竖曲线起点的桩号=变坡点的桩号-Tc. 计算竖曲线上任意点切线标⾼及改正值:切线标⾼=变坡点的标⾼±(x T -)?i 改正值:221x Ry =d. 计算竖曲线上任意点设计标⾼某桩号在凹形竖曲线的设计标⾼ = 该桩号在切线上的设计标⾼+ y 某桩号在凸形竖曲线的设计标⾼ = 该桩号在切线上的设计标⾼-y3. 竖曲线⾼程计算公式推导已知条件:第⼀条直线的坡度为1i ,下坡为负值,第⼀条直线的坡度为2i ,上坡为正值,变坡点的⾥程为K ,⾼程为H ,竖曲线的切线长为B A T T T ==, 待求点的⾥程为X K 曲线半径R竖曲线特点:抛物线的对称轴始终保持竖直,即:X 轴沿⽔平⽅向,Y 轴沿竖直⽅向,从⽽保证了X 代表平距,Y 代表⾼程。
抛物线与相邻两条坡度线相切,抛物线变坡点两侧⼀般不对称,但两切线长相等。
竖曲线⾼程改正数计算公式推导设抛物线⽅程为:()021≠++=a c bx ax y设直线⽅程为:()02≠+=k b kx y由图可知,抛物线与直线都经过坐标系222Y O X 的原点2O ,所以可得:00==b c ;分别对21y y 、求导可得:b ax y +=2'1k y ='2当0=x 时,由图可得:b i y ==1'1k i y ==1'2当L x =时,由图可得:12'12i aL i y +==由上式可得:RL L i i a 212212==-=ω所以抛物线⽅程为:x i x Ry 12121+=直线⽅程为:x i y 12=对于竖曲线上任意⼀点P ,到其切线上Q 点处的竖直距离,即⾼程改正数y 为:21122121X RX i X i X R y y y P Q =-+=-= 竖曲线曲线元素推导竖曲线元素有切线长T 、外失距E 和竖曲线长L 三个元素,推导过程如下:由图可知:2tan ω=R T 由于转⾓ω很⼩,所以可近似认为22tan ωω=,因此可得:2ωR T = 由图易得:ωR L =将切线长T 带⼊到221x Ry =中可得外失距RT E 22=4. 曲线⾼程计算⽰例已知:某条道路变坡点桩号为K25+460.00,⾼程为780.72.m ,i1=0.8%,i2=5%,竖曲线半径为5000m 。
高速公路的一些线路坐标、高程计算公式

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。
竖曲线计算
K5+100.00:位于下半支
②按变坡点分界计算:
横距x2= (k5+120.00)– (k5+100.00) =20m
竖距
y2 x2
2
20
2
2R
2 2000
0 . 10
切线高程 H1 = H0 - i2( T - x) = 427.68 - 0.04×(90 - 20) = 424.88m
横距x2= (K5+100.00 )–(K4+940.00)=160m 竖距
y2 x2
2
160
2
2R
2 2000
6 . 40
切线高程 H1 = H0 -i1( T - x) = 427.68 -0.05×(90 - 160) = 431.18m
设计高程 H = H1 – y2 = 431.18 – 6.40 = 424.78m
H 1 H 0 T x i
(3)任一点设计高程计算
式中 H0——变坡点标高(m); H1——计算点切线高程(m); “±”凹形竖曲线取“+”, i——纵坡度的绝对值。 凸形竖曲线取“-”。
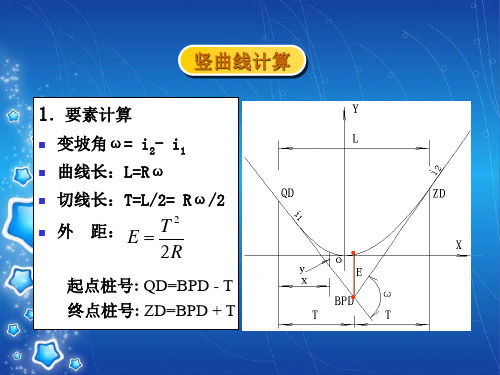
[例]:某山岭区一般二级公路,变坡点桩号k5+030.00, 高程H0=427.68m,i1=+5%,i2=-4%,竖曲线半径R=2000m。 试计算竖曲线诸要素以及桩号为k5+000.00和k5+100.00处 设计高程。 解:1.计算竖曲线要素 ω=i2- i1= - 0.04-0.05= - 0.09<0,为凸形。 曲线长 L = Rω=2000×0.09=180m
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
竖曲线要素及变坡点处设计高程计算
坡度计算:
①坡度=高差坡长
②竖曲线类型:当1n n i i +-为正值时,为凹型竖曲线;
当1n n i i +-为负值时,为凸型竖曲线。
③由厘米坐标纸上,经过反复试坡、调坡, 根据土石方填挖大致平衡和道。
设计规范中最小坡长等设计要求最后确定出变坡点:
变坡点1桩号:67.2550+K ,高程m 9404.0-
变坡点计算
①变坡点一:
桩号 67.2550+K , %150.0-i 1= %220.0i 2= R=21621.62m 变坡点高程:m 9404.0-
A.计算竖曲线要素:
=-=1i 2i ω0.37% 此时根据规范可知:该曲线为凹形曲线
竖曲线几何要素中曲线长)
(m R L 80%37.021621=⨯=⨯=ω 竖曲线几何要素中切线长m L T 402
802=== 竖曲线几何要素中外距m R T E 037.062
.2162124022
2=⨯== B.计算竖曲线起终点桩号
竖曲线起点桩号:67.2150+K
竖曲线起点高程:m 8804.0-%15.0409404.0-=⨯+
竖曲线终点桩号:67.2950+K
竖曲线终点高程:m 8524.0-%22.0409404.0-=⨯+
计算设计高程
由1
10()H H T X i =-- H=H 1±h H 1:任一点切线的高程
x :计算点到起点的距离
i 1:坡度
H:任一点的设计高程
曲线段内各点的设计高程:
K0+220
X=220-215.67=4.33m m R
x y 0004.022
== 切线高程:-0.8804-4.33×0.15%= -0.8869m 设计高程:-0.8869+0.0004= -0.8865m K0+240
X=24.33m m R
x y 0137.022
== 切线高程:-0.8804-24.33×0.15%= -0.9169m 设计高程:-0.9169+0.0137= -0.9032m K0+260
X=35.67m m R
x y 0294.022
== 切线高程:-0.8524-35.67×0.22%= -0.9309m 设计高程:-0.9309+0.0294= -0.9015m K0+280
X=15.67m m R
x y 0057.022
== 切线高程:-0.8524-15.67×0.22%= -0.8869m 设计高程:-0.8869+0.0057= -0.8812m 直线段内各点设计高程见下表:
设计高程表
桩号
高
程(m ) 桩号 高程(m ) K0+000
-0.56 +240.000 -0.9032 +20.000
-0.59 +260.000 -0.9015 +40.000 -0.62 +280.000 -0.8812
+60.000 -0.65 +300.000 -0.8361 +80.000 -0.68 +320.000 -0.7921 +100.000 -0.71 +340.000 -0.7481 +120.000 -0.74 +360.000 -0.7041 +140.000 -0.77 +380.000 -0.6601 +160.000 -0.80 +400.000 -0.6161 +170.000 -0.83 +420.000 -0.5721 +180.000 -0.86 +440.000 -0.5281 +200.000 -0.89
+220.000 -0.8865。
