《结构力学》第十一章 影响线及其应用
结构力学章节习题及参考答案
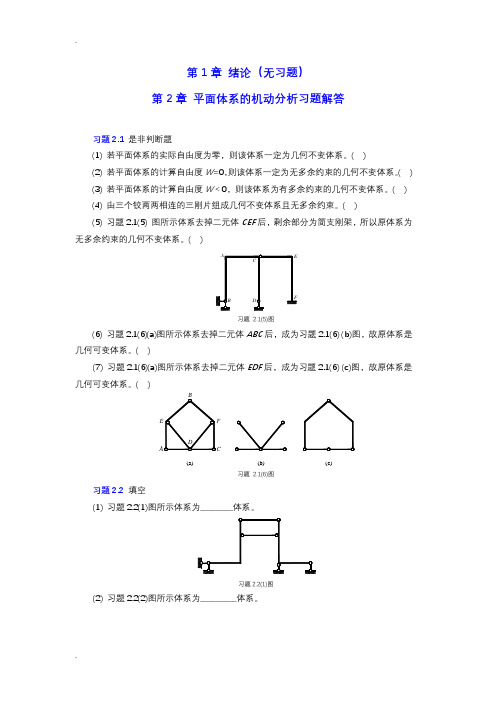
习题3.1是非判断题
(1) 在使用内力图特征绘制某受弯杆段的弯矩图时,必须先求出该杆段两端的端弯矩。( )
(2) 区段叠加法仅适用于弯矩图的绘制,不适用于剪力图的绘制。( )
(3) 多跨静定梁在附属部分受竖向荷载作用时,必会引起基本部分的内力。( )
(4)习题3.1(4)图所示多跨静定梁中,CDE和EF部分均为附属部分。( )
(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后,成为习题2.1(6) (c)图,故原体系是几何可变体系。( )
习题 2.1(6)图
习题2.2填空
(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图
(2) 习题2.2(2)图所示体系为__________体系。
习题 2-2(2)图
(4)习题5.1(3)图(a)和(b)所示两结构的变形相同。( )
习题7.2填空题
(1)习题5.2(1)图(a)所示超静定梁的支座A发生转角,若选图(b)所示力法基本结构,则力法方程为_____________,代表的位移条件是______________,其中1c=_________;若选图(c)所示力法基本结构时,力法方程为____________,代表的位移条件是______________,其中1c=_________。
(3) 习题7.2(3)图所示刚架各杆的线刚度为i,欲使结点B产生顺时针的单位转角,应在结点B施加的力矩MB=______。
习题 7.2(1)图习题 7.2(2)图 习题 7.2(3)图
(4) 用力矩分配法计算习题7.2(4)图所示结构(EI=常数)时,传递系数CBA=________,CBC=________。
中南大学结构力学课件 11影响线及其应用

结构力学
C B
b
F =1
a l
F yB
当荷载F=1在截面C的左方移动时,为了计算简便, 取梁中CB段为隔离体,并规定以使梁下面纤维受拉 的弯矩为正,由∑MC = 0 ,得
由此可知,MC 的影响线在截面C 以左部分为一直 线,由两点的纵坐标 ab x 0,M C 0 x a,M C l 即可绘出AC 段MC 的 影响线。
F1
F2
静力法——静力平衡条件; 机动法——虚位移原理。
中南大学
退出
返回
07:34
§11-2 用静力法作静定梁的影响线
用静力法作静定梁影响线的基本步骤:
结构力学
1. 建立坐标系。选取坐标原点,以F=1的移动 方向为x轴(x 轴的指向可以任意假设),以与F=1 指向相反的方向作为y 轴正方向建立坐标系。 2. 建立静力平衡方程,将该量值表示为x 的函数。
中南大学
退出
返回
07:34
§11-2 用静力法作静定梁的影响线
F =1 x
D K A C B
结构力学
E
d
a
b
当荷载F=1在截面K的右方移动时,任取截面K以 左部分为隔离体,则
M K 0 FSK 0
据此可绘出弯矩MK和剪力FSK 影响线。 只有当荷载作用在DA段时,才对MK 、 FSK 有影响。
分析弯矩影响线方程可以看出,MC的左直线为反力FyA 的影响线将纵坐标乘以b而得到,右直线可由反力 FyB 的影 响线将纵坐标乘以a而得到。因此,可以利用 FyA 和 FyB的 影响线来绘制弯矩MC的影响线:在左、右两支座处分别取 纵坐标a 、 b,将它们的顶点各与右、左两支座处的零点用 直线相连,则这两根直线的交点与左、右零点相连部分就 是MC的影响线。这种利用已知量值的影响线来作其他量值 影响线的方法,能带来较大的方便。
结构力学影响线讲解共50页文档

61、奢侈是舒适的,否则就不是奢侈 。——CocoCha nel 62、少而好学,如日出之阳;壮而好学 ,如日 中之光 ;志而 好学, 如炳烛 之光。 ——刘 向 63、三军可夺帅也,匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里,与其说好 的教师 是幸福 ,不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战,就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿
谢谢!
结构力学影响线讲解
•
6、黄金时代是在我们的前面,而不在 我们的 后面。
•
7、心急吃不了热汤圆。
•
8、你可以很有个性,但某些时候请收 敛。
•ห้องสมุดไป่ตู้
9、只为成功找方法,不为失败找借口 (蹩脚 的工人 总是说 工具不 好)。
•
10、只要下定决心克服恐惧,便几乎 能克服 任何恐 惧。因 为,请 记住, 除了在 脑海中 ,恐惧 无处藏 身。-- 戴尔. 卡耐基 。
结构力学

4-1 解:(1) F YA 影响线00YY P FF F =⇒-=∑1Y P F F ⇒==(2) M A 影响线00(0)AA P MM F x x l =⇒+⨯=≤≤∑A M x ⇒=-(3) M C 影响线当F P 作用在C 点左边时,取右半部分有:0(0)C M x a =≤≤当F P 作用在C 点右边时,取右半部分有:()10()C C M x a M a x a x l +-⨯=⇒=-≤≤(4) F QC 影响线当F P 作用在C 点左边时,取右半部分有: 0QC F =当F P 作用在C 点右边时,取右半部分有: 1QC F =4-3 解:(1) M A 影响线当F P 作用在BC 段时,取ABC 有:00(0)AA P MM F x x l =⇒+⨯=≤≤∑A M x ⇒=-当F P 作用在CE 段时,取CE 有:0()0()00LQC L QC D P A A M F b F l b x l x M M F l ⎧=⇒⨯-⨯+-=≤⎪⎨=⇒+⨯=⎪⎩∑∑()/A M l b x l b ⇒=-+-(2) Y A 影响线当F P 作用在BC 段时:1YA F =当F P 作用在CE 段时:()/YA F l b x b =+-ACBaLbxp F =1Lbc(3) M K 影响线当F P 作用在BK 段时:0K M =当F P 作用在KC 段时:K M l k a =-- 当F P 作用在CE 段时:()/K M l b x b a =+-(4) F QK 影响线当F P 作用在K 点左边时:0QC F = 当F P 作用在K 点左边时:QC YA F F = 4-8 解:(1) F RA 影响线当F P 作用在I 点时,F RA =0。
当F P 作用在A 点时, F RA =1 当F P 作用在E 点时, F RA =1 当F P 作用在B 点时, F RA =0 当F P 作用在F 点时, F RA =-1当F P 作用在G 、C 、D 、H 、J 点时, F RA =0 (2) F RB 影响线当F P 作用在I 、A 、E 点时, F RB =0 当F P 作用在B 点时, F RB =1 当F P 作用在F 点时, F RB =2当F P 作用在G 、C 、D 、H 、J 点时, F RB =0 (3) M A 影响线当F P 作用在I 、A 点时, M A =0 当F P 作用在E 点时, M A =-2 当F P 作用在B 点时, M A =0 当F P 作用在F 点时, M A =2当F P 作用在G 、C 、D 、H 、J 点时, M A =0 4-9 解:I :当荷载上承时当F P 作用在C 点左边时,取右半部分有:105IN RF M FF =⇒=-∑,20YN RF F F =⇒=∑,306C N RF M F F =⇒=∑ 当F P 作用在C 点右边时,取左半部分有:105IN RA M FF =⇒=-∑,20YN RA FF =⇒=∑ ,304C N RA M F F =⇒=∑F N1影响线12×1m=12mF N2影响线F N3影响线II :当荷载下承时 同理(略)4-14 解:(1) F RA 影响线 撤去支座A ,并使A 点向上发生单位虚位移,得F RA 的影响线。
结构力学第11章 影响线

x
P=1 1/2
x+ d
-
3d 4
1/4
D
QCE. I.L
M C .I .L
11-4 机动法绘作静定梁的影响线 一、刚体体系的虚功原理 刚体体系的虚功原理:刚体体系在力系作用下处于平 衡的充分必要条件是所有作用于刚体体系上的外力在刚 体体系的任意虚位移上做的虚功总和等于零。
W外 = 0
虚功方程
二、机动法绘制简支梁影响线 (1)反力影响线
A
x
P=1 B l d 1 B RB
证明:根据W外=0
FB 1 1 d 0
A
+
d FB
RB影响线
此式表明δ的值恰好就是单位力在x时B点的反力 值,刚好与影响线定义相同。(注意:δ是x的函数)
(2)弯矩影响线
x P=1 C l 1d + B b
0 4d MD RB h h
P=1 C D I
RA
l=6d
E
NDEE
F P=1 F
G
RB
A
C
D
G
B
x
2)当P=1在结点E以右移动时,取截面I-I以左部分为隔离体。
1、静力法
作图a所示多跨静 定梁MK的影响线,图 b为其层叠图。
F=1在AC段移 动时,MK=0,只考 虑荷载在CF段移动。 荷载在EF段移 动时的计算如图c。 荷载在CE段移动 时的计算同伸臂梁。
MK的影响线如图d。
多跨静定梁任一反力或内力影响线的作法
(1)F=1在量值本身所在梁段上移动时,量值影响线与相应 单跨静定梁相同。
MD=0 当P=1位于D截面左侧时,
当P=1位于D截面右侧时,
QD影响线 MD影响线
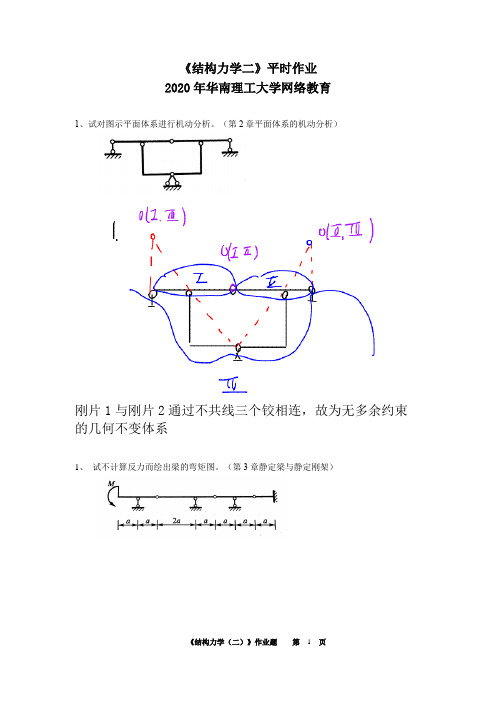
《结构力学二》平时作业-2020年华南理工大学网络教育
3、图示抛物线三铰拱的轴线方程为 ,试求截面K的内力。(第4章静定拱)
4、试用截面法计算图示桁架中指定杆件的内力。(第5章静定平面桁架)
5、作图示结构的M图,并求链杆的轴力。(第5章静定平面桁架)
6、图示简支刚架支座B下沉b,试求C点水平位移。(第6章结构位移计算)
7、图示结构的支座B发生了水平位移 (向右), (向下), 。已知各杆的 , 。试:(a)作M图;(b)求D点竖向位移及F点水平位移。(第7章力法)
《结构力学二》平时作业
2020年华南理工大学网络教育
1、试对图示平面体系进行机动分析。(第2章平面体系的机动分析)
刚片1与刚片2通过不共线三个铰相连,故为无多余约束的几何不变体系
1、试不计算反力而绘出梁的弯矩图。(第3章静定梁与静定刚架)
2、作图示结构的 图,并求a杆的轴力。q=20kN/m。(第3章静定梁与静定刚架)
8、用力法计算,并绘图示结构的M图。EI=常数。(第7章力法)
9、用力法计算图示结构,作其M图。EI=常数。(第7章力法)
10、用位移法计算图示结构,并作M图。EI=常数。(第8章位移法)
11、已知图示结构B点的转角 ,各杆EI=常数,作M图。P=8kN,q=12kN/m。(第8章位移法)
12、试用位移法计算刚架,绘制弯矩图。E=常数。(第8章位移法)
13、试用力矩分配法计算图示刚架,并绘制M图。E=常数。(第9章渐近法)
14、用力矩分配法计算并Байду номын сангаас图示结构M图。EI=常数。(第9章渐近法)
15、试作图示伸臂梁 影响线。(第11章影响线及其应用)
结构力学 影响线及其应用
曲线即得内力包络图。
例:绘制简支梁在两台吊车作用下的弯矩包络图和剪力包络图。
P1
A
3.5m
P2 P3
1.5
3.5m
P4
P1 P2 P3 P4 82kN
B
RA
0 1.2 2.4
215
12m 6.0
RB
12m
弯矩包络图(kN· m)
366
465
559 94.3
65.0
574 41.7
25.3
f
b
4
A C D
E P=1
F
B
l=6a
4a/3 +
(a)
+ (b)
M C .IL
N 5 .IL
a
§8-3 用机动法做影响线
用机动法作静定结构内力(反力)影响线的理论基础是刚体系虚功原理。
机动法作内力(反力)影响线步骤如下:
1、去除与所求量值相应的约束,并代以正向的约束力。 2、使所得体系沿约束力的正方向发生相应的单位位移, 由此得到的P =1作用点的位移图即为该量值的影响线。 3、基线以上的竖标取正号,以下取负号。
只有当一个荷载通过影响线 顶点时,S`才有可能变号 令PK通过影响线顶点时,使S`变号,且使S取得极大值。 即:PK位于影响线顶点时;S`=0 左移荷载时:S`>0 右移荷载时:S`<0 用式子表示:
P1 P 2 PK PK 1 PN h 0 a b P1 P 2 PK 1 PK PK 1 PN h 0 a b
同理可以判定P4不是PK
MK max 1610 kN .m
结构力学—影响线

0.75 1.0
P1
P2
RB P1 y1 P2 y2
l
RB
定义:当单位荷载(P=1)在结构上移动时,表示结构某一指
定2截021/面6/24中某项内力变化规律的曲线,称为该项内力的影响线6 。
无论是研究结构在移动荷载作用下的内力变化规律或最不利荷载 位置,内力影响线都是最基本的工具。
影响线有两种画法;静力法和机动法。
B
dx
b
l
a
y
l
QC P1 y1 P2 y2 P3 y3
I.L QC
B
QC
q dx y
A
B
qA ydx
I.L QC
q AB
AB-影响线面积代数和
24
二、求荷载的最不利位置
如果荷载移到某一个位置,使某一指定内力达到最大值(+、-), 则此荷载所在位置称为最不利位置。
我们可以利用影响线来确定最不利位置,对比较简单的情况可以直观 地判断最不利位置。
c
5.6m
3m
6m
3m
14m
1.8m
3.36m
d
4m
8m
1.6m
I .L M C
设 PK 15kN 置于截面C处由判别式有:
x
0,
Ri
tgi
10
15
3.36 5.6
5
20
3.36 8.4
5
0
x
0,
Ri
tg i
10
3.36 5.6
15
5
20
3.36 8.4
10
0
Mmax 83kN m
2)确定内力的最大值及相应的荷载位置——最不利荷载位置。 方法:在各种荷载中抽象出单位荷载(P =1)。
李廉锟《结构力学》(上册)配套题库【课后习题】(影响线及其应用)【圣才出品】

第11章影响线及其应用复习思考题1.什么是影响线?影响线上任一点的横坐标与纵坐标各代表什么意义?答:(1)影响线是指当一个指向不变的单位集中荷载(通常是竖直向下的)沿结构移动时,表示某一指定量值变化规律的图形。
(2)横坐标代表单位集中荷载F=1的位置;纵坐标代表研究的一个反力或某一截面的某一项内力的量值。
2.用静力法作某内力影响线与在固定荷载作用下求该内力有何异同?答:用静力法作某内力影响线与在固定荷载作用下求该内力的异同点分别为:(1)相同点两者所用方法完全相同,即都是取隔离体由平衡条件来求该反力或内力。
(2)不同点用静力法作某内力影响线时,作用的荷载是一个移动的单位荷载,因而所求得的该反力或内力是荷载位置x的函数,即影响线方程;而在固定荷载作用下求该内力时,所求的就是某处的内力值。
3.在什么情况下影响线方程必须分段列出?答:当荷载作用在结构的不同部分上所求量值的影响线方程不同时,应将它们分段写出,并在作图时注意各方程的适用范围。
4.为什么静定结构内力、反力的影响线一定是由直线组成的图形?答:因为对于静定结构,其内力和反力影响线方程都是x的一次函数,故静定结构的反力和内力影响线都是由直线所组成的。
5.何谓间接荷载?如何做间接荷载下的影响线?答:(1)间接荷载是指对主梁来说,直接作用在其上面纵梁上的荷载。
(2)绘制间接荷载作用下影响线的步骤:①作出直接荷载作用下所求量值的影响线;②取各结点处的竖标,并将其顶点在每一纵梁范围内连以直线。
6.机动法作影响线的原理是什么?其中δP代表什么意义?答:(1)机动法作影响线的理论依据是虚位移原理,即刚体体系在力系作用下处于平衡的必要和充分条件是:在任何微小的虚位移中,力系所作的虚功总和为零。
(2)δP则为荷载F=1的作用点沿其方向的位移,由于F=1是移动的,因而δP就是荷载所沿着移动的各点的竖向虚位移图。
7.某截面的剪力影响线在该截面处是否一定有突变?突变处左右两竖标各代表什么意义?突变处两侧的线段为何必定平行?答:(1)截面的剪力影响线在该截面处一定有突变。
李廉锟《结构力学》(上册)配套题库【名校考研真题】(影响线及其应用)【圣才出品】

第11章影响线及其应用一、填空题1.在间接荷载作用下,梁截面内力影响线的作法是:应先作______截面内力影响线,然后再对该截面有影响的区段按直线规律变化修正。
[西南交通大学2006研] 【答案】直接荷载下该指定量值的影响线,而后按两横梁间为直线修改【解析】间接荷载下的影响线是以直接荷载作用下的影响线为基础的,具体作法:应先作直接荷载下该指定量值的影响线,而后按两横梁间为直线修改截面内力影响线,然后再对该截面有影响的区段按直线规律变化修正。
2.如图11-1所示多跨静定梁M D及F DQ的影响线分别为______,______(用图表示)。
[湖南大学2007研]图11-1【答案】;【解析】采用静力法。
以A 点为坐标原点,先求M D 的影响线当02x ≤≤时,M D =0;当24x ≤≤时,2D M x =-+;当48x ≤≤时,142D M x =-。
综上可画出M D 的影响线。
求F DQ 的影响线当02x ≤≤时,F DQ =0;当24x ≤≤时,1DQ F =+;当48x ≤≤时,124D M x =-+。
综上可画出F DQ 的影响线。
3.如图11-2所示组合结构,P =1在ABC 段移动,链杆DE 轴力的影响线在C 点处的竖标值为______。
[中南大学2005研]图11-2【答案】1【解析】链杆DE 轴力的影响线在C 点处的竖标值即为当C 点作用竖向单位力时DE 杆的轴力;显然结构为对称的,易知A 、B 支座的竖向反力均为1/2,;在C 点沿竖向截开,取右半部分为隔离体,根据平衡条件:0C M =∑,算得DE 杆的轴力为1。
二、选择题1.如图11-3所示三铰拱的拉杆N AB的影响线为()。
[浙江大学2007研]A.斜直线B.曲线C.平直线D.三角形图11-3【答案】D【解析】根据静力法判断,当P=1在AC段上时,N AB的值为B支座反力乘以一个常数(BC水平投影与拱高的比值),同理当P=1在CB段上时,N AB的值为A支座反力乘以一个常数(AC水平投影与拱高的比值);易知A、B支座反力的影响线为两个直角三角形,所以N AB的影响线为A、B支座反力的影响线乘以常数后的相交区域的三角形。
结构力学第11章

p
1
换句话说,在虚位移过程中 单位荷载位置的位移图 p(x)反映 了反力RB 随Fp=1荷载位置变化规 律。即位移图p(x)就代表了RB 的 影响线。
机动法作影响线的步骤: (a)欲求某一量值的影响线,解除与之相应的 约束,用相应未知量代替; (b)沿相应未知量方向上产生单位位移,则所 得位移图即为相应量的影响线。
§11.3
*间接荷载作用下
的影响线
上节中讨论影响线时,单位荷载都是直接作用于梁上, 故称直接荷载作用下的影响线。在实际工程中,还存在另 一种形式的荷载——间接荷载。如图(a)所示桥梁结构,主 梁承受间接荷载(又称结点荷载)作用。下面讨论间接荷 载作用下影响线的特点及绘制方法。 (1)容易证明,反力影响线 及结点处MC和MD的影响线 与直接荷载作用下的影响线 完全相同。
A
x Fp=1
C l B
RA
a
b
RB
图(a)
1
图(b) RA影响线
1
图(c) RB影响线
a b/
A
求任一截面C的弯矩MC影响线 ,易得
x M C RB b b l lx M C RA a a l
(0 x a) (b)
l
图(d) MC影响线
(a x l)
RA
1
图(c)
RB
RA:
图(d)
(2)影响线: 当一个方向不变的单位荷载(广义荷载)沿一结 构移动时,表示某一量值(反力、内力等)随荷载位 置变化规律的函数图形,称为该量值的影响线。 影响线是活载作用下结构分析计算的工具。 影响线的用途 (a)确定一组荷载对结构某一量值 的影响 (b)确定最不利荷载的位置及相应 的最大值 绘制影响线常用的方法有两种: 静力法 机动法
结构力学——影响线

10
铰结点的影响线
2010-12-11
此为绝密,不得外传!
11
2010-12-11
此为绝密,不得外传!
12
多跨梁的影响线
多跨梁要区分基本结构和附属结构,根 据基本结构和附属结构传力特点,绘制 影响线。 点在附属结构上,影响线对基本结构没 有影响;点在基本结构上,影响线对附 属结构有影响。
2010-12-11 此为绝密,不得外传! 13
2010-12-11
此为绝密,不得外传!
5
2010-12-11
此为绝密,不得外传!
6
2010-12-11
此为绝密,不得外传!
7
单跨梁的影响线
2010-12-11
此为绝密,不得外传!
8
固定端的影响线
2010-12-11
此为绝密,不得外传!
9
滑动支座影响线
2010-12-11
此为绝密,不得外传!
此为绝密,不得外传!
23
2010-12-11
此为绝密,不得外传!
24
2010-12-11
此为绝密,不得外传!
25
THE END! END! 再见! 再见!
2010-12-11 此为绝密,不得外传! 26
机动法作影响线
张志明 作
2010-12-11
此为绝密,不得外传!
1
弯矩影响线
添加铰结点,在铰结 点两侧添加弯矩。铰 结点左侧添加逆时针 的弯矩,右侧添加顺 时针的弯矩。 如右图
2010-12-11 此为绝密,不得外传! 2
剪力影响线
在该点添加滑动支座。 滑动支座右侧受到向 上的力,左侧受到向 下的力。 如右图
2010-12-11
结构力学第五版 李廉锟 第十一章影响线及其应用
第十一章 影响线及其应用
§11-4 机动法绘作静定梁的影响线
一、机动法做影响线的基本原理 刚体体系的虚功原理:虚位移原理(虚设单位位移法) • 机动法的优点:不经计算快速的绘出影响线的形状。从而确 定荷载的最不利位置。也可用它来校核静力 法绘制的影响线。 二、作图步骤 1.撤掉与所求量值相对应的约束(支座或与截面内力对 应的约束),用正方向的量值来代替; 2.沿所求量值正方向虚设单位位移,并画出整个梁的刚 体位移图; 3.应用刚体体系的虚功原理建立虚功方程,导出所求量 值与位移图之间的关系,即为影响线。
二者的区别:
(1)固定荷载作用下,结构内力与位移是确定的,截面内力是定值;
(2)在移动荷载作用下,结构内力随荷载位置的变化而变化。
工程实际中移动荷载的类型很多,但都具有大小和方向保 持不变的特性,抓住这一特点,从中取出移动的单位集中荷载 (F=1)进行研究,它是各种移动荷载中最简单、最基本的情 形。
将荷载 F=1放在任意位置,并选定一坐标 系,以横坐标 x表示荷载作用点的位置,然后 根据静力平衡条件求出所求量值与荷载位置 x 之间的函数关系,这种关系式称为影响线方程, 再根据方程作出影响线图形。
静力法: 与固定荷载作用: 求解相同——平衡条件求解反力、内力; 区别在于——荷载的位置为变量x ——反力、内力为x的函数——影响线方程 注意:影响线方程不同时,需分段写出; 作影响线图时,注意各方程的适用范围 静定结构——影响线直线: 直接法——分段直线方程的控制点,连直线 超静定结构——影响线一般为曲线
5 d 8
15 d 16
l=4d
3 d 4
RB
MC.I.L
+
x
MC
8
d
结构力学 第11章 影响线及其应用

2. 间接荷载影响线的绘制方法
F=1 F=1 F=1 A C D y E F=1 B
以绘制MC影响线为例
(1)首先,将F=1移动到各 结点处。 其MC与直接荷载作用 在主梁上完全相同。
yD
yE
F=1
x
d
MC影响线
dx d
x d
接荷载作用下MC影响线在D、 E处的竖标为 yD、yE , 在上述 两结点荷载作用下MC值为
S=F1y1+F2y2+…+Fnyn =(F1x1+F2x2+…+Fnxn)tg =tg∑Fixi
S影响线
F1
F2
R
Fn
据合力矩定理 ∑Fixi=R x
故有 S=R x tg=R y
合力
o
0 x
1
y1
x2
y2
y
yn S影响线
x
合力R作用点处影响线的竖标
2. 分布荷载 微段dx上的荷载为dx
则ab区段内分布荷载产生
的影响量:
dx
b
S=
b
a
q x ydx
a
y
b S影响线
q
均布荷载(Fs=常数)
S= q ydx q
a
a
ω
b
S影响线
影响线在荷载范围内面积的 代数和
§11—8 铁路和公路标准荷载制(P295,了解)
公路上行驶的汽车、拖拉机等类型繁多,载运情况复杂,设计 结构时不可能对每种情况都进行计算,而是以一种统一的标准 荷载来进行设计。这种标准荷载是经过统计分析制定出来的, 它既概括了当前各类车辆的情况,又适当考虑了将来的发展。
结构力学-影响线概念及应用

1
FQ2
A
1
2 B 3C
MB影响线 FQ3影响线
2m 1m 1m 1m 1m 1m 1m 2m
1
(
MB
2
1
1
4D 1m 1m
FQ3
A
1
2 B 3C
2m 1m 1m 1m 1m 1m 1m 2m
VC影响线 FQ4影响线
1
VC
4D 1m 1m
1
FQ4
A
1
2 B 3C
2m 1m 1m 1m 1m 1m 1m 2m
q(x) dx y(x)
D
E
qD y(x) d x
qA
x
q( A1 A2 )
例:求FQC。
FP=20kN q=10kN/m
A
B
CD
1.2 1.2 1.2 1.2 1.2
0.6
0.4 0.2
0.2 0.4
FQC 14kN
例:求C点左侧、右侧截面的剪力。
FP1
FP2
A
B
C
a b/2 b/2
(2) Influence Lines for Cantilever Beams
练习:作VA , MA , MC , FQC 的影响线。
MA
FP=1
A
B
C
a
b
A
VA a
MC
FP=1 B
C b
xa FP=1
FQC
MA
l
FP=1
A
B
RA
1
C
a
b
MC
b
FQC
1
(3) Influence Lines for Overhanging Beams
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a
P=1
L
首先分析几何组 成并绘层叠图。 绘制MK的影响线
1
MK影响线 1
a
0 0
当P=1在CE 段上移动时 EF段上移动时 x 绘制 QB左的影响线 M 影响线与 CE段单独 K CE梁相当于在结 此时 VE 作为一伸臂梁相同。 RF 点 E处受到VE的作用 按上述步骤绘出 QB左 L x段上移动时 当P=1在 AC E VE= 影响线如图。 L MK=0 故MK影响线在EF段为 QB左影响线 返回 直线。
3. 影响线的定义
当一个指向不变的单位集中荷载(通常是竖直向下) 沿结构移动时,表示某一指定量值变化规律的图形,称 为该量值的影响线。 某量值的影响线一经绘出,就可以利用它来确定最不 利荷载位置,应用叠加法求出该量值的最大值。
P=1 A RA
1
1 3/4
P=1 P=1 P P=1
2
1/2
P=1
3
1/4
§11—8 公路标准荷载制 公路上行驶的汽车、拖拉机等类型繁多,载运情况 复杂,设计结构时不可能 对每种情况都进行计算,而是 以一种统一的标准荷载来进行设计。这种标准荷载是经 过统计分析制定出来的,它既概括了当前各类车辆的情 况,又适当考虑了将来的发展。 我国公路桥涵设计使用的标准荷载,分为计算荷载 和验算荷载两种。
例题
a
RB影响线 MK影响线 a
0
K
1
QK影响线(练习)
返回
§11—4 用机动法作单跨静定梁的影响线
静力法和机动法是作影响线的两种基本
方法。 1.机动法的依据—— 虚位移原理 虚位移原理: 即刚体体系在力系作用下处 于平衡的必要和充分条件是:在任何微小的 虚位移中,力系所作的虚功总和等于零。
返回
A 以简支梁为例。 作反力RA的影响线,为 求反力RA,去掉与其相应 的联系即A处的支座,以正 A 1 A 向反力代替。 此时,原结构变成了有 RA 一个自由度的几何可变体 系,给此体系微小虚位移。 令
⊕
QA右影响线
1
⊖
绘制QA右影响线
返回
§11—3 间接荷载作用下的影响线 1.间接荷载(结点荷载)
桥梁结构的纵横梁桥面系统中的主梁受力简图 如图所示。 计算主梁时通常假定纵梁简支在横梁上,横梁 简支在主梁上。荷载直接作用在纵梁上,再通过横 梁传到主梁,即主梁承受结点荷载。这种荷载称为 间接荷载或结点荷载。
1. 一个集中荷载 最不利荷载位置可直观判断。
S影响线 P P
Smax
Smin
返回
2. 可以任意布置的均布荷载(如人群、货物等) 由式 可知
S=q
S影响线
3. 行列荷载 : 一系列间距不变 的移动集中荷载
Smax Smin
但据最不 行列荷载的最不利荷载位置难于直观判定。 利荷载位置的定义可知,当荷载移动到该位置时,所求 量值S最大,因而荷载由该位置不论向左或向右移动到 邻近位置时,S值均将减小。因此,下面从讨论荷载移 返回 动时S的增量入手解决这个问题。
a
b
1
1 回 返
(3)伸臂部分截面内力影响线 D x K d
P=1 P=1
绘制MK、QK影响线 E 当P=1在DK 段上移动时 取K以左为隔离体 MK=-x QK=-1 当P=1在KE 段上移动时
d
1
⊖ ⊖
0
MK影响线 QK影响线
⊖
QA左影响线
1
⊕
取K以左为隔离体 MK=0 QK=0
绘制QA左影响线
1. 问题的提出 工程结构除了承受固定荷载作用外,还要受到移动荷 载的作用。 例如:见图。 在移动荷载作用下,结构的反力 和内力将随着荷载位置的移动而变化,在结构设计中,必 须求出移动荷载作用下反力和内力的最大值。
§11—1 概述
返回
为了解决这个问题,需要研究荷
载移动时反力和内力的变化规律。然
而不同的反力和不同截面的内力变化
B
0 返回
RA的影响线
§11—2 用静力法作单跨静定梁的影响线 1. 绘制影响线的基本方法: 静力法和机动法。 2. 静力法:
将荷载 P=1放在任意位置,并选定一坐标
系,以横坐标 x表示荷载作用点的位置,然后
根据静力平衡条件求出所求量值与荷载位置 x
之间的函数关系,这种关系式称为影响线方程,
再根据方程作出影响线图形。
2. 机动法简介
P=1
B
P
B
A=1
RA=-P
虚功方程为
RAA+PP=0 P RA=- A
此时,虚位移图P便代表了 RA的影响线。 返回
3 .机动法
由前面分析可知,欲作某一反力或内力X的影响线, 只需将与X相应的联系去掉,并使所得体系沿X的正向发 生单位位移,则由此得到的荷载作用点的竖向位移图即 代表 X 的影响线。这种作影响线的方法便称为机动法。 机动法的优点 在于不必经过具体 A 计算就能迅速绘出 影响线的轮廓。 A1
纵梁 P 横梁(结点) 主梁
返回
2. 间接荷载影响线的绘制方法
P=1 P=1 P=1 A C D y E P=1 B
以绘制MC影响线为例
(1)首先,将P=1移动到各 结点处。 其MC与直接荷载作用 在主梁上完全相同。
yD
yE
P=1
x
d
MC影响线
dx d
x d
接荷载作用下MC影响线在D、 E处的竖标为 yD、yE , 在上述 两结点荷载作用下MC值为
例:用机动法绘 MC影响线
C
a
1
P=1
b
B
a A
P
(
B
返回
解:MC(+)+PP=0
令 +=1
AA1= a
MC C M C
§11—5 多跨静定梁的影响线 1. 多跨静定梁影响线绘制步骤 首先分清多跨静定梁的基本部分和附属部分及其传力 关系,再利用单跨静定梁的已知影响线,多跨静定梁的影 2. 举例说明 响线即可绘出。
习题 11—10
8
0
1.5
MC影响线 0 0 3 MK影响线 QC左影响线
1 1
0
0
1
QC右影响线
0
返回
§11—6 桁架的影响线 1. 单跨静定桁架,其支座反力的计算与单跨 静定梁相同,故二者反力影响线相同。
2. 用静力法作桁架内力影响线,其计算方法
与桁架内力的计算方法相同,同样分为结点法和截
面法,不同的是作用的是 P=1的移动荷载,只需求
出P=1在不同位置时内力的影响线方程。
下面以简支桁架为例,说明桁架内力影响线
的绘制方法。
返回
3. 作桁架的影响线
Ⅰ
解:
绘S12影响线 用力矩法,作Ⅰ-Ⅰ 截面。
P=1
Ⅰ
P=1
RA
A
P=1
当 - B 当P=1 P=1在 在2 A - 1间移动时 间移动时 R P=1 B 取左部为隔离体, B 取右部为隔离体, 由∑M5=0 有 由∑ 有 5=0 RM A×3d-S12h=0 R × 5d S12h=0 3d- SB = R 12 A 5h d S12 = RB 1-2)内 当P=1 在节间( h S12影响线 移动时,S12的影响线 为一直线。 返回
第十一章 影响线及其应用
§11—1 概述 §11—2 用静力法作单跨静定梁的影响线 §11—3 间接荷载作用下的影响线 §11—4 用机动法作单跨静定梁的影响线 §11—5 多跨静定梁的影响线 §11—6 桁架的影响线 §11—7 利用影响线求量值 §11—8 铁路和公路的标准荷载制 §11—9 最不利荷载位置 §11—10 换算荷载 §11—11 简支梁的绝对最大弯矩 §11—12简支梁的包络图
计算荷载以汽车车队表示,有汽车—10级、汽车— 15级、汽车—20级和汽车—超20级四个等级(见书上图 11-22)。验算荷载有履带—50、挂车—80、挂车—100 和挂车—120等四种。 返回
§11—9 最不利荷载位置 最不利荷载位置: 使某一量值发生最大(或最小)值的荷载位置,即 为最不利荷载位置。 在移动荷载作用下的结构,各种量值均随荷载位置 的变化而变化,设计时必须求出各种量值的最大值(或 最小值)。为此,要首先确定最不利荷载位置。下面分 几种情况讨论。
2. 分布荷载 将分布荷载沿长度分 每一 成许多无穷小的微段, 微段dx上的荷载为 qxdx, 则ab区段内分布荷载产生的 影响量
qx
qxdx
dx
a
y
b S影响线
q
S= q x ydx (11—3)
a
b
当为均布荷载(q=常数)
a
S= q ydx q
a
b
ω
(11—4)
b
S影响线
返回 式中表示影响线在均布荷载范围内面积的代数和。
P=1
3. 结论
由上可知,多跨静定梁反力及内力影响线的一般作法 如下: (1)当P=1在量值本身梁段上移动时,量值的影响线 与相应单跨静定梁相同。 (2)当P=1在对于量值所在部分来说是基本部分的梁 段上移动时,量值影响线的竖标为零。 (3)当P=1在对于量值所在部分来说是附属部分的梁 段上移动时,量值影响线为直线。 此外,用机动法绘制多跨静定梁的影响线也是很方便 返回 的(课后自行练习)。
ab/L b MC影响线 QC影响线
x=0, MC=0 当 隔离体 ab x=a, MC= L a) QC=-RB (0≤x< 当 P=1在截面C以右移动时, 取截面 以左部分为隔离体 为QC 的左直线。
C
取截面 C以右部分为
-a
L
1
MP=1 a= (a≤x≤L) 当 在 CB段上移动时 , 取截面 C以左部分为隔离体 ab C=RA x=a, MC= L 返回 QC=RA (a<x≤L) (右直线 ) 即M 影响线的右直线。 当
