2 第二讲 应力与应变
最新应力分析与应变分析教学讲义ppt

则有最大剪应力:
max1
3
2
或者: 其中:
且有:
maxmax1{2,23,31}
12122,23223,31321 1223310
§1.2.3 八面体应力与等效应力
即主应力空间的{111}等倾面上的应力。
这组截面的方向余弦为:
度,与塑性变形无关;I3也与塑性变形无关;I2与塑性 变形无关。 7. 应力不变量不随坐标而改变,是点的确定性的判据。
➢ 主应力的求解(略,见彭大暑《金属塑性加工力学》教材) ➢ 主应力的图示
§1.2.2 主剪应力和最大剪应力
➢ 主剪应力(principal shear stress):极值剪应力(不为零) 平面上作用的剪应力。主应力空间的{110}面族。
1MPa=106 N/m2
➢ 应力是某点A的坐标的函数,即受力体内不同点 的应力不同。
➢ 应力是某点A在坐标系中的方向余弦的函数,即 同一点不同方位的截面上的应力是不同的。
➢ 应力的分量表示及正负符号的规定
ij xx 、 xz ……
(便于计算机应用)
i——应力作用面的外法线方向(与应力作用面的外
§1.2 点的应力状态分析
§1.2.1 主应力及应力张量不变量 §1.2.2 主剪应力和最大剪应力 §1.2.3 八面体应力与等效应力
§1.2.1 主应力及应力张量不变量
设想并证明主应力平面(其上只有正应力,剪应力 均为零)的存在,可得应力特征方程:
3I12I2I30 (3I12I2I30)
(1)(2)(3)0
'
'
22
'
'
33
《应力与应变》课件

目录
CONTENTS
• 应力概述 • 应变概述 • 应力与应变的关系 • 应力与应变的应用 • 实验与演示 • 总结与展望
01 应力概述
CHAPTER
定义与概念
定义
应力定义为物体内部单位面积上 所承受的力,用于描述物体受力 状态。
概念
应力是物体受力时内部各部分之 间的相互作用,是物体抵抗变形 和破坏的内在能力。
压缩实验
总结词
通过观察物体在压缩过程中的形变,了解应 力和应变的基本性质。
详细描述
压缩实验是应力与应变研究中另一种重要的 实验方法。在实验中,我们将物体的一端固 定,另一端施加逐渐增大的压力,使物体发 生压缩形变。通过测量压缩量,我们可以计 算出物体的应力和应变。通过观察和记录实 验数据,学生可以了解应力和应变的基本性
应力分类
按作用方式
可分为正应力和剪应力。正应力表示 垂直于受力面的力,剪应力表示与受 力面平行且垂直于切线方向的力。
按作用效果
可分为拉应力和压应力。拉应力表示 使物体拉伸的力,压应力表示使物体 压缩的力。
应力单位与表示方法
单位
应力的单位是帕斯卡(Pa),国际单位制中的基本单位。
表示方法
应力的表示方法通常采用符号“σ”或“σxx”(xx表示方向),例如正应力的 表示符号为σ或σxx,剪应力的表示符号为τ或τxy(xy表示剪切方向)。
进步。
谢谢
THANKS
压缩试验
测定材料的抗压强度、弹性模量等指 标,了解材料在受压状态下的性能表 现。
有限元分析
模型建立
根据实际结构或系统建立有限元 模型,将复杂结构离散化为有限
个单元。
加载与约束
应力与应变关系演示文稿

(D)称为弹性矩阵,将应力与应变的关系写成矩阵形式:
D
第8页,共35页。
各向异性效应
{ } [D]{} 或 {} [ A]{ }
式中:{}为应力列阵;{}为应变列阵;[D] 、[A]为弹性矩阵。
c11c12c13c14c15c16
c21c22
c23c24
c25c26
[D]
c31c32c33c34c35c36
物体的弹性都相同。该平面称为弹性对称面,一般有3个这样的弹性
对称面。
a11a12a13o o o
对于正交各向异性体,由于对称关
a21a22a23o o o
系(正应力分量只产生线应变,不产
a31a32a33o o o
生剪应变)。因此,弹性矩阵中的36 个弹性常数中,有24个为0,在剩下的 12个只有9个是独立的。
x y z yz zx 0
x y z yz zx 0
xy
由广义虎克定律:
xy
G
xy
xy
G
第24页,共35页。
各向同性体的广义虎克定律: (用应力分量表示应变分量)
x
1 E
[
x
( y
z )];
y
1 E
[
y
( z
x )];
z
1 E
[
z
( x
第16页,共35页。
现在来确定各向同性材料独立的弹性常数的个数,设所取的坐标 为三个主轴方向,由广义虎克定律可以得到:
1 C111 C12 2 C133 2 C211 C22 2 C233 3 C311 C32 2 C333
Cij 表示在j轴方向的单位主应变所引起在i轴方向的主应力。
应变和应力关系

新能源技术:利用应变和应力原理,优化风力发电机叶片设计,提高风能 利用率和发电效率。
机器人技术:通过研究应变和应力与机器人关节运动的关系,提高机器人 的灵活性和稳定性,拓展机器人的应用领域。
应变和应力对未来科技发展的影响
增强材料性能:通过深入研究应变和应力,可以开发出性能更强的新型材 料,为未来的科技发展提供物质基础。
智能制造:利用应变和应力的知识,可以优化制造过程中的材料性能,提 高生产效率和产品质量,推动智能制造的发展。
生物医学应用:在生物医学领域,应变和应力的研究有助于更好地理解和 控制人体生理机制,为未来的生物医学应用提供支持。
压痕法:利用压痕仪在物体表面压出一定形状的压痕,通过测量压痕的尺寸来计算应力
应变和应力的相互影响
应变和应力之间的关系:应变是应力作用下的物体形状变化,应力是抵抗变形的力。
应变和应力的测量方法:通过应变计和应力计进行测量,应变计测量物体变形,应力计测量物 体受到的力。
应变和应力的相互影响:应变和应力之间存在相互影响,例如在材料屈服点附近,应变和应力 之间会发生突变。
应力的概念
分类:正应力、剪应力、弯 曲应力等
定义:物体受到外力作用时, 内部产生的反作用力
单位:帕斯卡(Pa) 作用效果:使物体产生形变
应变和应力的关系
应变是物体形状 的改变,应力是 物体内部抵抗变
形的力
应变和应力之间 存在线性关系, 即应变正比于应
力
应变和应力之间 的关系可以用胡 克定律表示,即 应力=弹性模量
应变和应力关系
汇报人:XX
应变和应力的定义 应变和应力的测量方法 应变和应力的应用领域 应变和应力的研究进展 应变和应力的未来展望
02讲-应力与平衡、位移与应变 PPT

刚体位移和变形是同时出现的, 在弹性力学中我们忽略刚体运动对 物体的影响,仅考虑变形。
王正伟
位移的描述 Characterization of Displacement
拉格朗日坐标系其坐标系是放在所描述的物
首先考虑最简单的一维杆在受到轴 向拉伸力时的变形,计算杆中长度 为dx的微元的变化,有
lABAB
xdxuxdxxuxdx
uxdxux
王正伟
应变-位移关系 Strain-Displacement Relationship
对 ux dx 在 x 处Taylor展开有
uxd xuxd d u xd x1 2d d x 2u 2d x2 L
在三维问题中定义正应变相关的方法 与一维杆情况相同,是相对变形长度 与初始长度的比值,为
02讲-应力与平衡、位移与应变
应力与平衡 Theory of Stress and Balance
内力与应力
载荷、内力与应力 斜面应力公式(柯西公式) 主应力 应力莫尔圆
应力平衡微分方程
笛卡儿坐标系下的平衡微分方程 圆柱坐标系下的平衡微分方程
位移与应变
位移与运动的分解 变形的不同描述方式 应变位移的关系
体上随着物体一起运动。 拉格朗日描述法以物体变形前的初始构形为参照构
形,质点变形前的坐标 aa1,a2,a3T 为基本未知
量。将变形后物体的位置 x 表示为 a1, a2 , a3
的函数:x = x (a ),x i x i(a 1 ,a 2 ,a 3 )
u i x i( a 1 ,a 2 ,a 3 ) a i u i( a 1 ,a 2 ,a 3 )
大学物理课件 应力与应变

p gh 1 v2 C
2
pA
1
2
v
2 A
pB
液体流速为
vA
2( pB pA )
2gh
h h
AB
pA p0 gh1 A pB p0 gh2 p pB pA gh
(2)测气体的流速 (设 为液体密度, 为气体密度)
p gh 1 v2 C
2
vA 0, vB v
关于 A、A' 点:
pA
pA'
1 2
v
2 A'
关于 B、B' 点:
pB
1 2
vB2
'
hB 0 ghB pB
'
1 2
vB2 '
pB
1 2
vB2
pA'
1 2
v
2 A'
pA
气体流速为
B'
vB
2( pA pB )
A'
pA pB gh
vB
2gh
h h
AB
3. 文特利流量计原理 中间细,两端粗的一段短管,串接于欲测管道中.
f
f´
速度梯度 lim v d v y0 y d y
v =0 B x y
粘滞定律 f dv S dv
f
dy
d y y
f
v2 v1
黏滞系数与流体本身性质有关。
液体
O
z
x
温度
主要取决于分子吸引力
气体
主要取决于不规则运动的动量交换
二、实际流体稳定流动的伯努利方程
p1
p
gh1
gh 1 v2 C
应力与应变弹性 - 应力与应变、弹性

较小的应力和较短的时间里,木材的性能十 分接近于弹性材料;反之,近似于黏弹性材料。
8.1 应力与应变
(3) 刚度、脆性、韧性和塑性
① 刚度
物体受外力作用时保持
其原来形状和大小的能力。
➢ 木材具有较高刚度(密度比) 适用于建筑材料。
应县木塔
➢我国现存最古老、最高大 的纯木结构,楼阁式建筑。
应力-应变曲线 ➢ 破坏点:M ➢ 破坏应力:σM ➢ 破坏应变:εM ➢ 屈服点:F ➢ 屈服应力:σY
应力
应力
σ
σM
PE D
M
σP
O εP 应变 εM ε σ
σY
F
G
O
应变
ε
应力-应变曲线(模式图)
讨论:
木材应力与应变之间的关系?木材 属于什么性质的材料?
8.1 应力与应变
(2) 应力与应变的关系
ΔL
正应变示意图
8.1 应力与应变
(2) 应力与应变的关系
应力-应变曲线 ➢ 比例极限应力:σP ➢ 比例极限应变:εP ➢ 弹性极限:σP-E ➢ 弹性应变:<εE ➢ 塑性应变:>εE
应力
σ
M
σM σP
E P
D
O
εP 应变
ε εM
应力-应变曲线(模式图)
8.1 应力与应变
(2) 应力与应变的关系
σM σP
E P
D
M
应力
O
εP 应变 εM ε
8.1 应力与应变
(1) 应力与应变的概念
① 应力(Stress)
P
P
物体在外力作用下单位面
积上的内力。
材料力学基础

材料力学基础材料力学是研究材料在外力作用下的变形、破坏和性能的一门学科。
它是材料科学的重要组成部分,对于材料的设计、制备和应用具有重要的指导意义。
本文将介绍材料力学的基础知识,包括应力、应变、弹性模量、屈服强度等内容。
首先,我们来介绍应力和应变的概念。
应力是单位面积上的力,通常用σ表示,其计算公式为F/A,其中F为受力,A为受力面积。
应变是物体长度相对于初始长度的变化量,通常用ε表示,其计算公式为ΔL/L,其中ΔL为长度变化量,L为初始长度。
应力和应变是描述材料在外力作用下的变形情况的重要物理量。
接下来,我们将介绍材料的弹性模量。
弹性模量是描述材料抵抗变形的能力的物理量,通常用E表示。
对于线弹性材料,弹性模量可以通过应力-应变关系来计算,即E=σ/ε。
弹性模量是衡量材料刚度和变形能力的重要参数,不同材料的弹性模量具有很大差异,对于材料的选择和设计具有重要意义。
除了弹性模量,材料的屈服强度也是一个重要的力学性能参数。
屈服强度是材料在受力过程中开始发生塑性变形的应力值,通常用σy表示。
当材料受到的应力超过屈服强度时,材料会发生塑性变形,这对于材料的加工和使用具有重要的影响。
屈服强度是衡量材料抗拉伸能力的重要指标,对于材料的工程应用具有重要意义。
此外,材料的断裂行为也是材料力学研究的重要内容。
材料的断裂行为通常可以通过拉伸试验来研究,通过拉伸试验可以得到材料的断裂应力和断裂应变。
断裂应力和断裂应变是描述材料断裂性能的重要参数,对于材料的设计和评价具有重要意义。
综上所述,材料力学是研究材料在外力作用下的变形、破坏和性能的重要学科,其基础知识包括应力、应变、弹性模量、屈服强度等内容。
这些基础知识对于材料的设计、制备和应用具有重要的指导意义,是材料科学不可或缺的重要组成部分。
希望本文的介绍能够对读者对材料力学有所了解,并对材料科学的学习和研究有所帮助。
2 第二章 应力和应变_wan

第二章 应力和应变地震波传播的任何定量的描述,都要求其能表述固体介质的内力和变形的特征。
现在我们对后面几章所需要的应力、应变理论的有关部分作简要的复习。
虽然我们把这章作为独立的分析,但不对许多方程进行推导,读者想进一步了解其细节,可查阅连续介质力学的教科书。
三维介质的变形称为应变,介质不同部分之间的内力称为应力。
应力和应变不是独立存在的,它们通过描述弹性固体性质的本构关系相联系。
2.1 应力的表述——应力张量 2.1.1应力表示考虑一个在静力平衡状态下,均匀弹性介质里一个任意取向的无限小平面。
平面的取向可以用这个平面的单位法向矢量nˆ来规定。
在n ˆ方 向的一侧施加在此面单位面积上的力叫做牵引力,用矢量),,()ˆ(z y x t t t nt =表示。
在n ˆ相反方向的另一侧施加在此面上的力与其大小相等,方向相反,即)ˆ()ˆ(n t nt -=-。
t 在垂直于平面方向的分量叫做法应力,平行于平面方向的分量叫做剪应力。
在流体的情况下,没有剪应力,n p t ˆ-=,这里P 是压强。
在笛卡尔坐标系(图 2.1)里,应力张量τ可以用作用于xy xz yz ,,平面的牵引力来定义+:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=zz zy zx yz yy yx xz xy xx z z z z y y x x x z t y t x t z t y t xt z t y t x t ττττττττττ)ˆ()ˆ()ˆ()ˆ()ˆ()ˆ()ˆ()ˆ()ˆ( (2.1)应力分量的符号规定如下:对于正应力,我们规定拉应力为正,压应力为负。
对于剪应力,如果截面的外法线方向与坐标轴一致,则沿着坐标轴的正方向为正,反之为负;如果截面方向与外法线方向相反,则沿着坐标轴反方向为正。
图 2.1 在笛卡尔坐标系里描述作用在无限小立方体面上的力的牵引力矢量)ˆ(),ˆ(),ˆ(z t y t xt 。
+通常,应力张量用脚标互换的(2.1)式来定义,第一个脚标表示面的法向方向。
应变和应力的关系公式

应变和应力的关系公式应变和应力是力学中非常重要的概念,它们描述了物体在外力作用下的变形和反抗变形的能力。
应变是物体在外力作用下发生变形的程度,而应力是物体对外力的反抗程度。
应变和应力之间存在着一定的关系,下面将通过分析和解释来阐述这一关系。
我们来看一下应变的定义。
应变通常用来描述物体的形变程度。
当物体受到外力作用时,它的形状会发生改变,这种形变程度就是应变。
应变可以分为线性应变和非线性应变。
线性应变是指物体的形变与受力成正比,比如拉伸或压缩后物体的长度或体积的变化。
非线性应变则是指物体的形变与受力不成正比,比如物体的弯曲或扭转。
而应力则是物体对外力的反抗程度。
当物体受到外力作用时,它会产生内部的应力,以抵抗外力的作用。
应力可以分为正应力和剪应力。
正应力是指物体内部的应力沿着受力方向的成分,比如拉伸或压缩时物体内部的张力或压力。
剪应力则是指物体内部的应力与受力方向垂直的成分,比如物体发生弯曲或扭转时的切向应力。
应变和应力之间的关系可以通过胡克定律来描述。
胡克定律是力学中一个重要的定律,它描述了弹性体的应力和应变之间的线性关系。
根据胡克定律,当外力作用于弹性体时,弹性体产生的应变与外力成正比,且比例常数为弹性模量。
弹性模量是描述物体抵抗形变能力的物理量,通常用符号E表示。
胡克定律的数学表达式为:应力=弹性模量×应变。
这个关系可以简洁地表示了应变和应力之间的关系。
根据这个关系,我们可以推导出应变和应力之间的其他关系。
比如,如果已知应变和弹性模量,可以通过应变乘以弹性模量来计算应力。
同样地,如果已知应力和弹性模量,可以通过应力除以弹性模量来计算应变。
除了胡克定律,还有其他的应变与应力之间的关系,比如柯西应变与柯西应力之间的关系、拉梅应变与拉梅应力之间的关系等。
这些关系都是通过实验和理论推导得到的,它们描述了不同应变与应力之间的关系,适用于不同的物体和力学问题。
总结起来,应变和应力之间存在着一定的关系,可以通过胡克定律或其他相关定律来描述。
应力与应变间的关系
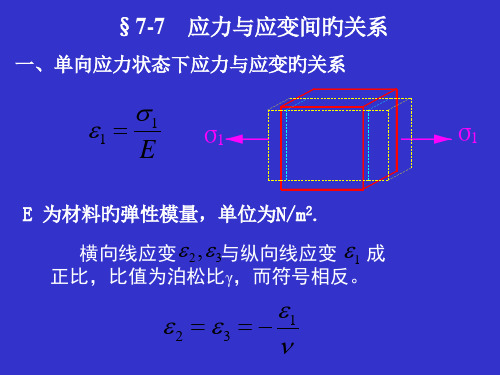
一、单向应力状态下应力与应变旳关系
1
1
E
σ1
σ1
E 为材料旳弹性模量,单位为N/m2.
横向线应变2,3与纵向线应变 1 成
正比,比值为泊松比γ,而符号相反。
2
3
1
二、纯剪切应力状态下应力与应变旳关系
G 或
G
τ γ γτ
G 为剪切弹性模量,单位为N/m2.
三、复杂应力状态下应力与应变旳关系
x y z x y y z z x
y
σy
上面
x y z x y y z z x
1、各向同性材料旳广义胡克定律 (1)符号要求
τ yx
τ τ yz
xy
τ τ zy xz
τ zx
右侧面
σx
(a)三个正应力分量:拉应力为正
σz
x
o
压应力为负。 z
前面
(b)三个剪应力分量: 若正面(外法线与坐标轴
P a
y
z
x
y 解:铜块上截面上旳压应力为
y
P A
300 103 0.12
y x
30MPa
x
(b) Z z
1 [ ( )] 0
xE x
y
z
由
1 [ ( )] 0
zE z
x
y
解得
x
z
(1 1 2
)
y
0.34(1 0.34) 1- 0.342
(30)
-15.5MPa
特例
在平面纯剪切应力状态下:σ 1 σ 3 τ xy
代入得
1 2
E
(1
2
3)
1 2
2应力与应变091

2.2 体力和面力
为了表明物体在xyz 坐标系 内任意一点P 所受体力的大小和 方向,在P点的邻域取一微小体 积元素△V, 如图所示 。设△V 的 体力合力为△F,则P点的体力平 均集度为:
∆F = Fb ∆V
令微小体积元素△V 趋近于0,则可以 定义一点P的体力为 :
∆F lim = Fb ∆V → 0 ∆V
∆F pn = ∆S
∆F pn = lim ∆S → 0 ∆S
[ 力 ][ 长 度 ] -2
2.2 体力和面力
正应力σ: 正应力 :应力在其作用截面的法线方 向的分量,称正应力。 向的分量,称正应力。 切应力τ 切应力τ:应力在其作用截面的切线方 向的分量,称切应力。 向的分量,称切应力。
弹性体的强度与正应力和切应力息息相关, 弹性体的强度与正应力和切应力息息相关,因 此这是工程结构分析式经常使用的应力分解形 式。 的方向只有一个, 由于微分面法线 n 的方向只有一个,因此说明 的方向。 截面方位就确定了正应力 σn的方向。但是平行 于微分面的方向有无穷多,因此切应力τ 于微分面的方向有无穷多,因此切应力τn不仅 需要确定截面方位,还必须指明方向。 需要确定截面方位,还必须指明方向。
10
2.2 体力和面力
为表达物体内部任意一点 的应力状态, 为表达物体内部任意一点M 的应力状态,利用三个与坐标轴 一点 方向一致的微分面,通过M点截取一个微小的正平行六面体 点截取一个微小 方向一致的微分面,通过 点截取一个微小的正平行六面体 单元
2.2 2.2 体力与面力
正面:外法线沿着坐标轴的正方向的截面 截面。 正面:外法线沿着坐标轴的正方向的截面。
t x σ x τ xy τ xz λx t = τ σ y τ yz λ y y xy t z τ xz τ yz σ z λz
应力与应变分析课件

03
边界元法
边界元法是一种基于边界积分方程的数值方法,适用于解决各种物理问
Байду номын сангаас
题。未来,边界元法将在更多领域得到应用,例如流体力学、电磁场等
问题。
考虑材料非线性的影响
材料非线性是指材料的应力-应变关系不是线性的,需要考虑 材料内部结构、相变等因素的影响。未来,研究人员将进一 步考虑材料非线性的影响,以更准确地预测材料的力学性能 。
解方程
通过加权残值法,求解方程中 的参数,使得残值的平方和最
小化。
05
应力与应变分析在工 程中的应用
结构优化设计
总结词
提高结构性能与稳定性
详细描述
应力与应变分析在结构优化设计中具有重要作用,通过分析可以评估结构的强 度、刚度和稳定性,发现潜在的薄弱环节,为结构设计和改进提供依据,从而 提高结构的性能与稳定性。
应力分类
根据作用力的来源和性质,应力 可以分为多种类型,如正应力、 剪应力、弯曲应力等。
应力与应变的关系
应力的作用
应力作用在物体上,会导致物体 内部发生形变,即应变。
应变分类
应变分为线应变和角应变,分别表 示物体形状和大小的改变。
弹性力学基本方程
描述应力与应变之间关系的方程, 如胡克定律(Hooke's law)。
应力应变关系。
04
应变分析的基本方法
直接方法
定义应变分量
根据物体的形状和受力情况,将物体分为多个小的单元,并定义 每个单元的应变分量。
建立方程
根据弹性力学方程和应变分量的定义,建立物体整体的应变方程。
解方程
根据方程的解,得到每个点的应变值。
最小二乘法
确定目标函数
应力和应变

应力和应变1. 简介在力学和材料科学中,应力和应变是两个重要的概念。
应力是指材料内部受到的力的作用,而应变是指材料在受到力作用后发生的形变。
应力和应变是描述材料力学性能的基本参数,对于材料的设计和工程应用具有重要意义。
2. 应力应力是材料内部受到的力的作用,通常用符号σ表示,其单位是帕斯卡(Pa),也可以使用兆帕(MPa)或千兆帕(GPa)。
应力可以分为三类:正应力、剪应力和法向应力。
2.1 正应力正应力是指作用在材料内部的垂直于截面的力,可以通过力除以截面积来计算。
正应力可以进一步分为拉应力和压应力,分别表示拉伸和压缩材料时的应力。
拉应力表示材料受到拉伸作用时的应力,通常以正数表示。
拉应力会使材料发生形变,具有延展性和弹性,可以恢复原状。
压应力表示材料受到压缩作用时的应力,通常以负数表示。
压应力会使材料发生形变,具有收缩性和塑性,并且不易恢复原状。
2.2 剪应力剪应力是指作用在材料内部的平行于截面但方向不同的力,可以通过力除以截面积来计算。
剪应力会使材料发生扭转和剪切形变。
剪应力会产生剪切变形,对应的是材料的剪切模量,可以用于描述材料的硬度和可塑性。
2.3 法向应力法向应力是指作用在材料内部的垂直于截面方向的力,可以通过力除以截面积来计算。
法向应力会使材料发生压缩或拉伸形变。
法向应力的大小和方向取决于施加力的方向和大小,可用于描述材料的稳定性和破坏性。
3. 应变应变是材料在受到力作用后发生的形变,通常用符号ε表示。
应变可以分为线性应变和非线性应变两类。
3.1 线性应变线性应变是指材料在受到小应力作用时,形变与力之间的关系是线性的。
线性应变可以通过材料的弹性模量来描述,弹性模量是材料在小应力作用下恢复原状能力的度量。
3.2 非线性应变非线性应变是指材料在受到大应力作用时,形变与力之间的关系是非线性的。
非线性应变通常发生在超过材料弹性极限时,即材料开始变形并难以恢复原状的阶段。
非线性应变可以引起材料的塑性变形和破坏,对于材料的设计和使用具有重要影响。
§2 应力应变分析及应力应变关系23

2 sin 2 x cos 2 0
主方向公式
2 x tan2 P x y
P 2 P1 90 - ~内,得两个值 P1 和 P 2 ,且
即这两个主平面相互垂直
13
主平面上的正应力称为主应力
将P1,P2代入(2.12)得出主平面上的主应力为:
例如外力作用在板平面内的薄板内任意点 取出的单元体
9
1.平面应力状态的工程表示方法 应力分量的正负号规定: y 正应力 x , y 以拉为正 y 切应力 x , y 以使单元体顺
y
x
x
时针转动为正
x
y
x
y
x
故切应力互等定理为:
x y
2. 斜截面应力公式——解析法
y
x
y x
x
y
x
y
2
x
上两式两边平方后相加
x y
2
2
2
x y 2
,
2
x y
2
R
2
2
圆的方程:圆心 ( 圆的半径: R
(
x y
§2 应力应变分析及应力应变关系
§2.1 应力的概念 一点处的应力状态
1. 应力的概念
用截面法求某一截面上的内力,得出该截面上的 内力分量:FN , FS , T , M ——截面分布内力系向截 面形心简化后的等效力系 y x F
R
FN
T
FS
z
MC
为正确描述变形,应在 该截面上的每一点,描 述内力的状况。
x y x y 2 主应力公式 (2.15) x 2 2 x y x y cos2 x sin 2 由斜面应力公式 2 2 x y d 2 sin 2 2 x cos 2 0 令 d 2
应力应变概念

U(ro+ )=U(ro)+(dU/dr)ro +1/2(d2U/dr2) ro 2 =U(ro)+1/2(d2U/dr2)ro 2
F=du(r)/dr=(d2U/dr2)ro K =(d2U/dr2)ro就是势能曲线在最小值u(ro)处的曲率。
结论:弹性常数的大小实质上反映了原子间势能曲线 极小值尖峭度的大小。
化),则 :
K=m(2)2=m(2c/)2
可以利用晶体的红外吸收波长测出弹性常数。
3. 影响弹性模量的因素
(1)晶体结构
架状结构 石英和石英玻璃的
架状结构是三维空间网络,不同方 向上的键结合几乎相同------几乎各 向同性。
单链结构
Si2O6
双链结构
Si4O11
环状结构(岛状结构) Si6O18
(2) 温度
大部分固体,受热后渐渐开始变软,弹性常数随温度 升高而降低。
弹性模量与温度的定量关系: E=Eo-bTexp(-To/T)
或
(E-Eo)/T=-bexp(-To/T)
Eo,b,To是经验常数,对MgO,Al2O3,ThO2等氧化物, b=2.7~5.6 , To=180~320
温度对弹性刚度系数的影响,通常用弹性刚度系数的温 度系数表示: Tc=(dC/dT)/C
•
•
•
•
说明:Tc和转动相关。
启示:温度补偿材料具有敞旷结构,内部结构单位能 发生较大转动的物质,这种敞旷式结构具有小的配位 数。
架状结构:方石英、长石、沸石、白榴子石等具有正 的Tc.
(3)复相的弹性模量
对于剪切应变,则有如下虎克定律:
xy=xy/G yz=yz/G zx=zx/G G ------剪切模量或刚性模量。 G, E, 参数的关系: G=E/2(1+) 如果 x = y = z ,材料的体积模量K------各向同等 的压力与其引起的体积变化率之比。 K=-p/(V/V)=E/[3(1-2 )]
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Y
• 应变椭球体的圆切面 为无伸缩面。 • 无伸缩面与3之间为 挤压应变区,岩石遭 受到挤压变形; • 无伸缩面与1之间为 拉伸应变区,岩石遭 受到拉伸变形。
X
Y Z
三个主应变面:XZ面;XY面;YZ面
2. 旋转应变与非旋转应变
根据应变主轴方向的物质线在变形前后平行与否,可把应变分为旋 转应变与非旋转应变。 非旋转变形又称无旋转变形, 1和3质点线方向在变形前后保持不变。 如果体积不变而且2=0,则称为纯剪应变。 旋转应变的1和3质 点线方向将会改变。 最典型的情况是单 剪应变,是由物质 中质点沿着彼此平 行的方向相对滑动 而成。
变形。
• 变形前的直线在变形后仍是直线; • 变形前的平行线在变形后仍然平行。 • 其中的单位圆变形后成为椭圆,称为应变椭 圆 • 其中任何一小单元的应变性质(大小和方向) 可以代表整个物体的变形特征。
均匀变形
非均匀变形:物体内各点的应变特征随其 位置而发生变化的变形。
非均匀变形
• 连续变形: • 物体内从一点到另一 点的应变状态是逐渐 改变的。 • 不连续变形: • 如断裂。
Carrara大理岩在不同围 压下变形差异应力-应变 曲线
拉伸和挤压实验中脆-韧性 过度与温压的关系
2.温度
温度是影响岩石强度和变形行为的一个重要因素。 温度升高降低岩石强度,岩石变形由脆性转变为韧 性。 引起热蠕变,当温度达到500℃岩石蠕变强度变的极 低(0.1~1MPa)。热蠕变对解释深部构造层次变质岩 中各种复杂的应变具有特殊的意义。
图解中P点的K值代表任意一点的应变椭 球体状态,P点与坐标原点(1,1)之间 的距离d反映了应变椭球体的应变强度。 当e2 = 0, K = 1, V = 0时,称为平 面应变; 当e2 0时,为压扁应变区; 当e2 0时,为收缩应变区。
四、均匀变形和非均匀变形 • 物体内各点的应变状态相同的变形称均匀
。
递进变形就是许多次无限小应变逐渐累积 的过程。在变形史的任一阶段,都可把应变 状态分解为两部分:一部分是已经发生了的 有限应变;另一部分是正在发生的无限小应 变或增量应变。
2. 共轴递进变形与非共轴递进变形 在递进变形过程中,如果各增量应变椭球 的主轴始终与有限应变椭球的主轴一致,这种 变形叫共轴递进变形。否则就叫非共轴递进变 形。
在上述四个带中强硬岩层形成如下构造:
• 1带:已经形成的石香肠正被挤压在一起或形成 褶皱; • 2带:已经形成的石香肠,继续被拉伸增大间距。 • 3带:已经形成褶皱遭受到拉伸,褶皱展开或石 香肠化破坏; • 4带:已经形成褶皱遭受到继续压缩,褶皱波长 减少,波幅增大;
依据有限应变椭圆主轴方位与无限小应变椭圆主轴方位是否 发生变化,可以划分为共轴递进变形和非共轴递进变形
2)作为溶剂,促进物资的溶解和运移,改变岩石的成 分和结构使得岩石易于变形;
3)润滑作用,降低颗粒之间的粘结力,易于产生滑动。 最为典型的实例是逆冲推覆构造;
e0 e 或e0 e
l0 l
泊松效应
杆件的简单拉伸变形
b0
b
线应变 构造现 象实例
L0 3. 剪应变 变形前相互垂直 的两条物质线,变形 后其夹角偏离直角的 改变量称为角剪应变 ,其正切称为剪应 变 =tg
L1
L
• 即:
=tan ( 3) 并约定:顺时针方向旋转的剪应变 为正值、逆时针方向旋转的剪应变为负 值。
构造解析 第二讲 应力与应变分析
Structural Geology: Deformation of Rocks
刘正宏
• 内容提要:
• 一、变形、位移和应变的概念
• 二、应变与应变类型
• 三、应变椭球体 • 四、均匀变形和非均匀变形 • 五、岩石的变形阶段 • 六、影响岩石和矿物变形的因素
一、变形、位移和应变的概念 1. 变形 处于地壳和岩石圈中的任何地质体,受 到力作用而会发生变形。 变形是指地质体(物体)初始形状、方 位或位置发生了改变。
伸展盆地的两种动 力学模型
a. b. 纯剪切模型 (Mckenzie模型); 简单剪切模型 (Wernicke模型)
纯剪盆地从形态上看是对称的,下地壳和上地幔中没有剪切 滑脱面。而简单剪切伸展模式则以一条穿透上地幔或下地壳 的滑脱面为特征,盆地的构造形态不对称,软流物质的上涌 不像纯剪模式那样位于盆地的正下方,而是偏移到了盆地的 一侧。
4.同构造脉的形成机制与递进变形
• 作为伸展方向标志的张裂隙 • 裂隙方向的变化指示增量应变 方向的变化 • 当增量应变方向改变时: • 1)沿早期裂隙末端改变方向 • 2)早期裂隙的斜向张开 • 3)新生裂隙切过早期裂隙
A-最早形成的裂隙垂直于最大增量线应变方向,而裂隙两壁的分离垂直两壁 (a-a’),如果后继的增量方向不与早期增量方向一致,则会出现三种几何特 征,一、末端将侧向扩展,其方向受后来的应变增量轴控制;二、横过早期 的裂隙扩张继续加大,新的扩张方向平行新的增量的最大应变方向;三、张 开裂隙之间的块体显示出旋转的趋势。
C A O B D d 56 20'
简单剪切 (单剪) a
40 O' b c A O'
c
33 40'
刚体旋转=
=22 40'
纯剪
b
单剪与纯剪应变
2
1
1
2
变形体力学中定义的纯剪切和简单剪切
纯剪切的力学条件是:1=-2,张应力与压应力大小相等,符号相反, 在与主应力呈45º 夹角的斜截面上,仅作用有纯粹的剪切应力,因而 称为纯剪切。 如果从与边界上剪切力方向相平行的截面上仅作用有剪应力的意义上来 说,纯剪切与简单剪切并无实质上的区别。
根据材料在破裂前 塑性变形的应变量 可以把材料分为脆 性材料(<5%)、 韧性材料(>10%)、 韧-脆性材料(5~ 7.5%)和脆-韧性 材料(7.5~10%)。
弹性变形区
y' y
塑性变形区
P
破裂
e1
e2
e
岩石变形的 一般化应力-应变曲线
六、影响岩石和矿物变形的因素
• • • • 外部因素(围压、温度、应变速率、流体); 内部因素(成分、结构等) 1.围压 围压增高会提高岩石强度,当围压达到一定 程度时,岩石变形行为也由脆性转变为韧性。
三、应变椭球体 1. 概念 单位圆球体经均匀应变变成的椭球体 称为应变椭球体
X 应变椭球体内有三个互相垂 直的主轴,沿主轴方向只有 线应变而没有剪应变,称之 为应变主轴。分别以1,2, 3(或X, Y, Z)表示。椭球 体的三个主轴的半径分别为 √1,√2,√3。 包含应变椭球体的任意两个 Z 主轴的平面叫做应变主平面。
拉伸
挤压
中和面
剪切
弯曲
扭转
• 2. 位移 位移是指地质体(物体)及其内部各 质点初始位置的改变,是通过物体内各质 点的初始位置和终止位置的变化来表达的。 质点的初始位置和终止位置的连线叫 位移矢量。这条线只代表位移的最终结果, 而不代表位移的实际路径。
• 3. 位移方式
平移 四种: • 平移-变形前后质 P 点位置的平行移 动; • 旋转-变形前后物 ( 虚线为可能的路径) 质线方位的改变; • 形变-变形前后物 P 体形状的改变; P 体变-变形前后物 体体积的改变
l3 l2
l1
缩短量0% 20% 30% 40% 50% 0 20 30 40 50 l1 的变形史
(%)
l3 的变形史
l2的变形史
共轴递进变形
3. 递进变形过程中线的长度变化及其地质意义
• (一)增量应变椭圆i叠 加在有限应变椭圆f上的 几何关系 • 1带:有限应变线已经 伸长,无限小应变正受 到挤压; • 2带:有限应变线已经 伸长,无限小应变时继 续受到拉伸; • 3带:有限应变线已经 缩短,无限小应变正受 到拉伸; • 4带:有限应变线已经 伸长,无限小应变继续 缩短;
纤维晶体自两 壁向中心生长, 相向生长的晶 体于中心遇合, 形成一条锯齿 状中线;纤维 晶体成分与两 侧物质相同; 纤维晶体方向 变化受增量应 变控制。
反向脉是自 中心向两壁 生长,常在 中心形成包 体带;脉体 成分与两侧 岩石成分有 有教大差别;
晶体与脉壁 上岩石成分 相似,拉长 是晶体从一 壁到另一壁 结晶上连续 的链
3. 应变椭球的意义 1代表最大延 伸方向(物质 运动方向), 平行于构造岩 中的拉伸线理 方向;擦痕方 向
(2) (1) (3)
X
Z Y
X
Z Y
• 与1垂直的面为一个张性面(YZ 面),是张节理发育的方向。
X
Z Y
• 与3 垂直的面(XY面)是一个挤压面, 包括褶皱面。
X
XY面
a-a’曾彼此接触, 在递进变形过程中 分开,二者之间的 距离表示一个局部 位移矢量。
递进张开的张裂隙的几何特征和同构造形成的纤维脉的形状
5. 同构造脉的充填
为什么石英、方解石、绿泥石等 成纤维状结晶? 与晶洞中自形晶体之差别。 区别和特点在于: 1)非常细长的形态,有极大的 长宽比值; 2)纤维的长度相对构造纤维晶 体的结晶方位没有特定的方向; 3)纤维的结晶方向可以直接继 承脉壁岩石中的结晶方向; 4)纤维脉可以是直的,也可以 是弯曲的,但结晶方向是稳定的
Z Y
大多数劈理代表挤压面
(2)
(1)
(3)
4. 应变椭球体的类型:Flinn 图解 应变椭球体的形态及其类型可用图解 来表示,其中Flinn 图解是常用的。在该图 解中: a = X / Y = ( 1 + e1 ) / ( 1 + e2 ) ( 4) b = Y / Z = ( 1 + e2 ) / ( 1 + e3 ) ( 5) K = tan = ( a-1) / ( b-1) (6)
