4.3 向量的平行和垂直(无附答案)人教版
2019-2020学年高中数学课时作业空间向量与平行垂直关系新人教A版选修

设平面SCD的法向量为n=(1.y.z).
则n· =(1.y.z)·(1,2,0)=1+2y=0.∴y=- .
又n· =(1.y.z)·(-1,0,2)=-1+2z=0.∴z= .
∴n= 即为平面SCD的一个法向量.
10.如图所示.在直三棱柱ABC-A1B1C1中.∠ABC=90°.BC=1=4.EB1=1.D.F.G分别为CC1.B1C1.A1C1的中点.
由题意知SO⊥平面ABCD.
以O为坐标原点.
. . 分别为x轴.y轴.z轴正方向.建立空间直角坐标系如图.
设底面边长为a.则高SO= a.
于是S .D .B .C .
= .
= .
则 · =0.
故OC⊥SD.从而AC⊥SD.
(2)棱SC上存在一点E使BE∥平面PAC.
理由如下:
由已知条件知 是平面PAC的一个法向量.
解析:由l1⊥l2知.a·b=0.即1×(-2)+2×3+(-2)×m=0.解得m=2.
答案:2
7.若A .B .C 是平面α内三点.设平面α的法向量为a=(x.y.z).则x∶y∶z=________.
解析: = . = .
由
得 解得
则x∶y∶z= y∶y∶ =2∶3∶(-4).
答案:2∶3∶(-4)
8.已知点P是平行四边形ABCD所在的平面外一点.如果 =(2.-1.-4). =(4,2,0). =(-1,2.-1).对于结论:①AP⊥AB;②AP⊥AD;③ 是平面ABCD的法向量;④ ∥ .其中正确的是________(填序号).
解析:由于 · =-1×2+(-1)×2+(-4)×(-1)=0. · =4×(-1)+2×2+0×(-1)=0.
人教版四年级上册数学平行与垂直课件PPT

点击添加相关标题文字,点击添加相关标题文字,点击添加相关标题文字,点击添加相关标题文字,点击添加相关标题文字。
教学过程
单击此处添加文本
单击此处添加文本
单击此处添加文本
单击添加标题
单击添加标题
三、课堂小结
在同一平面内,两条直线的位置关系有相交和不相交,不相交的两条直线叫做平行线,也可以说这两条直线互相平行。 相交的两条直线的关系有垂直和不垂直,如果两条直线互相垂直,其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足。
四、拓展训练
选一选。 1.在同一平面内的两条直线,一定是( )。 A、相交的 B、平行的 C、不相交就平行 2.两条直线相交,如果其中一个角是直角,那么这两条直线( )。 A、互相垂直 B、互相平行 C、无法确定 3.在同一平面内,有两条直线都与同一条直线平行,这两条直线( )。 A、互相垂直 B、互相平行 C、相交 4.长方形相邻的两条边( ),相对的两条边( )。 A、互相平行 B、互相垂直 C、没有关系
教学反思
感谢聆听
演讲人:
2019
点击输入详细文本内容,点击输入详细的文本内容,点击输入详细的文本内容。
2020
点击输入详细文本内容,点击输入详细的文本内容,点击输入详细的文本内容。
教学策略
添加 标题
添加标题内容 您的内容打在这里,或者通过复制您的文本后,在此框中选择粘贴,并选择只保留文字。您的内容打在这里,或者通过复制您的文本后,在此框中选择粘贴,并选择只保留文字。 您的内容打在这里,或者通过复制您的文本后,在此框中选择粘贴,并选择只保留文字。您的内容打在这里,或者通过复制您的文本后,在此框中选择粘贴,并选择只保留文字。
2024版高考数学总复习:立体几何中的向量方法__证明平行与垂直课件

为n,m
α⊥β
n·m=0
n⊥m⇔________
二、基本技能·思想·活动经验
1.判断下列说法的正误,对的画“√”,错的画“×”.
(1)直线的方向向量是唯一确定的.
( × )
(2)平面的单位法向量是唯一确定的.
( ×)
(3)若两平面的法向量平行,则两平面平行.
( √ )
(4)若两直线的方向向量不平行,则两直线不平行.
( √ )
(5)若a∥b,则a所在直线与b所在直线平行.
( × )
(6)若空间向量a平行于平面α,则a所在直线与平面α平行.
( × )
1
2
3
4
5
2.若直线l的方向向量a=(1,-3,5),平面α的法向量n=(-1,3,
-5),则有(
)
A.l∥α
B.l⊥α
C.l与α斜交
D.l⊂α或l∥α
B
解析:由a=-n知,n∥a,则有l⊥α.故选B.
第六章
第六节
立体几何
立体几何中的向量方法—
—证明平行与垂直
考试要求:1.理解直线的方向向量及平面的法向量,能用向量语言
表述线线、线面、面面的平行和垂直关系.
2.能用向量方法证明立体几何中有关直线、平面位置
关系的判定定理.
01
必备知识·回顾教材重“四基”
一、教材概念·结论·性质重现
1.直线的方向向量与平面的法向量
2.空间位置关系的向量表示
位置关系
向量表示
直线l1,l2的方向向量分
l1∥l2
n1∥n2⇔n1=λn2
别为n1,n2
l1⊥l2
n1·n2=0
n1⊥n2⇔__________
向量平行公式和垂直公式

向量平行公式和垂直公式向量是数学中的一个重要概念,广泛应用于几何学、物理学和工程学等领域。
在向量运算中,判断向量是否平行或垂直是一项基础的操作。
本文将详细介绍向量的平行公式和垂直公式,并通过数学推导和几何解释来说明其原理和应用。
一、向量的定义和表示法向量是带有方向的量,可以用有序的两个点来表示。
通常使用箭头表示,箭头的起点表示向量的起点,箭头的方向表示向量的方向,箭头的长度表示向量的大小。
在笛卡尔坐标系中,向量通常用坐标表示,例如向量a可以表示为:a=(x,y)其中,x表示向量在x轴方向上的分量,y表示向量在y轴方向上的分量。
二、向量的平行概念两个向量a和b平行的概念是指它们的方向相同或相反。
具体来说,如果存在一个实数k,使得向量a与向量b的每个对应分量满足以下关系:a=k*b其中,k表示两个向量的比例因子。
如果k为正数,则表示两个向量的方向相同;如果k为负数,则表示两个向量的方向相反。
三、向量的平行判断公式根据向量的平行定义,可以推导出判断两个向量平行的方法。
假设有两个向量a=(x1,y1)和b=(x2,y2),向量a与b平行的条件可以表示为:x1/x2=y1/y2这个条件说明,两个向量的x轴分量和y轴分量的比例相等时,它们是平行的。
从几何上来看,这表示两个向量在坐标平面上的斜率相等,即它们的直线方程具有相同的斜率。
四、向量的垂直概念两个向量a和b垂直的概念是指它们的方向互为正交。
具体来说,如果向量a与向量b的内积等于0,则表示它们垂直。
内积的定义为:a·b=x1*x2+y1*y2其中,x1和y1分别是向量a的x轴分量和y轴分量,x2和y2分别是向量b的x轴分量和y轴分量。
五、向量的垂直判断公式根据向量的垂直定义,可以推导出判断两个向量垂直的方法。
向量a 和向量b垂直的条件可以表示为:x1*x2+y1*y2=0这个条件说明,两个向量的内积为0时,它们是垂直的。
从几何上来看,这表示两个向量在坐标平面上的直角。
2020年人教版四年级数学上册《平行和垂直》试题(附答案)

新人教版四年级数学上册《平行和垂直》试题
1.填空题
(1)在()内不相交的两条直线叫做(),平行线间的距离处处()。
(2)长方形的长和宽互相()。
2.判断题
(1)不相交的两条直线叫做平行线。
()
(2)两条线段平行,它们一定相等。
()
(3)平行线之间的垂线只有一条。
()
(4)两条平行线之间的距离处处相等。
()
3.选择题
(1)有两条直线都和一条直线平行,这两条直线()。
①互相垂直②互相平行③相交
(2)过直线外的一点画已知直线的平行线,这样的平行线可以画()条。
①1条②2条③无数条
(3)在同一平面内不重合的两条直线()
①相交②平行③不相交就平行
4.画图题。
过点M画AB、AC的平行线。
参考答案
1.(1)同一平面,平行线,相等(2)垂直
2.(1)×(2)×(3)√(4)√
3.(1)②互相平行(2)①1条(3)③不相交就平行4.。
人教A版高中数学选修2-1课件:3-2立体几何中的向量方法 第4课时 空间向量的平行、垂直关系

探究 1:求平面的法向量 【例 1】
如图,已知四边形 ABCD 是直角梯形,∠ABC=90°,SA⊥平面 ABCD,SA=AB=BC=1,AD= ,试建立适当的坐标系,求: (1)平面 ABCD 与平面 SAB 的一个法向量; (2)平面 SCD 的一个法向量.
1 2
【方法指导】一般情况下,使用待定系数法求平面的法向量 的步骤:①设出平面的法向量为 n=(x,y,z);②找出(求出)平面内 的两个不共线的向量 a=(a1,b1,c1),b=(a2,b2,c2);③根据法向量的 定义建立关于 x,y,z 的方程组 一个解,即得法向量. n·a = 0, n·b = 0; ④解方程组,取其中的
【解析】不妨设正方体的边长为 a,建立空间直角坐标系 Dxyz(如图),则 E(a,2,0),F(2,a,0),G(a,0,2). 设平面 EFG 的法向量为 n=(x,y,z), GE=(0,2,-2),
a a FE=( ,- ,0), 2 2 1 1 a a a a a
n ⊥ GE,⇒ 1 1 n ⊥ FE n·FE = x- y = 0,
2
2
2
2
(法二)以CD,CB,CE为正交基底,建立空间直角坐标系,则 E(0,0,1),D( 2,0,0),B(0, 2,0),A( 2, 2,0),M( , ,1),DE= (- 2,0,1),BE=(0,- 2,1),AM=(- 2 ,- 2 ,1). 设平面 BDE 的法向量为 n=(a,b,c),∴n⊥DE,n⊥BE, n·DE = 0, - 2a + c = 0, ∴ ∴ n·BE = 0, - 2b + c = 0, 令 c=1,则 a= 2 ,b= 2 ,n=( 2 , 2 ,1),∴n·AM=0.
向量法证明平行与垂直-人教版高中数学

知识图谱-利用向量证明空间中的平行关系-利用向量证明空间中的垂直关系直线的方向向量与直线的向量方程利用向量方法证明线面平行关系利用向量方法证明线线与面面的平行关系利用向量方法证明线线垂直平面的法向量利用向量方法证明线面垂直利用向量方法证明面面垂直第02讲_向量法证明平行与垂直错题回顾利用向量证明空间中的平行关系知识精讲一.直线的方向向量与直线的向量方程1.点的位置向量在空间中,我们取一定点作为基点,那么空间中任意一点的位置就可以用向量来表示,我们把向量称为点的位置向量.2.直线的方向向量空间中任一直线的位置可以由上的一个定点以及一个定方向确定,如图,点是直线上的一点,向量表示直线的方向向量,则对于直线上任一点,有,这样点和向量,不仅可以确定直线的位置,还可具体表示出上的任意点;直线上的向量以及与共线的向量叫做的方向向量.3.直线的向量方程直线上任意一点,一定存在实数,使得①,①式可以看做直线的参数方程,直线的参数方程还可以作如下表示:对空间中任意一确定点,点在直线上的充要条件是存在唯一的实数满足等式②,如果在上取,则上式可以化为③;①②③都叫做空间直线的向量参数方程.二.平面的法向量1.平面法向量的定义已知平面,如果向量的基线与平面垂直,则向量叫作平面的法向量或者说向量与平面正交.2.平面法向量的性质(1)平面上的一个法向量垂直于平面共面的所有向量;(2)一个平面的法向量有无限多个,它们互相平行.三.用向量方法证明空间中的平行关系1.线线平行设直线的方向向量分别是,则要证明或与重合,只需要证明,即.2.线面平行(1)设直线的方向向量是,平面的法向量是,要证明,只需要证明;(2)根据线面平行的判定定理:如果直线(平面外)与平面内的一条直线平行,那么这条直线与这个平面平行;所以,要证明一条直线和一个平面平行,也可以在平面内找到一个向量与已知直线的方向向量是共线向量即可;(3)根据共面向量定理可知:如果一个向量和两个不共线的向量是共面向量,那么这个向量与这两个不共面向量确定的平面一定平行.已知两个不共线向量与平面共面,一条直线的一个方向向量为,则由共面向量定理,可得或在内存在两个实数,使.3.面面平行(1)若能求出平面的法向量,要证明,只需要证明即可.(2)由面面平行的判定定理:要证明面面平行,只要转化为相应的线面平行、线线平行即可,已知两个不共线的向量与平面共面,则由两平面平行的判定与性质,得.三点剖析一.方法点拨1.在平面内,直线的向量方程可类比点斜式方程,直线的方向向量、斜率都是刻画直线方向的量,只是从不同角度引入,它们有一定的关系:斜率为的直线,其方向向量为,反之,方向向量为的直线不一定存在斜率;在空间中,用方向向量刻画直线较为方便.2.空间中建系描述选取三条两两相交的直线的交点作为原点,以哪三条直线为轴,建立空间直角坐标系.例如:正方体中,建系的描述为:以点为坐标原点,分别以所在直线为轴,建立空间直角坐标系.3.用空间向量证明平行关系需要注意的问题(1)用空间向量的方法证明立体几何中的平行问题,主要运用了直线的方向向量和平面的法向量,同时也要借助空间中已有的一些关于平行的定理.(2)用向量方法证明平行问题的步骤①建立空间图形与空间向量的关系,用空间向量表示问题中涉及的点、直线、平面;②通过向量运算研究平行问题;③根据运算结果解释相关问题.4.平面法向量的求法(1)建立适当的坐标系;(2)设出平面法向量为;(3)找出(求出)平面内的两个共线的向量的坐标;(4)根据法向量的定义建立关于的方程组;(5)解方程组,取其中的一个解,即得法向量,由于一个平面的法向量有无数个,故可在代入方程组的解中取一个最简单的作为平面的法向量.有时候,题目中的线面垂直条件比较明显,可以将垂线的方向向量作为平面的法向量来解决问题.题模精讲题模一直线的方向向量与直线的向量方程例1.1、已知向量=(2,4,5),=(3,x,y)分别是直线l1、l2的方向向量,若l1∥l2,则()A、x=6,y=15B、x=3,y=C、x=3,y=15D、x=6,y=例1.2、从点沿向量的方向取线段长,则B点的坐标为( )A、B、C、D、题模二平面的法向量例2.1、在空间直角坐标系内,设平面经过点,平面的法向量为,为平面内任意一点,求满足的关系式.例2.2、(1)设平面的法向量为,平面的法向量为,若,则__________;则__________.(2)若的方向向量为,平面的法向量为,若,则__________;若,则__________.题模三利用向量方法证明线面平行关系例3.1、已知正方形和正方形相交于分别在上,且,求证平面.例3.2、在正方体中,的中点,求证:.题模四利用向量方法证明线线与面面的平行关系例4.1、在正方体中,分别是的中点.证明:.例4.2、如右图所示,在平行六面体中,分别是的中点.求证:平面∥平面..随堂练习随练1.1、已知,,则直线的模为的方向向量是________________.随练1.2、已知点若点为直线上任意一点,则直线的向量参数方程为______________,当时,点的坐标为______________.随练1.3、已知,且均与平面平行,直线的方向向量,则()随练1.4、若两个不同平面的法向量分别为,则( )A、B、C、相交但不垂直D、以上均不正确随练1.5、已知平面经过三点,试求平面的一个法向量.随练1.6、在正方体中,分别是的中点,求证:.随练1.7、已知正方体的棱长为2,分别是的中点,求证:(1);(2).利用向量证明空间中的垂直关系知识精讲一.直线方向向量与平面法向量在确定直线、平面位置关系中的应用设空间两条直线的方向向量分别是,两个平面的法向量分别是,则有下表与与与二.用向量方法证明空间中的垂直关系1.线线垂直设直线的方向向量分别是,则要证明,只需要证明,即.2.线面垂直(1)设直线的方向向量是,平面的法向量是,要证明,只需要证明.(2)根据线面垂直的判定定理,转化为直线与平面内的两条相交直线垂直.3.面面垂直(1)根据面面垂直的判定定理转化为证相应的线面垂直,线线垂直;(2)证明两个平面的法向量互相垂直.一、方法点拨1.平面法向量可以不唯一,只要是垂直于平面的直线,其方向向量都可以当作法向量进行运算.2.平面中的平行、垂直关系的向量论证,注意复习线面、面面平行与垂直的判定定理,将这种位置关系的判断转化为向量间的代数运算,体现了向量的工具性功能.题模精讲题模一利用向量方法证明线线垂直例1.1、设的方向向量,的方向向量,若,则( )A、1B、2C、D、3例1.2、在正三棱柱中,.求证:.题模二利用向量方法证明线面垂直若直线的方向向量为,平面的法向量为,则( )A、B、C、D、斜交例2.2、在正方体中,分别是棱的中点,试在棱上找一点,使得.题模三利用向量方法证明面面垂直例3.1、若两个不同平面的法向量分别为,则( )A、B、C、相交但不垂直D、以上均不正确例3.2、在长方体中,,分别是棱的中点.(1)求证:平面;(2)求证:平面平面.随堂练习随练2.1、如图所示,已知空间四边形的各边和对角线的长都等于,点分别是的中点.求证:随练2.2、如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.(1)证明PA∥平面EDB;(2)证明PB⊥平面EFD;(3)求二面角C-PB-D的大小.随练2.3、在正棱锥中,三条侧棱两两互相垂直,的重心,分别为上的点,且(1)求证:平面;(2)求证:的公垂线段.自我总结课后作业作业1、已知,把按向量平移后所得的向量是( )A、B、C、D、作业2、正四面体的高的中点为,则平面的一个法向量可以是________,平面的一个法向量可以是________.作业3、若直线是两条异面直线,它们的方向向量分别是,则直线的公垂线(与两异面直线垂直相交的直线)的一个方向向量是________.作业4、是正四棱柱,侧棱长为3,底面边长为2,E是棱BC的中点,求证:.作业5、如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点,(1)求证:AC⊥BC1;(2)求证:AC1∥平面CDB1;(3)求二面角C1-AB-C的余弦值.作业6、已知空间三点A(0,2,3),B(-2,1,6),C(1,-1,5)求:(1)求以向量,为一组邻边的平行四边形的面积S;(2)若向量分别与向量,垂直,且||=,求向量的坐标.作业7、如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,作EF⊥PB交PB于点F.(1)证明:PA∥平面EDB;(2)证明:PB⊥平面EFD.作业8、在直三棱柱中,底面是以为直角的等腰直角三角形,,的中点,在线段,使?若存在,求出;若不存在,请说明理由.作业9、如图,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BA D=∠FAB=90°,BC AD,BE AF,G,H分别为FA,FD的中点(Ⅰ)证明:四边形BCHG是平行四边形;(Ⅱ)C,D,F,E四点是否共面?为什么?(Ⅲ)设AB=BE,证明:平面ADE⊥平面CDE.。
人教版高考数学(理)全国通用版:第八章立体几何与空间向量证明平行与垂直
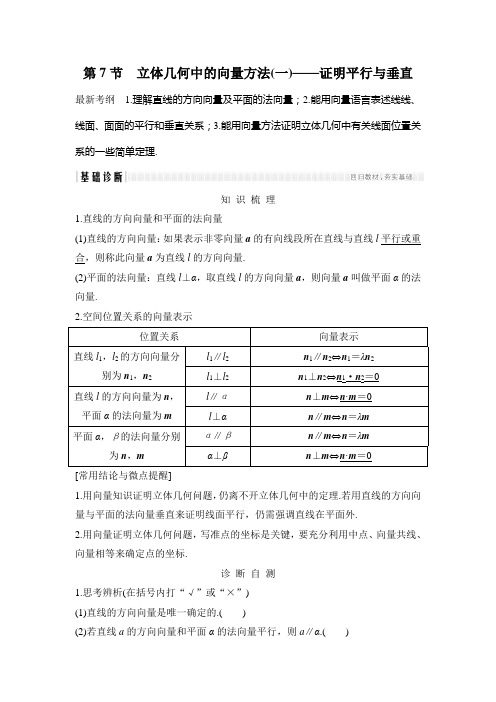
第7节 立体几何中的向量方法(一)——证明平行与垂直最新考纲 1.理解直线的方向向量及平面的法向量;2.能用向量语言表述线线、线面、面面的平行和垂直关系;3.能用向量方法证明立体几何中有关线面位置关系的一些简单定理.知 识 梳 理1.直线的方向向量和平面的法向量(1)直线的方向向量:如果表示非零向量a 的有向线段所在直线与直线l 平行或重合,则称此向量a 为直线l 的方向向量.(2)平面的法向量:直线l ⊥α,取直线l 的方向向量a ,则向量a 叫做平面α的法向量.2.空间位置关系的向量表示[常用结论与微点提醒]1.用向量知识证明立体几何问题,仍离不开立体几何中的定理.若用直线的方向向量与平面的法向量垂直来证明线面平行,仍需强调直线在平面外.2.用向量证明立体几何问题,写准点的坐标是关键,要充分利用中点、向量共线、向量相等来确定点的坐标.诊 断 自 测1.思考辨析(在括号内打“√”或“×”) (1)直线的方向向量是唯一确定的.( )(2)若直线a 的方向向量和平面α的法向量平行,则a ∥α.( )(3)若两平面的法向量平行,则两平面平行.( )(4)若直线a 的方向向量与平面α的法向量垂直,则a ∥α.( ) 解析 (1)直线的方向向量不是唯一的,有无数多个; (2)a ⊥α;(3)两平面平行或重合;(4)a ∥α或a ⊂α. 答案 (1)× (2)× (3)× (4)×2.(选修2-1P104练习2改编)已知平面α,β的法向量分别为n 1=(2,3,5),n 2=(-3,1,-4),则( ) A.α∥βB.α⊥βC.α,β相交但不垂直D.以上均不对解析 ∵n 1≠λn 2,且n 1·n 2=2×(-3)+3×1+5×(-4)=-23≠0,∴α,β相交但不垂直. 答案 C3.若直线l 的方向向量为a =(1,0,2),平面α的法向量为n =(-2,0,-4),则( ) A.l ∥α B.l ⊥α C.l ⊂αD.l 与α斜交解析 ∵a =(1,0,2),n =(-2,0,-4), ∴n =-2a ,即a ∥n .∴l ⊥α. 答案 B4.已知A (1,0,0),B (0,1,0),C (0,0,1),则下列向量是平面ABC 法向量的是( )A.(-1,1,1)B.(1,-1,1)C.⎝ ⎛⎭⎪⎫-33,-33,-33D.⎝ ⎛⎭⎪⎫33,33,-33解析 设n =(x ,y ,z )为平面ABC 的法向量, 则⎩⎨⎧n ·AB →=0,n ·AC →=0,化简得⎩⎪⎨⎪⎧-x +y =0,-x +z =0,∴x =y =z .答案 C5.如图所示,在正方体ABCD -A 1B 1C 1D 1中,O 是底面正方形ABCD 的中心,M 是D 1D 的中点,N 是A 1B 1的中点,则直线ON ,AM 的位置关系是________.解析 以A 为原点,分别以AB →,AD →,AA 1→所在直线为x ,y ,z轴,建立空间直角坐标系(图略),设正方体的棱长为1,则A (0,0,0),M ⎝ ⎛⎭⎪⎫0,1,12,O ⎝ ⎛⎭⎪⎫12,12,0,N ⎝ ⎛⎭⎪⎫12,0,1.AM →·ON →=⎝ ⎛⎭⎪⎫0,1,12·⎝ ⎛⎭⎪⎫0,-12,1=0,∴ON 与AM 垂直. 答案 垂直考点一 利用空间向量证明平行问题【例1】 (一题多解)如图,在四面体ABCD 中,AD ⊥平面BCD ,BC ⊥CD ,AD =2,BD =22,M 是AD 的中点,P 是BM 的中点,点Q 在线段AC 上,且AQ =3QC . 证明:PQ ∥平面BCD .证明 法一 如图,取BD 的中点O ,以O 为原点,OD ,OP 所在射线分别为y ,z 轴的正半轴,建立空间直角坐标系O -xyz .由题意知,A (0,2,2),B (0,-2,0),D (0,2,0). 设点C 的坐标为(x 0,y 0,0). 因为AQ→=3QC →, 所以Q ⎝ ⎛⎭⎪⎫34x 0,24+34y 0,12.因为M 为AD 的中点,故M (0,2,1). 又P 为BM 的中点,故P ⎝ ⎛⎭⎪⎫0,0,12,所以PQ→=⎝ ⎛⎭⎪⎫34x 0,24+34y 0,0.又平面BCD 的一个法向量为a =(0,0,1),故PQ →·a =0. 又PQ ⊄平面BCD , 所以PQ ∥平面BCD .法二 在线段CD 上取点F ,使得DF =3FC ,连接OF ,同法一建立空间直角坐标系,写出点A ,B ,C 的坐标,设点C 坐标为(x 0,y 0,0). ∵CF→=14CD →,设点F 坐标为(x ,y ,0),则 (x -x 0,y -y 0,0)=14(-x 0,2-y 0,0), ∴⎩⎪⎨⎪⎧x =34x 0,y =24+34y 0,∴OF→=⎝ ⎛⎭⎪⎫34x 0,24+34y 0,0 又由法一知PQ→=⎝ ⎛⎭⎪⎫34x 0,24+34y 0,0, ∴OF→=PQ →,∴PQ ∥OF .又PQ ⊄平面BCD ,OF ⊂平面BCD , ∴PQ ∥平面BCD .规律方法 1.恰当建立坐标系,准确表示各点与相关向量的坐标,是运用向量法证明平行和垂直的关键.2.证明直线与平面平行,只须证明直线的方向向量与平面的法向量的数量积为零,或证直线的方向向量与平面内的不共线的两个向量共面,或证直线的方向向量与平面内某直线的方向向量平行,然后说明直线在平面外即可.这样就把几何的证明问题转化为向量运算.【训练1】 已知正方体ABCD -A1B 1C 1D 1的棱长为1,E ,F ,G 分别为AB ,AD ,AA 1的中点,求证:平面EFG ∥平面B 1CD 1. 证明 建立如图所示的空间直角坐标系D -xyz ,则A (1,0,0),B (1,1,0),C (0,1,0),D (0,0,0),A 1(1,0,1),B 1(1,1,1),D 1(0,0,1).得E ⎝ ⎛⎭⎪⎫1,12,0,F ⎝ ⎛⎭⎪⎫12,0,0,G ⎝ ⎛⎭⎪⎫1,0,12,EF →=⎝ ⎛⎭⎪⎫-12,-12,0,EG →=⎝ ⎛⎭⎪⎫0,-12,12. 设n 1=(x 1,y 1,z 1)为平面EFG 的法向量,n 2=(x 2,y 2,z 2)为平面B 1CD 1的一个法向量.则⎩⎪⎨⎪⎧n 1·EF →=0,n 1·EG →=0,即⎩⎪⎨⎪⎧-12x 1-12y 1=0,-12y 1+12z 1=0.令x 1=1,可得y 1=-1,z 1=-1, 同理可得x 2=1,y 2=-1,z 2=-1. 则n 1=(1,-1,-1),n 2=(1,-1,-1). 由n 1=n 2,得平面EFG ∥平面B 1CD 1. 考点二 利用空间向量证明垂直问题【例2】 如图所示,已知四棱锥P -ABCD 的底面是直角梯形,∠ABC =∠BCD =90°,AB =BC =PB =PC =2CD ,侧面PBC ⊥底面ABCD .证明: (1)P A ⊥BD ;(2)平面P AD ⊥平面P AB .证明 (1)取BC 的中点O ,连接PO ,∵平面PBC ⊥底面ABCD ,BC 为交线,PO ⊂平面PBC ,△PBC 为等边三角形,即PO ⊥BC , ∴PO ⊥底面ABCD .以BC 的中点O 为坐标原点,以BC 所在直线为x 轴,过点O 与AB 平行的直线为y 轴,OP 所在直线为z 轴,建立空间直角坐标系,如图所示.不妨设CD =1,则AB =BC =2,PO = 3.∴A (1,-2,0),B (1,0,0),D (-1,-1,0),P (0,0,3).∴BD →=(-2,-1,0),P A →=(1,-2,-3). ∵BD →·P A →=(-2)×1+(-1)×(-2)+0×(-3)=0, ∴P A →⊥BD →, ∴P A ⊥BD .(2)取P A 的中点M ,连接DM ,则M ⎝ ⎛⎭⎪⎫12,-1,32.∵DM →=⎝ ⎛⎭⎪⎫32,0,32,PB →=(1,0,-3),∴DM →·PB →=32×1+0×0+32×(-3)=0, ∴DM→⊥PB →,即DM ⊥PB . ∵DM →·P A →=32×1+0×(-2)+32×(-3)=0, ∴DM →⊥P A →,即DM ⊥P A .又∵P A ∩PB =P ,P A ,PB ⊂平面P AB , ∴DM ⊥平面P AB . ∵DM ⊂平面P AD , ∴平面P AD ⊥平面P AB .规律方法 1.利用已知的线面垂直关系构建空间直角坐标系,准确写出相关点的坐标,从而将几何证明转化为向量运算.其中灵活建系是解题的关键. 2.用向量证明垂直的方法(1)线线垂直:证明两直线所在的方向向量互相垂直,即证它们的数量积为零. (2)线面垂直:证明直线的方向向量与平面的法向量共线,或将线面垂直的判定定理用向量表示.(3)面面垂直:证明两个平面的法向量垂直,或将面面垂直的判定定理用向量表示.【训练2】 如图,四棱柱ABCD -A 1B 1C 1D 1的底面ABCD 是正方形,O 为底面中心,A 1O ⊥平面ABCD ,AB =AA 1= 2.证明:A 1C ⊥平面BB 1D 1D .证明 由题设易知OA ,OB ,OA 1两两垂直,以O 为原点建立如图所示的空间直角坐标系.因为AB =AA 1=2,所以OA =OB =OA 1=1,所以A (1,0,0),B (0,1,0), C (-1,0,0),D (0,-1,0),A 1(0,0,1). 由A 1B 1→=AB →,易得B 1(-1,1,1).因为A 1C →=(-1,0,-1),BD →=(0,-2,0),BB 1→=(-1,0,1), 所以A 1C →·BD →=0,A 1C →·BB 1→=0, 所以A 1C ⊥BD ,A 1C ⊥BB 1.又BD ∩BB 1=B ,BD ,BB 1⊂平面BB 1D 1D , 所以A 1C ⊥平面BB 1D 1D .考点三 用空间向量解决探索性问题(多维探究) 命题角度1 与平行有关的探索性问题【例3-1】 (2016·北京卷改编)如图,在四棱锥P -ABCD 中,平面P AD ⊥平面ABCD ,P A ⊥PD ,P A =PD ,AB ⊥AD ,AB =1,AD =2,AC =CD = 5.(1)求证:PD ⊥平面P AB ;(2)在棱P A 上是否存在点M ,使得BM ∥平面PCD ?若存在,求AMAP 的值;若不存在,说明理由.(1)证明 因为平面P AD ⊥平面ABCD ,AB ⊥AD , 所以AB ⊥平面P AD ,所以AB ⊥PD .又因为P A ⊥PD 且AB ∩P A =A ,P A ,AB ⊂平面P AB ,所以PD ⊥平面P AB . (2)解 取AD 的中点O ,连接PO ,CO . 因为P A =PD ,所以PO ⊥AD .又因为PO ⊂平面P AD ,平面P AD ⊥平面ABCD , 所以PO ⊥平面ABCD .因为CO ⊂平面ABCD ,所以PO ⊥CO . 因为AC =CD ,所以CO ⊥AD .如图,建立空间直角坐标系O -xyz .由题意得,A (0,1,0),B (1,1,0),C (2,0,0), D (0,-1,0),P (0,0,1).设M 是棱P A 上一点,则存在λ∈[0,1],使得AM →=λAP →.因此M (0,1-λ,λ),BM→=(-1,-λ,λ).因为BM ⊄平面PCD ,所以BM ∥平面PCD , 当且仅当BM→·n =0,即(-1,-λ,λ)·(1,-2,2)=0,解得λ=14. 所以在棱P A 上存在点M ,使得BM ∥平面PCD , 此时AM AP =14.命题角度2 与垂直有关的探索性问题【例3-2】 如图,正方形ADEF 所在平面和等腰梯形ABCD 所在的平面互相垂直,已知BC =4,AB =AD =2. (1)求证:AC ⊥BF ;(2)在线段BE 上是否存在一点P ,使得平面P AC ⊥平面BCEF ?若存在,求出BP PE 的值;若不存在,请说明理由.(1)证明 ∵平面ADEF ⊥平面ABCD ,平面ADEF ∩平面ABCD =AD ,AF ⊥AD ,AF ⊂平面ADEF , ∴AF ⊥平面ABCD .又AC ⊂平面ABCD ,∴AF ⊥AC .过A 作AH ⊥BC 于H ,则BH =1,AH =3,CH =3, ∴AC =23,∴AB 2+AC 2=BC 2,∴AC ⊥AB , ∵AB ∩AF =A ,AB ,AF ⊂平面F AB , ∴AC ⊥平面F AB ,∵BF ⊂平面F AB ,∴AC ⊥BF .(2)解 存在.由(1)知,AF ,AB ,AC 两两垂直,以A 为坐标原点,AB→,AC →,AF →的方向分别为x 轴,y 轴,z 轴正方向,建立如图所示的空间直角坐标系A -xyz ,则A (0,0,0),B (2,0,0),C (0,23,0),E (-1,3,2).假设在线段BE 上存在一点P 满足题意,则易知点P 不与点B ,E 重合, 设BP →=λPE →,则λ>0,P ⎝ ⎛⎭⎪⎫2-λ1+λ,3λ1+λ,2λ1+λ. 设平面P AC 的法向量为m =(x ,y ,z ).由AP →=⎝ ⎛⎭⎪⎫2-λ1+λ,3λ1+λ,2λ1+λ,AC →=(0,23,0), 得⎩⎨⎧m ·AP →=2-λ1+λx +3λ1+λy +2λ1+λz =0,m ·AC →=23y =0,即⎩⎪⎨⎪⎧y =0,z =λ-22λx ,令x =1,则z =λ-22λ, 所以m =⎝⎛⎭⎪⎫1,0,λ-22λ为平面P AC 的一个法向量.同理,可求得n =⎝ ⎛⎭⎪⎫1,33,1为平面BCEF 的一个法向量.当m ·n =0,即λ=23时,平面P AC ⊥平面BCEF ,故存在满足题意的点P ,此时BP PE =23.规律方法 解决立体几何中探索性问题的基本方法(1)通常假设题中的数学对象存在(或结论成立),然后在这个前提下进行逻辑推理. (2)探索性问题的关键是设点:①空间中的点可设为(x ,y ,z );②坐标平面内的点其中一个坐标为0,如xOy 面上的点为(x ,y ,0);③坐标轴上的点两个坐标为0,如z 轴上的点为(0,0,z );④直线(线段)AB 上的点P ,可设为AP →=λAB →,表示出点P 的坐标,或直接利用向量运算.提醒 解这类问题时要利用好向量垂直和平行的坐标表示.【训练3】 如图,在三棱柱ABC -A 1B 1C 1中,AA 1C 1C 是边长为4的正方形.平面ABC ⊥平面AA 1C 1C ,AB =3,BC =5. (1)求证:AA 1⊥平面ABC ;(2)证明:在线段BC 1上存在点D ,使得AD ⊥A 1B ,并求BDBC 1的值.证明 (1)因为AA 1C 1C 为正方形,所以AA 1⊥AC .因为平面ABC ⊥平面AA 1C 1C ,AA 1⊂平面AA 1C 1C ,且AA 1垂直于这两个平面的交线AC ,所以AA 1⊥平面ABC .(2)由(1)知AA 1⊥AB ,AA 1⊥AC .由题知AB =3,BC =5,AC =4,所以AB ⊥AC . 如图,以A 为原点建立空间直角坐标系A -xyz .则B (0,3,0),A 1(0,0,4),B 1(0,3,4),C 1(4,0,4). 设D (x ,y ,z )是直线BC 1上的一点,且BD →=λBC →1,所以(x ,y -3,z )=λ(4,-3,4), 解得x =4λ,y =3-3λ,z =4λ, 所以AD→=(4λ,3-3λ,4λ). 由AD →·A 1B →=0,A 1B →=(0,3,-4), 则9-25λ=0,解得λ=925.因为925∈[0,1],所以在线段BC 1上存在点D ,使得AD ⊥A 1B ,此时,BD BC 1=λ=925.基础巩固题组 (建议用时:40分钟)一、选择题1.平面α的法向量为(1,2,-2),平面β的法向量为(-2,-4,k ),若α∥β,则k 等于( ) A.2B.-4C.4D.-2解析 ∵α∥β,∴两平面的法向量平行, ∴-21=-42=k -2,∴k =4.答案 C2.若AB →=λCD →+μCE →,则直线AB 与平面CDE 的位置关系是( ) A.相交 B.平行C.在平面内D.平行或在平面内解析 ∵AB→=λCD →+μCE →,∴AB →,CD →,CE →共面.则AB 与平面CDE 的位置关系是平行或在平面内.答案 D3.已知平面α内有一点M (1,-1,2),平面α的一个法向量为n =(6,-3,6),则下列点P 中,在平面α内的是( ) A.P (2,3,3)B.P (-2,0,1)C.P (-4,4,0)D.P (3,-3,4)解析 逐一验证法,对于选项A ,MP →=(1,4,1),∴MP→·n =6-12+6=0,∴MP →⊥n , ∴点P 在平面α内,同理可验证其他三个点不在平面α内. 答案 A4.(2018·郑州月考)如图,F 是正方体ABCD -A 1B 1C 1D 1的棱CD 的中点.E 是BB 1上一点,若D 1F ⊥DE ,则有( ) A.B 1E =EB B.B 1E =2EB C.B 1E =12EB D.E 与B 重合解析 分别以DA ,DC ,DD 1为x ,y ,z 轴建立空间直角坐标系,设正方形的边长为2,则D (0,0,0),F (0,1,0),D 1(0,0,2),设E (2,2,z ),D 1F →=(0,1,-2),DE →=(2,2,z ),∵D 1F →·DE →=0×2+1×2-2z =0,∴z =1,∴B 1E =EB . 答案 A5.如图所示,在正方体ABCD -A1B 1C 1D 1中,棱长为a ,M ,N 分别为A 1B 和AC 上的点,A 1M =AN =2a 3,则MN 与平面BB 1C 1C 的位置关系是( ) A.斜交B.平行C.垂直D.MN 在平面BB 1C 1C 内解析 建立如图所示的空间直角坐标系, 由于A 1M =AN =2a3,则M ⎝ ⎛⎭⎪⎫a ,2a 3,a 3,N ⎝ ⎛⎭⎪⎫2a 3,2a 3,a , MN →=⎝ ⎛⎭⎪⎫-a 3,0,2a 3. 又C 1D 1⊥平面BB 1C 1C ,所以C 1D 1→=(0,a ,0)为平面BB 1C 1C 的一个法向量. 因为MN →·C 1D 1→=0,所以MN →⊥C 1D 1→,又MN ⊄平面BB 1C 1C , 所以MN ∥平面BB 1C 1C . 答案 B二、填空题6.(2018·武汉调研)已知平面α内的三点A (0,0,1),B (0,1,0),C (1,0,0),平面β的一个法向量n =(-1,-1,-1),则不重合的两个平面α与β的位置关系是________.解析 设平面α的法向量为m =(x ,y ,z ), 由m ·AB →=0,得x ·0+y -z =0⇒y =z , 由m ·AC →=0,得x -z =0⇒x =z ,取x =1, ∴m =(1,1,1),m =-n ,∴m ∥n ,∴α∥β. 答案 α∥β7.(2018·西安调研)已知AB →=(1,5,-2),BC →=(3,1,z ),若AB →⊥BC →,BP →=(x -1,y ,-3),且BP ⊥平面ABC ,则实数x +y =________.解析由条件得⎩⎪⎨⎪⎧3+5-2z =0,x -1+5y +6=0,3(x -1)+y -3z =0,解得x =407,y =-157,z =4, ∴x +y =407-157=257. 答案 2578.已知点P 是平行四边形ABCD 所在的平面外一点,如果AB →=(2,-1,-4),AD →=(4,2,0),AP→=(-1,2,-1).对于结论:①AP ⊥AB ;②AP ⊥AD ;③AP →是平面ABCD 的法向量;④AP →∥BD →.其中正确的序号是________.解析 ∵AB→·AP →=0,AD →·AP →=0,∴AB ⊥AP ,AD ⊥AP ,则①②正确.又AB →与AD →不平行,∴AP→是平面ABCD 的法向量,则③正确. 由于BD→=AD →-AB →=(2,3,4),AP →=(-1,2,-1), ∴BD→与AP →不平行,故④错误. 答案 ①②③ 三、解答题9.(一题多解)如图所示,平面P AD ⊥平面ABCD ,ABCD 为正方形,△P AD 是直角三角形,且P A =AD =2,E ,F ,G 分别是线段P A ,PD ,CD 的中点.求证:PB ∥平面EFG . 证明 ∵平面P AD ⊥平面ABCD ,且ABCD 为正方形, ∴AB ,AP ,AD 两两垂直.以A 为坐标原点,建立如右图所示的空间直角坐标系A -xyz ,则A (0,0,0),B (2,0,0),C (2,2,0),D (0,2,0),P (0,0,2),E (0,0,1),F (0,1,1),G (1,2,0). 法一 ∴EF→=(0,1,0),EG →=(1,2,-1),设平面EFG 的法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧n ·EF →=0,n ·EG →=0,即⎩⎨⎧y =0,x +2y -z =0,令z =1,则n =(1,0,1)为平面EFG 的一个法向量, ∵PB→=(2,0,-2),∴PB →·n =0,∴n ⊥PB →, ∵PB ⊄平面EFG ,∴PB ∥平面EFG .法二 PB→=(2,0,-2),FE →=(0,-1,0),FG→=(1,1,-1).设PB →=sFE →+tFG →, 即(2,0,-2)=s (0,-1,0)+t (1,1,-1),∴⎩⎨⎧t =2,t -s =0,-t =-2,解得s =t =2.∴PB →=2FE →+2FG →,又∵FE→与FG →不共线,∴PB →,FE →与FG →共面. ∵PB ⊄平面EFG , ∴PB ∥平面EFG .10.如图正方形ABCD 的边长为22,四边形BDEF 是平行四边形,BD 与AC 交于点G ,O 为GC 的中点,FO =3,且FO ⊥平面ABCD .(1)求证:AE ∥平面BCF ; (2)求证:CF ⊥平面AEF .证明 取BC 中点H ,连接OH ,则OH ∥BD , 又四边形ABCD 为正方形,∴AC ⊥BD ,∴OH ⊥AC ,故以O 为原点,建立如图所示的直角坐标系,则A (3,0,0),C (-1,0,0),D (1,-2,0),F (0,0,3),B (1,2,0).BC→=(-2,-2,0),CF →=(1,0,3),BF →=(-1,-2,3).(1)设平面BCF 的法向量为n =(x ,y ,z ), 则⎩⎨⎧-2x -2y =0,x +3z =0,取z =1,得n =(-3,3,1). 又四边形BDEF 为平行四边形, ∴DE→=BF →=(-1,-2,3), ∴AE→=AD →+DE →=BC →+BF → =(-2,-2,0)+(-1,-2,3)=(-3,-4,3), ∴AE→·n =33-43+3=0,∴AE →⊥n , 又AE ⊄平面BCF ,∴AE ∥平面BCF .(2)AF →=(-3,0,3),∴CF →·AF →=-3+3=0,CF →·AE →=-3+3=0,∴CF →⊥AF →,CF →⊥AE →, 又AE ∩AF =A , AE ,AF ⊂平面AEF , ∴CF ⊥平面AEF .能力提升题组 (建议用时:20分钟)11.如图,正方形ABCD 与矩形ACEF 所在平面互相垂直,AB =2,AF =1,M 在EF 上,且AM ∥平面BDE .则M 点的坐标为( )A.(1,1,1)B.⎝ ⎛⎭⎪⎫23,23,1 C.⎝ ⎛⎭⎪⎫22,22,1D.⎝⎛⎭⎪⎫24,24,1解析 设AC 与BD 相交于O 点,连接OE ,由AM ∥平面BDE ,且AM ⊂平面ACEF ,平面ACEF ∩平面BDE =OE ,∴AM ∥EO , 又O 是正方形ABCD 对角线交点, ∴M 为线段EF 的中点.在空间坐标系中,E (0,0,1),F (2,2,1). 由中点坐标公式,知点M 的坐标⎝ ⎛⎭⎪⎫22,22,1.答案 C12.如图,正方体ABCD -A1B 1C 1D 1的棱长为1,E ,F 分别是棱BC ,DD 1上的点,如果B 1E ⊥平面ABF ,则CE 与DF 的和的值为________.解析 以D 1A 1,D 1C 1,D 1D 分别为x ,y ,z 轴建立空间直角坐标系,设CE =x ,DF =y ,则易知E (x ,1,1),B 1(1,1,0),F (0,0,1-y ),B (1,1,1), ∴B 1E →=(x -1,0,1),∴FB →=(1,1,y ), 由于B 1E ⊥平面ABF ,所以FB →·B 1E →=(1,1,y )·(x -1,0,1)=0⇒x +y =1. 答案 113.如图,正△ABC 的边长为4,CD 为AB 边上的高,E ,F 分别是AC 和BC 边的中点,现将△ABC 沿CD 翻折成直二面角A -DC -B .(1)试判断直线AB 与平面DEF 的位置关系,并说明理由;(2)在线段BC 上是否存在一点P ,使AP ⊥DE ?如果存在,求出BPBC 的值;如果不存在,请说明理由.解 (1)AB ∥平面DEF ,理由如下:在△ABC 中,由E ,F 分别是AC ,BC 的中点,得EF ∥AB . 又因为AB ⊄平面DEF ,EF ⊂平面DEF , 所以AB ∥平面DEF .(2)以点D 为坐标原点,直线DB ,DC ,DA 分别为x 轴,y 轴,z 轴,建立空间直角坐标系(如图所示),则A (0,0,2),B (2,0,0),C (0,23,0),E (0,3,1),故DE→=(0,3,1).假设存在点P (x ,y ,0)满足条件,则AP →=(x ,y ,-2),AP →·DE →=3y -2=0, 所以y =233.又BP→=(x -2,y ,0),PC →=(-x ,23-y ,0),BP →∥PC →, 所以(x -2)(23-y )=-xy ,所以3x +y =2 3. 把y =233代入上式得x =43,所以BP→=13BC →, 所以在线段BC 上存在点P 使AP ⊥DE ,此时BP BC =13.。
最新-2018高中数学 第3章321用向量方法解决平行与垂直问题课件 新人教A版选修2-1 精品

∵D1M⊥平面 EFB1,∴D1M⊥EF,D1M⊥B1E, ∴D→1M·E→F=0 且D→1M·B→1E=0,
于是-2+2=0, -2-2m-2=0,
∴m=1,
故取 B1B 的中点为 M 就能满足 D1M⊥平面 EFB1.
方法感悟 1.直线的方向向量和平面的法向量是用空间向量 解决立体几何问题的两个重要工具,是实现空间问 题的向量解法的媒介. 2.用空间向量方法证明立体几何中的平行与垂直 问题,主要运用了直线的方向向量和平面的法向量, 同时也要借助空间中已有的一些关于平行、垂直的 定理.
知新益能
1.平面的法向量 直线l⊥平面α,取直线l的_方__向__向__量___a,则a叫做 平面α的法向量. 2.空间中平行关系的向量表示
设直线l,m的方向向量分别为a=(a1, 线线平行 bl∥1,mc⇔1),_a_b∥_=_b_(_a.2,b2,c2),则
设直线l的方向向量为a=(a1,b1,c1), 线面平行 平面α的法向量为u=(a2,b2,c2),则
3.用向量方法证明平行、垂直问题的步骤: (1)建立空间图形与空间向量的关系(可以建立空 间直角坐标系,也可以不建系),用空间向量表 示问题中涉及的点、直线、平面; (2)通过向量运算研究平行、垂直问题; (3)根据运算结果解释相关问题.
问题探究 一个平面的法向量惟一吗? 提示:不惟一.
课堂互动讲练
考点突破
平面的法向量的求解与判定
若要求出一个平面的法向量,一般要建立空间直角 坐标系,然后用待定系数法求解,一般步骤为: (1)设出平面法向量n=(x,y,z); (2)找出(求出)平面内的两个不共线向量a=(a1,b1, c1),b=(a2,b2,c2);
【思路点拨】
【解】 设平面 ABC 的法向量为 n=(x,y,z), ∵A(1,2,3),B(2,0,-1),C(3,-2,0), ∴A→B=(1,-2,-4),A→C=(2,-4,-3), 由题设得:
2023年人教版高考数学总复习第一部分考点指导第八章立体几何第五节空间向量的运算及其坐标表示

3.空间向量有关运算
(1)坐标运算:设a=x1,y1,z1 ,b=x2,y2,z2 , 则a+b= (x1 x2,y1 y2,z1 z2 ) ; a-b= (x1 x2,y1 y2,z1 z2 ) ; λa= (x1, y1,z1) .
(2)数量积运算:a·b= x1x2+y1y2+z1z2 = |a||b|cos〈a,b〉.
B.共面 C.共线 D.不共线
②对空间中四点 A,B,C,P,若A→P =81 A→B +18 A→C ,则 P,A,B,C 四点( )
A.不共面
B.共面 C.共线 D.不共线
பைடு நூலகம்
③对空间中四点 A,B,C,P,若空间任意一点 O 都有O→P =43 O→A +81 O→B +
1 8
O→ C
,则 P,A,B,C 四点(
(2)已知a=(2,-1,3),b=(-1,4,-2),c=(7,5,λ),若a,b,c三向量共
面,则实数λ等于(
A.672
B.673
) C.674
D.675
【解析】选D.由a,b,c三向量共面,设a=mb+nc,
则(2,-1,3)=m(-1,4,-2)+n(7,5,λ),
2=-m+7n
即 -1=4m+5n ,解得λ=675 . 3=-2m+nλ
=12
O→ A
+23
1 (2
O→ B
+12
O→ C
-21
O→ A
)=61
O→ A
+13
O→ B
+13
O→ C
,
所以x=16 ,y=13 ,z=13 .
答案:16 ,31 ,13
2.如图,在长方体ABCD-A1B1C1D1中,O为AC的中点. ①化简 A1O -12 A→B -21 A→D =________. ②用A→B ,A→D , AA1 表示 OC1 ,则 OC1 =________.
人教版高二数学立体几何中的平行与垂直

人教版高二数学立体几何中的平行与垂直立体几何是高中数学中的一个重要分支,它研究的是空间中的点、线和面的相互关系。
在立体几何中,平行和垂直是两个基本的概念。
了解和掌握平行和垂直的性质对于解决立体几何问题非常重要。
本文将重点讨论人教版高二数学教材中关于平行和垂直的内容和例题。
1. 平行线的判定及性质在立体几何中,两条直线平行的判定方法有很多种,例如:同位角相等、内错角相等、同旁内错角互补等。
我们以同位角相等为例进行讨论。
同位角相等是判断平行线的常用方法之一。
如果两条直线被一组平行线截断,那么同位角相等。
这一性质可以通过以下定理加以证明:定理1:如果两条直线被一组平行线截断,那么同位角相等。
根据这一定理,我们可以判定两条直线是否平行,进而解决立体几何中的相关问题。
2. 平行线之间的性质在立体几何中,平行线之间也有一些重要的性质。
下面我们来介绍其中的几个。
性质1:平行线与平行线之间的交线,叫做该平行线的截线。
如果两个平行线被一条交线截断,那么所得到的内错角互补。
性质2:如果一条直线与一组平行线相交,那么所得到的同旁内错角互补。
性质3:平行线与立体图形的截线,所得到的相应角是相等的。
这些性质对于解决立体几何中的平行线问题非常有帮助,通过合理运用这些性质,可以简化解题过程,提高解题的准确性和效率。
3. 垂直线的判定及性质垂直线也是立体几何中的一个重要概念。
垂直线的判定方法有很多种,例如:相互垂直的直线斜率积为-1、垂直线上的两个向量的点积等。
我们以相互垂直的直线斜率积为-1为例进行讨论。
定理2:如果两条直线的斜率的乘积为-1,那么这两条直线相互垂直。
根据这一定理,我们可以判定两条直线是否相互垂直,进而解决立体几何中的相关问题。
4. 垂直线之间的性质在立体几何中,垂直线之间也有一些重要的性质。
下面我们来介绍其中的几个。
性质4:两条相互垂直的直线之间的角是直角。
性质5:垂直线与平行线相交所得的相应角是相等的。
这些性质同样对于解决立体几何中的垂直线问题非常有帮助。
向量法证明平行与垂直-人教版高中数学

第02讲一向量法证明平行与垂直知识图谱-利用向量证明空间中的平行关系-利用向星证明空间中的垂直关系宜线的方向向量与直线的向量方程利用向量方法证明线面平行关系利用向星方法证明线线与面面的平行关系利用向星方法证明线线垂直平面的法向星利用向星方法证明线面垂直利用向量方法证明面面垂直第02讲-向量法证明平行与垂直错题回顾利用向量证明空间中的平行关系知识Si井一・直线的方向向量与直线的向量方程1.点的位置向量在空间中,我们取一定点0作为基点,那么空间中任意一点P的位置就可以用向量成来表示,我们把向量质称为点P的位置向量.2.直线的方向向量空间中任一直线I的位置可以由I上的一个定点A以及一个定方向确定,如图,点村是直线,上的一点,向量或表示直线[的方向向量,则对于直线[上任一点户,有步弟,这样点工和向量成,不仅可以确定直线,的位置,还可具体表示出/上的任意点;直线I上的向量S以及与3共线的向量叫做i的方向向量・3.直线I的向量方程直线上任意一点P定存在实数,,使得衣=龙①,①式可以看做直线[的参数方程,直线f的参数方程还可以作如下表示:对空间中任意一确定点。
,点户在直线[上的充要条件是存在唯一的实数,满足等式灵=鬲*②,如果在,上取后=株,则上式可以化为灸=扇以刀=函硕赤-&)=(1-!)宓H房①;①②③都叫做空间直线的向量参数方程.二•平面的法向量1.平面法向量的定义已知平面a,如果向量成的基线与平面a垂直,则向量成叫作平面”的法向量或者说向量成与平面a正交.2.平面法向量的性质(1)平面“上的一个法向量垂直于平面“共面的所有向量;(2)一个平面的法向量有无限多个,它们互相平行.三.用向量方法证明空间中的平行关系1.牺平行设直线4房的方向向量分别是',5,则要证明4"《或4与"重合,只需要证明加,即M疗.2.线面平行(1)设直线,的方向向量是a,平面。
的法向量是元,要证明〃r/,只需要证明Sz;=o;(2)根据线面平行的判定定理:如果直线(平面夕卜)与平面内的一条直线平行,那么这条直线与这个平面平行;所以,要证明2直线和一个平面平行,也可以在平面内找到一个向量与已知直线的方向向量是共线向量即可;(3)根据共面向量定理可知:如果一个向量和两个不共线的向量是共面向量,那么这个向量与这两个不共面向量确定的平面一定平行.已知两个不共线向量名逡与平面“共面,一条直线]的一个方向向量为亍,则由共面向量定理,可得E或[在位内9存在两个实数W,使土戒+>£.3平行(1借能求出平面s月的法向量元足,要证明耻,只需要证明河即可.(2)由面面平行的判定定理:要证明面面平行,只要转化为相应的线面平行、线线平行即可,已知两个不共线的向量相与与平面“共面,则由两平面平行的判定与性质,得。
高中数学第3章3.2.1用向量方法解决平行与垂直问题课件新人教A选修21.ppt

(2)∵E→G=(1,-1,-1),P→G=(1,1,0), B→C=(0,-3,3), ∴E→G·P→G=1-1=0,E→G·B→C=3-3= 0, ∴EG⊥PG,EG⊥BC.
【名师点评】 证明面面垂直通常有两种方法, 一是利用面面垂直的判定定理,转化为线面垂直、 线线垂直去证明;二是证明两个平面的法向量互 相垂直.
l∥α⇔_a_⊥__u_.
面面平行
设平面α,β的法向量分别为u=(a1,b1, c1),v=(a2,b2,c2),则α∥β⇔_u_∥__v_.
3.空间中垂直关系的向量表示
空间中的垂直关系
线线垂直
线面垂直
面面垂直
设直线l的方向 设直线l的方向 设平面α的法向
向量为a=(a1, 向量为a=(a1,b1,量为u=(a1,b1,
【证明】 (1)法一:如图,以三棱锥的顶点P为 原点,以PA、PB、PC所在直线分别作为x轴、y 轴、z轴建立空间直角坐标系.令PA=PB=PC =3,则A(3,0,0)、B(0,3,0)、C(0,0,3)、E(0,2,1)、 F(0,1,0)、G(1,1,0)、P(0,0,0).
于是P→A=(3,0,0), F→G=(1,0,0), 故P→A=3F→G,∴PA∥FG. 而 PA⊥平面 PBC, ∴FG⊥平面 PBC. 又 FG⊂平面 EFG, ∴平面 EFG⊥平面 PBC.
向向量和平面的法向量间的关系证明线面平行和
面面平行.
【证明】 如图所示建立空间直角坐标系 D-xyz, 则有 D(0,0,0),A(2,0,0),C(0,2,0),C1(0,2,2), E(2,2,1),F(0,0,1),B1(2,2,2), 所以F→C1=(0,2,1), D→A=(2,0,0),A→E=(0,2,1).
人教A版选修2-1第三章学案立体几何中的空间向量方法(一)——证明垂直与平行无答案

专题:立体几何中的空间向量方法(一)——证明平行与垂直※知识要点1.直线的方向向量与平面的法向量(1)直线的方向向量:直线l 上的 向量a 或与a 的向量叫做直线l 的方向向量.(2)平面的法向量:若直线l ⊥平面α,则直线l 的 向量a 即为平面α的法向量.注意:设a ,b 是平面α内两不共线向量,n 为平面α的法向量,则求法向量的方程组为⎩⎨⎧n ·a =0,n ·b =0.2.用向量证明空间中的平行关系(1)线线平行:设直线l 1和l 2的方向向量分别为v 1和v 2,则直线l 1⊥l 2⊥ ⊥ ⊥存在实数λ,使得 ; (2)线面平行:设直线l 的方向向量为v ,与平面α共面的两个不共线向量v 1和v 2,则直线l ⊥平面α或直线l ⊥平面α⊥存在两个实数x ,y ,使得 ;(3)线面平行:设直线l 的方向向量为v ,平面α的法向量为u ,则直线l ⊥平面α或直线l ⊥平面α⊥ ; (4)面面平行:设平面α和β的法向量分别为u 1,u 2,则平面α⊥平面β⊥ . 3.用向量证明空间中的垂直关系(1)线线垂直:设直线l 1和l 2的方向向量分别为v 1和v 2,则直线l 1⊥直线l 2⊥ ⊥ ⊥ ;(2)线面垂直:设直线l 的方向向量为v ,平面α的法向量为u ,则直线l ⊥平面α⊥ ;(3)面面垂直:设平面α和β的法向量分别为u 1和u 2,则平面α⊥平面β⊥ ⊥ ⊥ . ※题型讲练【例1】已知点P 是平行四边形ABCD 所在的平面外一点,若AB →=(2,-1,-4),AD →=(4,2,0),AP →=(-1,2,-1).对于结论:①AP ⊥AB ; ②AP ⊥AD ; ③AP →是平面ABCD 的法向量; ④AP →∥BD →; 其中正确的是________. 变式训练1:1.若直线l 的方向向量为a =(1,0,2),平面α的法向量为n =(-2,0,-4),则直线l 与平面α的位置关系是________. 2.如图,正方体ABCDA 1B 1C 1D 1的棱长为1,E ,F 分别是棱BC ,DD 1上的点,如果B 1E ⊥平面ABF ,则CE 与DF 的和的值为________.【例2】如图所示,平面P AD ⊥平面ABCD ,ABCD 为正方形,△P AD 是直角三角形,且P A =AD =2,E ,F ,G 分别是线段P A ,PD ,CD 的中点.求证:PB ∥平面EFG . 变式训练2:1.如图,在四面体A -BCD 中,AD ⊥平面BCD ,BC ⊥CD ,AD =2,BD =22,M 是AD 的中点,P 是BM 的中点,点Q 在线段AC 上,且AQ =3QC .证明:PQ ∥平面BCD . 【例3】如图所示,正三棱柱(底面为正三角形的直三棱柱) ABC —A 1B 1C 1的所有棱长都为2,D 为CC 1的中点. 求证:AB 1⊥平面A 1BD . 变式训练3:1.如图,三棱锥P ABC 中,AB =AC ,D 为BC 的中点,PO ⊥平面ABC ,垂足O 落在线段AD 上.已知BC =8,PO =4,AO =3,OD =2. (1)证明:AP ⊥BC ;(2)若点M 是线段AP 上一点,且AM =3,证明:平面AMC ⊥平面BMC .【例4】如图所示,已知直三棱柱ABC —A 1B 1C 1中,⊥ABC 为等腰直角三角形,⊥BAC =90°,且AB =AA 1,D 、E 、F 分别为B 1A 、C 1C 、BC 的中点.求证: (1)DE ⊥平面ABC ; (2)B 1F ⊥平面AEF . 变式训练4:1.如图所示,在四棱锥P -ABCD 中,PC ⊥平面ABCD ,PC =2,在四边形ABCD 中,∠B =∠C =90°,AB =4,CD =1,点M 在PB 上,PB =4PM ,PB 与平面ABCD 成30°角. (1)求证:CM ∥平面P AD ; (2)求证:平面P AB ⊥平面P AD . 2.如图所示,四棱锥S —ABCD 的底面是正方形,每条侧棱的长都是底面边长的2倍,P 为侧棱SD 上的点. (1)求证:AC ⊥SD .(2)若SD ⊥平面P AC ,则侧棱SC 上是否存在一点E ,使得BE ∥平面P AC .若存在,求SE ∶EC 的值;若不存在,试说明理由. ※课后练习1.已知平面α内的三点A (0,0,1),B (0,1,0),C (1,0,0),平面β的一个法向量n=(-1,-1,-1),则不重合的两个平面α与β的位置关系是________.2.设u=(-2,2,t),v=(6,-4,4)分别是平面α,β的法向量,若α⊥β,则t等于________.3.在四棱锥P—ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E、F分别是AB、PB的中点.(1)求证:EF⊥CD;(2)在平面P AD内求一点G,使GF⊥平面PCB,并证明.4.如图,在长方体ABCD-A1B1C1D1中,AA1=AD=1,E为CD的中点.(1)求证:B1E⊥AD1;(2)在棱AA1上是否存在一点P,使得DP∥平面B1AE?若存在,求AP的长;若不存在,说明理由.5.如图,在底面是矩形的四棱锥P-ABCD中,P A⊥底面ABCD,E,F分别是PC,PD的中点,P A=AB=1,BC=2.(1)求证:EF∥平面P AB;(2)求证:平面P AD⊥平面PDC.。
高考数学总复习 97用向量方法证明平行与垂直课件 理 新人教A版

(1)AE⊥CD; (2)PD⊥平面 ABE.
证明:∵AB、AD、AP 两两垂直,建立如图所示的空间 直角坐标系,
设 PA=AB=BC=1,则 P(0,0,1).
(1)∵∠ABC=60°, ∴△ABC 为正三角形. ∴C(12, 23,0),E(14, 43,12). 设 D(0,y,0),由 AC⊥CD, 得A→C·C→D=0, ∴y=233,即 D(0,233,0), ∴C→D=(-12, 63,0).
(2)证明直线 l∥平面 α 时,
①可取直线 l 的方向向量 a 与平面 α 的法向量 n,证明 a·n =0;
②可在平面 α 内取基向量{e1,e2},证明直线 l 的方向向 量 a=λ1e1+λ2e2,然后说明 l 不在平面 α 内即可;
③在平面 α 内找两点 A、B,证明直线 l 的方向向量 n∥A→B.
又A→E=(14, 43,12), ∴A→E·C→D=-12×14+ 63× 43=0, ∴A→E⊥C→D,即 AE⊥CD.
(2)设平面 ABE 的一个法向量为 n=(x,y,z), ∵A→B=(1,0,0),A→E=(14, 43,12),
∴nn··AA→ →BE= =00, ,
x=0, 即14x+ 43y+12z=0.
考点典例讲练
用向量证明线面平行 [例 1] 如图所示,平面 PAD⊥平面 ABCD,四边形 ABCD 为正方形,△PAD 是直角三角形,且 PA=AD=2,E、F、G
分别是线段 PA、PD、CD 的中点.求证:PB∥平面 EFG.
分析:欲证线面平行,可考虑找出平面 EFG 的一个法向 量 n,证明P→B·n=0,也可以考虑将P→B用平面 EFG 内两不共 线向量线性表示,由于四边形 ABCD 为正方形,平面 PAD⊥ 平面 ABCD,PA⊥AD,故可建立空间直角坐标系,用向量的 坐标运算证明.
人教版湖南省长沙市长郡中学2020-2021学年度上学期高二数学《空间向量与平行_垂直关系》教育课件

跟踪训练 3 在四棱锥 S-ABCD 中,底面 ABCD 是正方 形,AS⊥底面 ABCD,且 AS=AB,E 是 SC 的中点.求证:平 面 BDE⊥平面 ABCD.
课堂小结
1.向量法处理平行、垂直问题 2.向量法证明空间几何问题的两种基本思路 思路一:用向量表示几何量,利用向量的运算进行判断. 思路二:用向量的坐标表示几何量.
直线与平面
l1∥l2⇔v1∥v2⇔v1=
λv2(λ 为非零实数)
①l∥α⇔v⊥n1⇔v·n1
=0
l1⊥l2⇔v1⊥v2⇔v1·v2 =0
(v 为直线 l 的方向 ②l∥α⇔v=xa+yb, l⊥α⇔v∥n1⇔v=λn1(λ
向量,n1 为平面 α 其中 a,b 为平面 α 内不
为非零实数)
的法向量) 共线的向量,x,y 均为
心
安
;
书
一
笔
清
远
,
盈
一
抹
恬
淡
,
浮
华
三
千
,
只
做
自
己
;
人
间
有
情
,
心
中
有
爱
,
携
一
米
阳
光
,
微
笑
向
暖
。
口
罗
不
是
。
■
电
:
那
你
的
第
一
部
戏
有
没
有
胆
怯
,
像
费
里
尼
拍
第
一
部
戏
时
就
穿
戴
人教A版选修2-1第三章学案立体几何中的空间向量方法(一)——证明垂直与平行无答案

专题:立体几何中的空间向量方法(一)——证明平行与垂直※知识要点1.直线的方向向量与平面的法向量(1)直线的方向向量:直线l 上的 向量a 或与a 的向量叫做直线l 的方向向量.(2)平面的法向量:若直线l ⊥平面α,则直线l 的 向量a 即为平面α的法向量.注意:设a ,b 是平面α内两不共线向量,n 为平面α的法向量,则求法向量的方程组为⎩⎨⎧n ·a =0,n ·b =0.2.用向量证明空间中的平行关系(1)线线平行:设直线l 1和l 2的方向向量分别为v 1和v 2,则直线l 1∥l 2⇔ ∥ ⇔存在实数λ,使得 ; (2)线面平行:设直线l 的方向向量为v ,与平面α共面的两个不共线向量v 1和v 2,则直线l ∥平面α或直线l ⊂平面α⇔存在两个实数x ,y ,使得 ;(3)线面平行:设直线l 的方向向量为v ,平面α的法向量为u ,则直线l ∥平面α或直线l ⊂平面α⇔ ; (4)面面平行:设平面α和β的法向量分别为u 1,u 2,则平面α∥平面β⇔ . 3.用向量证明空间中的垂直关系(1)线线垂直:设直线l 1和l 2的方向向量分别为v 1和v 2,则直线l 1⊥直线l 2⇔ ⊥ ⇔ ;(2)线面垂直:设直线l 的方向向量为v ,平面α的法向量为u ,则直线l ⊥平面α⇔ ;(3)面面垂直:设平面α和β的法向量分别为u 1和u 2,则平面α⊥平面β⇔ ⊥ ⇔ . ※题型讲练【例1】已知点P 是平行四边形ABCD 所在的平面外一点,若AB →=(2,-1,-4),AD →=(4,2,0),AP →=(-1,2,-1).对于结论:①AP ⊥AB ; ②AP ⊥AD ; ③AP →是平面ABCD 的法向量; ④AP →∥BD →; 其中正确的是________.变式训练1:1.若直线l 的方向向量为a =(1,0,2),平面α的法向量为n =(-2,0,-4),则直线l 与平面α的位置关系是________.2.如图,正方体ABCDA 1B 1C 1D 1的棱长为1,E ,F 分别是棱BC ,DD 1上的点,如果B 1E ⊥平面ABF ,则CE 与DF 的和的值为________.【例2】如图所示,平面P AD ⊥平面ABCD ,ABCD 为正方形,△P AD 是直角三角形,且P A =AD =2,E ,F ,G 分别是线段P A ,PD ,CD 的中点.求证:PB ∥平面EFG .变式训练2:1.如图,在四面体A -BCD 中,AD ⊥平面BCD ,BC ⊥CD ,AD =2,BD =22,M 是AD的中点,P 是BM 的中点,点Q 在线段AC 上,且AQ =3QC .证明:PQ ∥平面BCD .【例3】如图所示,正三棱柱(底面为正三角形的直三棱柱)ABC—A1B1C1的所有棱长都为2,D为CC1的中点.求证:AB1⊥平面A1BD.变式训练3:1.如图,三棱锥P ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上.已知BC=8,PO=4,AO=3,OD=2.(1)证明:AP⊥BC;(2)若点M是线段AP上一点,且AM=3,证明:平面AMC⊥平面BMC. 【例4】如图所示,已知直三棱柱ABC—A1B1C1中,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,D、E、F分别为B1A、C1C、BC的中点.求证:(1)DE∥平面ABC;(2)B1F⊥平面AEF.变式训练4:1.如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC =2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°角.(1)求证:CM∥平面P AD;(2)求证:平面P AB⊥平面P AD.2.如图所示,四棱锥S—ABCD的底面是正方形,每条侧棱的长都是底面边长的2倍,P为侧棱SD上的点.(1)求证:AC⊥SD.(2)若SD⊥平面P AC,则侧棱SC上是否存在一点E,使得BE∥平面P AC.若存在,求SE∶EC的值;若不存在,试说明理由.※课后练习1.已知平面α内的三点A(0,0,1),B(0,1,0),C(1,0,0),平面β的一个法向量n=(-1,-1,-1),则不重合的两个平面α与β的位置关系是________.2.设u=(-2,2,t),v=(6,-4,4)分别是平面α,β的法向量,若α⊥β,则t等于________.3.在四棱锥P—ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E、F分别是AB、PB的中点.(1)求证:EF⊥CD;(2)在平面P AD内求一点G,使GF⊥平面PCB,并证明.4.如图,在长方体ABCD-A1B1C1D1中,AA1=AD=1,E为CD的中点.(1)求证:B1E⊥AD1;(2)在棱AA1上是否存在一点P,使得DP∥平面B1AE?若存在,求AP的长;若不存在,说明理由.5.如图,在底面是矩形的四棱锥P-ABCD中,P A⊥底面ABCD,E,F分别是PC,PD的中点,P A=AB=1,BC=2.(1)求证:EF∥平面P AB;(2)求证:平面P AD⊥平面PDC.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.3 向量的平行和垂直
例1.已知向量y x DA BC CD y x BC AB ,,//),3,2(),,(),1,6(求实数时当向量--===应满足的条件. 例2.已知.|,|||垂直与证明b a b a b a -+=
例3.设已知点O (0,0),A (1,2),B (4,5)及.AB t OA OP += 求(1)t 为何值时,P 在x 轴上?P 在y 轴上?P 在第二象限? (2)四边形OABP 能否成为平行四边形?证明你的结论. 例4.求证ΔABC 的三条高相交于一点. 【备用题】
已知).()(:,,0,0b a b a b a b a -+≠≠不平行于求证不平行于 【基础训练】
1.与向量)4,3(-=a 垂直的单位向量是______________. 2.与向量)4,3(-=平行的单位向量是______________.
3.若D B A e e CD e e CB e k e AB e e ,,,2,3,2,,21212121若已知是两个不共线的向量-=+=+=三点共线, 则k =______________.
4.若的是则y y
x x y x y x //),,(),,(2
1212211=== ( )
A .充要条件
B .充分非必要条件
C .必要非充分条件
D .既非充分又非必要条件 5.如果)4,1()3,22(++=--=x x b x a 与互相垂直,则实数x 等于 ( )
A .
2
1
B .
2
7
C .
21或2
7
D .
2
7
或-2 6.给出下列命题:
(1)如果;)0(=≠=那么λλλ (2)如果;),0(b a c c b c a =≠⋅=⋅那么 (3)如果;,0⊥=⋅那么
(4)如果b a b a b a 与那么,0||||≠⋅-=⋅方向相反;
(5)如果b a b a 与那么,0<⋅的夹角为钝角. 其中假命题是____________(将假命题的序号都填上) 【拓展练习】
1.三点A(x 1,y 1),B(x 2,y 2),C(x 3,y 3)共线的充要条件是 ( ) A .x 1y 2-x 2 y 1=0 B .x 1 y 3-x 3 y 1=0 C .))(())((12131312y y x x y y x x --=-- D .))(())((13121312y y y y x x x x --=-- 2的三个顶点为A(-1,-2),B(3,-1),C(5,6),则顶点D 的坐标为________.
3.已知为则且⋅==,2||,1||//
( )
A .2
B .-2
C .±2
D .±3
4.非零向量、-+=与则向量不平行于且满足,|,|||的位置关系是 ( )
A .平行
B .垂直
C .共线且同向
D .共线且反向 5.下列命题中正确的是 ( )
A .若0,0==⋅b a b a 或则
B .若b a b a //,0则=⋅
C .若2)(,⋅=⋅⊥则
D .若||||,,=⋅则共线
6.已知=-⊥-=+=k b a a j i b kj i a 则且),(,24,2____________.
7.已知.//,_________,,__________),3,4(),7,(x x x x 时当时当===+==
8.设命题:p :向量的是则使得有且只有一个实数命题共线与q p a b q a b ,,:,λλ= ( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分又不必要条件 9.下面四个条件:)0(),(0532121≠∈=∈=+=-=+b R b a R x x b x a x e b a e b a 且唯一且③②且①λλλ )0,(0=+∈=+y x R y x 且④其中能使与共线的是
( )
A .①②
B .①③
C .②④
D .③④
10.已知在梯形ABCD 中,.),2//(),7,3(),2,3(),1,1(,//点坐标求若D AB BD AD C B A CD AB ----
11.已知、.||||:,-=+⊥求证是非零向量
12.已知:C 是以AB 为直径的半圆上任意一点,求证:.BC AC ⊥
13.已知平面内三个点A (1,7),B (0,0),C (8,3),D 为线段BC 上一点,且
D BC DA CA BA 求,)(⊥++点坐标.。
