平曲线视距横净距的计算
公路平曲线坐标计算公式

Goto 0
注:K:欲求点里程
O:圆曲线起点里程
C:圆曲线起点X坐标
R:圆曲线半径(左偏为负)
Q:起始方位角
D:距中桩的距离
S:斜交角度
F:圆曲线起点Y坐标
3、直线
Lb10
{K,D}
①L=K-0
②X=C+LcosQ+Dcos(Q+S)◢
⑥I=(L2-T2)*180/2/A2/π
⑦X=C+Mcos(Q-ZB)-ZNsin(Q-ZB)+Dcon(Q+ZI+S)◢
⑧Y=F+Msin(Q-ZB)+ZNcos(Q-ZB)+Dsin(Q+ZI+S)◢
Goto 0
注:A:缘和曲线参数
R:起点半径
J:曲率半径判定值(当曲率半径由小到大取1,否则取-1)(当起点半径到终点半径是由大或无穷大到小取+1,反之则取-1)
T:切线长
M:顶点高程
I:坡度
Z:竖曲线判定值
三、预拱度计算公式
Lb1 0
①{K}
②H=D-(4D÷B2)×(B/2-(K-O))2◢
Goto 0
注:D:跨中最大设计预拱度
H:要计算的预拱度
K:欲求点里程桩号(距支座的距离)
O:起点桩号
B:本跨净长
③Y=F+LsinQ+Dsin(Q+S)◢
Goto 0
注:K:欲求点里程
O:直线起点里程
C:直线起点X坐标
Q:起始方位角
第五章道路勘测设计横断面设计54、55介绍

(第五章 横断面设计:4、5节)
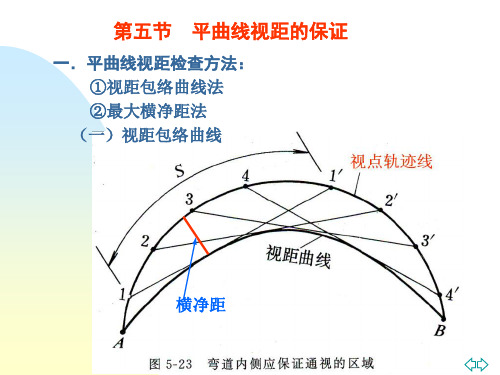
第四节 平曲线视距的保证
一.平曲线视距检查方法: ① 视距包络曲线法 ② 最大横净距法
(一)视距包络曲线
横净距
(二)最大横净距及其计算 横净距:在弯道各点的横断面上,驾驶员视点轨迹线与视距线之间
的最大距离叫横净距。 S
h B
A
横净距:在弯道各点的横断面上,内侧车道中线行车轨迹与视距线 之间的最大距离叫横净距。
1.平曲线资料:半径、缓和曲线、偏角、曲线位置(交点桩号) 等;
2.每个中桩的填挖高度; 3.路基宽度,路面宽度(分别确定左右侧宽度); 4.各中桩的超高值; 5.路基标准横断面图式(典型横断面 ); 6.路基边坡坡度值; 7.边沟、截水沟的形式及尺寸; 8.弯道上视距的是否得到保证(视距台设计)。
(三)横断面图绘制方法
1.在计算纸上绘制横断面的地面线。 地面线是在现场测绘的,若是纸上定线,可从大比例尺的地形 图上内插获得。 横断面图的比例尺一般是1:200。 2.绘出设计线:“戴帽子”
K5+300.00 2.52
K5+300.00 右:3.7, -.17, 12.7, -1.07, 25, -2.31 左:6.4, 0.82, 8.7, 1.3, 13.58,1.79, 25, 2.87
(三)坐标法
已知断面图上各转折点坐标(,),则断面面积为:
F1 2
arc{tlg[1l'(l')2]}
6RS l l
l'12(Ls S)
(3)曲线总长L<S:
h aR s r( c1 t gc l o 2 2 s ) ls2 i n ) (S 2 L ss2 in 6RS
平曲线的五大要素计算公式

平曲线的五大要素计算公式以下是关于平曲线的五大要素计算公式。
平曲线是指在平面上描述一条曲线的五种基本参数,包括曲线长度、曲线半径、曲线角度、曲线切线和曲线弧度。
下面是这五种要素的计算公式:1.曲线长度(L):曲线长度可以通过计算曲线上的所有坐标点之间的距离来获得。
对于参数方程表示的曲线,曲线长度L可以通过以下公式计算: L=∫(√((dx/dt)²+(dy/dt)²)dt) 其中,(dx/dt)和(dy/dt)分别是曲线在x和y方向上的速度矢量。
2.曲线半径(R):曲线半径表示曲线在某一点处弯曲的程度。
对于圆弧曲线,曲线半径R可以通过以下公式计算: R=(dx²+dy ²)^(1/2)/(1+(dy/dx)²)^(1/2) 其中,(dx,dy)是曲线上的某一点坐标。
3.曲线角度(θ):曲线角度表示曲线在某一点处与x轴的夹角。
对于参数方程表示的曲线,曲线角度θ可以通过以下公式计算: θ=atan2(dy/dx) 其中,(dx,dy)是曲线上的某一点坐标。
4.曲线切线(T):曲线切线表示曲线在某一点处的切线方向。
对于参数方程表示的曲线,曲线切线T可以通过以下公式计算: T=(dx/dt,dy/dt) 其中,(dx/dt)和(dy/dt)分别是曲线在x和y方向上的速度矢量。
5.曲线弧度(α):曲线弧度表示曲线在某一点处沿逆时针方向的旋转程度。
对于圆弧曲线,曲线弧度α可以通过以下公式计算: α=θ 其中,θ是曲线在某一点处与x轴的夹角。
需要注意的是,这些公式适用于平曲线的一般情况。
在实际应用中,根据具体的曲线类型和表示方式,可能需要对公式进行相应的调整。
平曲线视距
(三)横断面施工图
跳转到第一页
作业: 已知某点路基宽度为12m,填挖高度4.12m,路基边 坡为1:1.5,试绘出该断面的横断面图。该点横断面 地面线实测资料如下: K5+300.00 右:3.7,-.17,12.7,-1.07,25,-2.31 左:6.4,0.82,8.7,1.3,13.58,1.79,25,2.87
h
跳转到第一页
最大横净距计算方法:
2.设回旋线的横净距计算:
(1)圆曲线长L'>S:
h
Rs
(1
cos
2
)
跳转到第一页
最大横净距计算方法:
2.设回旋线的横净距计算:
(1)圆曲线长L'>S:
h
Rs
(1
cos
2
)
(2)曲线总长L>S>L'
h
Rs
(1
cos
2
2
)
(l
l')
sin(
跳转到第一页
跳转到第一页
(三)横断面图绘制方法
1.在计算纸上绘制横断面的地面线。 地面线是在现场测绘的,若是纸上定线,可从大比例尺的地 形图上内插获得。 横断面图的比例尺一般是1:200。 2.绘出设计线:“戴帽子”
K5+300.00 T=2.52
K5+300.00 右:3.7, -.17, 12.7, -1.07, 25, -2.31 左:6.4, 0.82, 8.7, 1.3, 13.58,1.79, 2跳转5到,第一2页.87
导线测量常用计算公式

导线测量常用计算公式导线测量是土木工程或电气工程中的一项重要工作,主要用于确定建筑物的位置、土地边界以及计算地形的变化等。
在导线测量中,有很多常用的计算公式可以帮助工程师或测量师进行精确的测量和计算。
以下是一些常用的导线测量计算公式:1.距离计算公式:-垂直平距(垂距):D=SQRT((ΔN)^2+(ΔE)^2)-水平平距:H=SQRT((ΔN)^2+(ΔE)^2+(ΔH)^2)-斜距:L=SQRT((ΔN)^2+(ΔE)^2+(ΔH)^2)- 仰角:A = arctan(ΔH / H)-前视高差:h1=H1-H0-反视高差:h2=H0-H22.坐标计算公式:- 相对平差量:ΔX = (ΔN * cosα) + (ΔE * sinα)- 相对平差量:ΔY = (ΔN * sinα) - (ΔE * cosα)-新坐标X=X0+∑(ΔX)-新坐标Y=Y0+∑(ΔY)3.角度计算公式:- 方位角:I = arctan((ΔE2 - ΔE1) / (ΔN2 - ΔN1))-转角:θ=I2-I1-内角和:∑θ=∑(Ii)-外角和:∑θ=n*180°-∑(Ii)4.高程计算公式:-平均高程:H=(H0+H1+H2)/3-高程改正:ΔHi=Hi-H-净高差:Nh=h1+ΔH5.线性状况计算公式:-输沙率:Q=W/(T*B)其中,Q为输沙率,W为沙子的质量,T为时间,B为河道截面积。
6.面积计算公式:-梯形法计算面积:A={0.5*(a+b)*h}- 辛普森法计算面积:A = {h / 3 * (y0 + 4y1 + 2y2 + 4y3 + ... + yn)}7.建筑斜率计算公式:-百分比斜率:P=(ΔH/L)*100- 度数斜率:s = tan^-1(ΔH / L)这些计算公式是导线测量中常用的工具,可以帮助工程师或测量师在实际工作中准确地计算测量结果。
需要根据具体的测量需求和情况选择合适的公式进行计算,并注意测量文档中的单位和精度要求,以确保测量结果的准确性。
平曲线要素计算公式(给学生用的)

精心整理第三节竖曲线纵断面上两个坡段的转折处,为方便行车,用一段曲线来缓和,称为竖曲线采用抛物线拟合。
一、竖曲线要素的计算公式相邻坡段的坡度为i 1和i 2,代数差为ω=i 2-i 1ω为正时,是凹曲线;ω为负,是凸曲线。
2.竖曲线诸要素计算公式竖曲线长度或竖曲线半径R:(前提:ω很小)L=R ω竖曲线切线长:T=L/2=R ω/2竖曲线上任一点竖距h :(2)曲线主点桩号计算:ZH(桩号)=JD(桩号)-THY(桩号)=ZH(桩号)+l sQZ(桩号)=HZ(桩号)-L/2YH(桩号)=HY(桩号)+L yHZ(桩号)=YH(桩号)+l sJD(桩号)=QZ(桩号)+J/230-3 336629-3 4028)-(3 )(227-3 2sec )(26-3 225-3 2ls 180)2(m 18024)-(3 2)(23)-(3 9022)-(3 23842421)-(3 )( 240234202300034223m Rl R l y m Rl l x m L T J m R p R E m l L L R l R L m q tg p R T R l m R l R l p m R l l q s s s s s Y s s s s s s -=-=-=-⋅+=-=+⋅⋅-=+⋅⋅=+⋅+=︒⋅︒=-=-=απβααπαπβ竖曲线外距:[例1]、某山岭区二级公路,变坡点桩号为K5+030.00,标高为427.68m,变坡点桩号的地面高程为450.65m,i1=+5%,i2=-4%,竖曲线半径R=2000m。
试计算竖曲线诸要素以及桩号为K5+000.00和K5+100.00处的设计高程,BPD 的设计高程与施工高。
解:1.计算竖曲线要素ω=|i2-i1|=|-0.04-0.05|=0.09,为凸型。
曲线长L=Rω=2000×0.09=180m切线长T=L/2=180/2=90m外距E=T2/2R=902/2×2000=2.03m2.计算设计高程竖曲线起点桩号=(K5+030.00)-90=K4+940.00竖曲线起点高程=427.68-90×0.05=423.18竖曲线终点桩号=(K5+030.00)+90=K5+120.00竖曲线终点高程=427.68-90×0.04=424.08桩号K5+000.00处:横距K5x1=(K5+000.00)-(K4+940.00)=60m竖距h1=x12/2R=602/2×2000=0.90m切线高程=427.68-(90-60)×0.05=426.18m423.18+60×0.05=426.18设计高程=426.18-0.90=425.28m桩号K5+100.00处:横距x2=(K5+120.00)-(K5+100.00)=20m竖距h2=x22/2R=202/2×2000=0.1m切线高程=427.68-(90-20)×0.04=424.88m设计高程=424.88-0.1=424.78m横距x2=(K5+100.00)-(K4+940.00)=160m竖距h2=x22/2R=1602/2×2000=6.4m切线高程=423.18+160×0.05=431.18m设计高程=431.18-6.40=424.78mBPD设计高程=427.68-E=425.65mBPD施工高=设计高程-地面高程=425.65-450.65=-25m,应为挖方。
平曲线计算公式

平曲线计算公式摘要:一、引言二、平曲线计算公式简介1.什么是平曲线2.平曲线计算公式的意义三、平曲线计算公式推导1.圆曲线计算公式2.缓和曲线计算公式四、平曲线计算公式应用1.在道路设计中的应用2.在其他领域中的应用五、结论正文:一、引言在我国的土木工程领域,平曲线计算公式是道路设计中一个重要的计算工具。
它可以帮助工程师们快速、准确地计算道路的平曲线,从而为道路的设计和施工提供科学依据。
本文将对平曲线计算公式进行详细介绍,包括公式的推导和应用。
二、平曲线计算公式简介1.什么是平曲线平曲线,又称平曲线段,是指道路在水平方向上连续变化的曲线。
它可以使车辆在行驶过程中,不断地改变行驶方向,从而有效地减少行驶距离和行驶时间。
平曲线的形状有很多种,如圆曲线、缓和曲线等。
2.平曲线计算公式的意义平曲线计算公式是一种计算平曲线长、距等参数的公式。
通过使用这些公式,工程师们可以快速、准确地计算出道路的平曲线,为道路的设计和施工提供科学依据。
三、平曲线计算公式推导1.圆曲线计算公式圆曲线是由一个半径相等的圆所组成的平曲线。
它的计算公式如下:L = πr + 2r * arcsin(ΔL/2r)其中,L表示圆曲线长,r表示圆曲线半径,ΔL表示圆曲线长度的变化。
2.缓和曲线计算公式缓和曲线是一种逐渐变化的平曲线,它由多个圆曲线组成。
它的计算公式如下:L = nπr + (n-1) * 2r * arcsin(ΔL/2r)其中,L表示缓和曲线长,r表示缓和曲线半径,n表示缓和曲线的圆曲线个数,ΔL表示缓和曲线长度的变化。
四、平曲线计算公式应用1.在道路设计中的应用平曲线计算公式在道路设计中的应用十分广泛。
例如,在道路的选线、定线、设计等方面,工程师们需要根据道路的地形、地质、交通量等因素,选择合适的平曲线,并计算出平曲线的长度、距等参数。
这都需要用到平曲线计算公式。
2.在其他领域中的应用除了道路设计外,平曲线计算公式在其他领域也有广泛的应用。
平曲线计算公式

平曲线计算公式(原创版)目录1.引言2.平曲线计算公式的定义与分类3.平曲线计算公式的应用4.平曲线计算公式的优缺点5.结论正文1.引言平曲线是道路工程中常见的一种曲线形式,它是指在道路的纵断面上,道路中心线在水平方向上呈平滑变化的曲线。
平曲线的计算对于道路的设计与施工具有重要意义,而平曲线计算公式则是实现这一目标的关键工具。
本文将详细介绍平曲线计算公式的定义与分类、应用、优缺点等方面的内容。
2.平曲线计算公式的定义与分类平曲线计算公式是指在道路工程中,用来计算道路中心线在纵断面上呈平滑变化的曲线公式。
根据计算方法的不同,平曲线计算公式可以分为以下几类:(1)基于矢量的计算公式:这类公式主要利用矢量的运算来计算平曲线,如计算曲线的曲率、切线角等。
(2)基于参数的计算公式:这类公式主要通过参数方程来描述平曲线,如用弧长、半径等参数来表示曲线。
(3)基于几何图形的计算公式:这类公式主要通过几何图形的性质来计算平曲线,如通过椭圆、抛物线等几何图形来表示曲线。
3.平曲线计算公式的应用平曲线计算公式在道路工程中有广泛的应用,主要包括以下几个方面:(1)道路设计:通过计算平曲线,可以得到道路中心线在纵断面上的形状,从而满足道路的安全、舒适、经济等设计要求。
(2)道路施工:在道路施工过程中,需要根据平曲线计算公式来控制道路中心线的形状,以保证道路的施工质量。
(3)道路维护:在道路维护过程中,通过对平曲线的计算与分析,可以及时发现道路的不良状况,为道路的维护提供依据。
4.平曲线计算公式的优缺点平曲线计算公式具有以下优点:(1)计算简便:平曲线计算公式具有明确的计算步骤和简单的计算方法,便于工程技术人员掌握和使用。
(2)适用性强:平曲线计算公式适用于各种类型的道路,无论是直线、曲线还是复合曲线,都可以采用相应的公式进行计算。
然而,平曲线计算公式也存在一定的缺点:(1)计算精度受限:由于公式本身的局限性,平曲线计算公式的计算精度受到一定的限制,可能无法满足某些高精度计算的需求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平曲线视距横净距的计算发表人:王乃坤江树华单位:龙建路桥股份有限公司第二工程处日期:二OO四年十二月十五三十日平曲线视距横净距的计算王乃坤江树华(龙建路桥股份有限公司第二工程处)提要:本文介绍用计算机计算平曲线及相邻直线段上任一点的横净距的方法。
关键词:平曲线横净距计算机计算CalculatingabouttheCrossClearanceDistanceofHorizontalCurveStadiaWANGNai-kunJIANGShu-huaQUZhi-chengAbstract:Calculatingmethodofhorizontalcurveandcrossclearancedistancewithcomputerispresented.Keywords:HorizontalcurveCrossclearancedistanceComputer1前言如何准确计算平曲线及相邻直线段上任一点的横净距,是我们工程技术人员在实际工作中常遇到的问题。
近期我们成功地利用计算机程序解决了带缓和曲线的平曲线横净距计算,省时省力,起到了事半功倍的效果。
现介绍如下,仅供参考。
2横净距的计算方法2.1计算原理如图1所示,某交点转角为α,平曲线半径为R1,缓和曲线长为Ls1(我们将圆曲线作为Ls1=0的特例处理)。
若行车道宽度为b,则计算横净距时的行车轨迹线(距未加宽时的行车道内侧边缘1.5m,图中虚曲线所示)与路中线的径向间距△R=b/2-1.5。
M为平曲线和相邻直线段上的任一点,M所在断面的横净距可按下法计算:在M点的法线MN两侧的行车轨迹线上分别找一点A、B,使A、B两点间沿行车轨迹线的长度等于设计视距S,计算AB连线与MN的交点E到M点的距离值H;保持A、B两点间沿行车轨迹线的长度不变,使A、B两点沿行车轨迹线同步移动时,H 值也随之改变,最大的H值与△R之差即为M点的横净距。
2.2行车轨迹线参数的确定对于半径为R1、缓和曲线长度为L S1的平曲线,行车轨迹线上对应的曲线半径R2=R1-△R,对应的缓和曲线长度L S2应是多少呢?我们分别用p、q、E、T表示圆曲线设置缓和曲线后的内移值、切垂距、外距、切线长,并分别用下标1、2对路中线、行车轨迹线上有关的量进行的区分。
如图2所示,因路中线与行车轨迹线的径向间距为△R,则应有:图二将有关各量代入并整理后可得:在R1R2L S1是定值的情况下,使△p、△q同时等于零是不可能的(L S1=0时除外)。
也就是说,无论L S2取何值,由R2L S2确定的轨迹线(下文中称之为计算行车轨迹线)与理论行车轨迹线(距未加宽时的行车道内侧边缘1.5m)不可能完全重合,两轨迹线间的偏离程度可表示为:将有关各量代入并整理后可得:上式中,△E表示计算行车轨迹线与理论行车轨迹线的曲线中点间的距离,△T表示两轨迹线上的曲线起(终)点沿切线方向的距离。
既然计算行车轨迹线与理论行车轨迹线不能完全重合,那么我们能否选取适当的L S2值,使两轨迹线尽量接近,从而满足横净距计算的精度要求呢?由(1)、(2)式可以看出,△p对两轨迹线间偏离程度的影响远比△q的影响大,如果我们通过L S2的取值使△p等于零,即用牛顿迭代法按下式解算L S2此外,两迹线的偏离程度可表示为:△E=0△T=△q两轨迹线在圆曲线段重合,下面我们来看看两轨迹线在缓和曲线段的偏离情况。
? 如图3所示,A为路中线上缓和曲线段内的任一点,距缓和曲线起点ZH1的长度为L1,在xoy 坐标系中的坐标为(X A,Y A),A点的法线AF与x轴的夹角为:沿法线AF由A点向曲线内侧移动△R得B点,则B点的坐标为:由路中线与理论行车轨迹线的关系知:B点在理论行车轨迹线上。
令C点为计算行车轨迹线上缓和曲线段内一点,距缓和曲线段起点ZH2的长度为L2,在x'o'y'坐标系中的坐标为(x'c,y'c),经坐标轴平移后可得C点在xoy坐标系中的坐标:若X c=X b,则(Y c-Y b)cos(γ-π/2)即可视为该位置处计算行车轨迹线与理论行车轨迹线间的径向偏离值。
按上述方法,我们用计算机对《公路曲线测设用表》(第二册)中“缓和曲线长度总表”列出的R1、Ls1的所有组合进行了有关计算。
计算结果表明:计算行车轨迹线与理论行车轨迹线在缓和曲线段的径向偏离值有以下特点:(1)两轨迹线在缓和曲线段中部的偏离值最大,向两端逐渐趋于零;(2)Ls1值不变时,R1值愈小,两轨迹线在缓和曲线段的偏离值就愈大;(3)R1值不变时,Ls1愈大,两轨迹线在缓和曲线段的偏离值就愈大;(4)表列各种组合中,两轨迹线在缓和曲线段的最大偏离值一般均小于0.01m,最大偏离值超过0.01m的组合只有以下4个:①R1=65、Ls1=60、b=7.5时,最大偏离值为0.015m;②R1=60、Ls1=60、b=7.5时,最大偏离值为0.018m;③R1=35、Ls1=35、b=6时,最大偏离值为0.012m;④R1=30、Ls1=35、b=6时,最大偏离值为0.016m。
通过对两轨迹线间偏离值的计算可知:由R2=R1-△R和按(3)式解算的Ls2确定的计算行车轨迹线与理论行车轨迹线非常接近(Ls1=0时两轨迹线重合),若用计算行车轨迹线代替理论行车轨迹线来计算横净距,最大误差不会超过0.02m,完全能够满足横净距计算的精度要求。
2.3横净距的计算为方便计算,我们也用桩号表示行车轨迹线上各点间的相对位置关系,并假定行车轨迹线上曲线起点ZH2(ZY2)与路中线上曲线起点ZH1(ZY1)的桩号相同(两线上的桩号是相互独立的)。
这样对于任一给定的桩号,能且只能在行车轨迹线上找到一点与之对应。
如图1,欲求横净距的断面M的桩号为L0,我们不妨先假设行车轨迹线上视距起终点A、B的桩号分别为L0-S/2、L0+S/2(在应用范围内,A、B不会落在法线MN的同一则),此时沿行车轨迹线A、B间的长度等于设计视距S,计算AB与MN的交点到M点的距离值H;然后将A、B两点沿行车轨迹线向前移动0.01m,即A、B点的桩号同时增大0.01m,再计算MN与新直线AB的交点到M点的距离值H。
根据两次计算的距离值H的大小,使A、B向距离值H增大的方向同步等量逐渐移动(以保证沿行车轨迹线A、B间的长度恒等于设计视距S)直到距离值H开始减小为止,此时的距离值H与△R之差即为M点的横净距。
按上述方法,我们编写了计算横净距的程序。
3实例应用鹤大公路鸡牡段林口支线为山岭区三级公路,行车道宽6m,设计视距(二倍停车视距)S=60m;JD2转角α=76°32′,曲线半径100m,缓和曲线长Ls=25m,曲线起点桩号为K2+838.68,计算各有关断面的横净距。
程序运行时的操作及计算结果如下(带下画线者为输入的数据):曲线起点桩号?838.68转角:?76°?32′?0〃平曲线半径?100缓和曲线长?25行车道宽度?6设计视距?60曲线主点桩号:ZH=838.68HY=863.68QZ=917.97YH=972.26HZ=997.26断面桩号(<0结束)?800横净距:0.00断面桩号(<0结束)?820横净距:0.34断面桩号(<0结束)?838.68横净距:1.41断面桩号(<0结束)?840横净距:1.53断面桩号(<0结束)?860横净距:3.52断面桩号(<0结束)?863.68横净距:3.80断面桩号(<0结束)?880横净距:4.45断面桩号(<0结束)?900横净距:4.53断面桩号(<0结束)?917.97横净距:4.53断面桩号(<0结束)?920横净距:4.53断面桩号(<0结束)?940横净距:4.53断面桩号(<0结束)?960横净距:4.37断面桩号(<0结束)?980横净距:3.14断面桩号(<0结束)?997.26横净距:1.41断面桩号(<0结束)?1000横净距:1.19断面桩号(<0结束)?1020横净距:0.23断面桩号(<0结束)?1040横净距:0.00断面桩号(<0结束)?-1OK4源程序10CLEAR:DEFDBLA-H,20CLS:LOCATE11,1:INPUT〃曲线起点桩号:〃;ZH130PRINT〃转角:40LOCATE12,6:INPUTZJ1:LOCATE12,14:INPUTZJ2:LOCATE12,22:INPUTZJ3 50INPUT〃平曲线半径=〃;R1:INPUT〃缓和曲线长=〃;LS160INPUT〃平曲线半径=〃;LMK:INPUT〃设计视距=〃;S70ZJ=(ZJ1+ZJ2/60+ZJ3/3600)*PI/180:DR=LMK/2-1.5:R2=R1-DR80IFLS1>0THENGOSUB640:REM计算LS290R=R1:LS=LS1:GOSUB710:LY1=LY:P1=P:Q1=Q:T1=T100R=R2:LS=LS2:GOSUB710:LY2=LY:P2=P:Q2=Q:T2=T110DT=Q1-Q2:ZH2=ZH1:SS=S/2/R2*R1120HY1=ZH1+LS1:YH1=HY1+LY1:HZ1=YH1+LS1:QZ1=(ZH1+HZ1)/2130HY2=ZH2+LS2:YH1=HY2+LY2:HZ2=YH2+LS2:QZ2=(ZH2+HZ2)/2140PRINT〃曲线主点桩号:〃:A$=〃######.##〃:IFLS1=0THEN180150PRINT〃ZH=〃;USINGA$;ZH1:PRINT〃HY=〃;USINGA$;HY1160PRINT〃QZ=〃;USINGA$;QZ1:PRINT〃YH=〃;USINGA$;YH1170PRINT〃HZ=〃;USINGA$;HZ1:GOTO200180PRINT〃ZY=〃;USINGA$;ZH1:PRINT〃QZ=〃;USINGA$;QZ1190PRINT〃YZ=〃;UXINGA$;HZ1200INPUT〃断面桩号(<0结束)〃;L0:IFL0<0THEN450210IFL0<=ZH1-SORL0>=HZ1+STHENH=0:GOTO440220IFL0>QZ1THENL0=ZH1+(HZ1-L0):REM若欲求横净距断面在曲线后半部,则计算曲线前半部对称位置的横净距230IFL0-SS>=HY1ANDL0+SS<=YH1THENH=R2*(1-COS(S/2/R2)):GOTO440240R=R1:LS=LS1:P=P1:Q=Q1:X0=T1+T1*COS(ZJ):Y0=T1*SIN(ZJ):IFABS(ZJ-PI)<1E-10THENX0=0Y0=2*(R1+P1)250IFL0<=ZH1THENA0=PI/2:X=L0-ZH1:Y=0:GOTO300260IFL0>=HZ1THENA0=ZJ+PI/2:X=HZ1-L0:Y=0:GOSUB620:GOTO300270IFL0>YH1THENL=HZ1-L0:A0=ZJ+PI/2-L^2/2/R1/LS1:GOSUB600:GOSUB620:GOTO300280IFL0>=HY1THENL=L0-HY1+LS1/2:A0=L/R1+PI/2:GOSUB590:X=X+Q:Y=Y+P:GOTO300290L=L0-ZH1:A0=L^2/2/R1/LS1+PI/2:GOSUB600300XM=X-DT:YM=Y-DR310IFA0=PI/2THENA1=1:B1=0:C1=-XMELSEK=TAN(A0):A1=K:B1=-1:C1=YM-K*XM320R=R2:LS=LS2:P=P2:Q=Q2:X0=T2+T2*COS(ZJ):Y0=T2*SIN(ZJ):IFABS(ZJ-PI)<1E-10THENX0=0:Y0=2*(R2+P2)330A=L0-S/2:B=L0+S/2:GOSUB460:H1=H:A=A+.01:B=B+.01:GOSUB460:A=A-.01:B=B-.01340REM分别以10m、1m、0.1m、0.01m的步距使A、B两点向H值增大的方向移动,以减少计算次数350D=100:IFH<H1THENF=-1ELSEF=1360IFH=H1ANDB<=ZH2THENF=1370IFH=H1ANDA>HZ2THENF=-1380FORI=1TO3:D=D/10:D1=D*F390FORJ=1TO100:A=A+D1:B=B+D1:GOSUB460400IFH<=H1THENA=A-D1:B=B-D1:GOTO420410H1=H:NEXTJ420NEXTI430H=H1-DR440U=CSRLIN:LOCATEU-1,48:PRINT〃横净距:〃;USING〃###.##〃;H:GOTO200450END 460REM计算视线AB与法线MN的交点E至M点的距离H值470G=A:GOSUB520:XA=X:YA=Y480G=B:BOSUB520:XB=X:YB=Y490A2=YB-YA:B2=XA-XB:C2=(XB-XA)*YA-(YB-YA)*XA500AB=A1*B2-A2*A2*B2:XE=(B1*C2-B2*C1)/AB:YE=-(A1*C2-A2*C1)/AB510H=SQR((XE-XM)^2+(YE-YM)^2):RETURN520REM计算行车轨迹线已知桩号的任一点的坐标530IFG<=ZH2THENX=G-ZH2:Y=0:RETURN540IFG>=HZ2THENX=HZ2-G:Y=0:GOSUB620:RETURN550IFLS2=0THENL=G-ZH2:GOSUB590:RETURN560IFG>YH2THENL=HZ2-G:GOSUB600:GOSUB620:RETURN570IFG>HY2THENL=G-HY2+LS2/2:GOSUB590:X=X+Q:Y=Y+P:RETURN580L=G-ZH2:GOSUB600:RETURN590X=R*SIN(L/R):Y=R*(1-COS(L/R)):RETURN600C=R*LS:X=L-L^5/40/C^2+L^9/3456/C^4610Y=L^3/6/C-L^7/336/C^3+L^11/42240!/C^5:RETURN620XI=-X*COS(ZJ)-Y*SIN(ZJ):YI=Y*COS(ZJ)-X*SIN(ZJ)630X=XI+X0:Y=Y1+Y0:TETURN640REM用牛顿迭代法计算LS2650LS2=LS1660FORI=1TO10670FX=LS2^2/24/R2-LS2^4/2688/R2^3+LS2^6/506880!/R2^5-LS1^2/24/R1+LS1^4/2688/R1^3-LS1^6/506880!/R1^5680DX=LS2/12/R2-LS2^3/672/R2^3+LS2^5/84480!/R2^5690LS2=LS2-FX/DX:PRINTLS2:NEXTI700RETURN710BT=LS/2/R:LY=R*ZJ-LS:IFLS=0THEN730720L=LS:GOSUB600:Q=X-R*SIN(BT):P=Y-R*(1-COS(BT))730IFZJ=PITHENRETURN740T=(R+P)*TAN(ZJ/2)+Q:RETURN。
