复系数,实系数,有理系数多项式
有理系数多项式

有理系数多项式有理系数多项式(Rational Coefficient Polynomials)是数学中的重要概念之一。
它是指系数为有理数的多项式,即多项式中的各项系数都是有理数。
在代数学中,有理系数多项式的研究与应用广泛,涉及到多个领域,如代数几何、代数拓扑、数论等。
本文将从不同角度探讨有理系数多项式的相关内容。
一、有理系数多项式的定义与性质有理系数多项式是指形如P(x) = a_nx^n + a_{n-1}x^{n-1} + ... + a_1x + a_0的多项式,其中a_i为有理数,x为变量,n为非负整数。
有理系数多项式具有以下性质:1. 多项式的次数:多项式的次数是指最高次项的次数。
例如,P(x) = 2x^3 + 3x^2 - 4x + 1的次数为3。
2. 多项式的系数:多项式中的系数是指各项中变量的系数。
例如,P(x) = 2x^3 + 3x^2 - 4x + 1中的系数为2、3、-4和1。
3. 多项式的加法与乘法:多项式的加法是指将两个多项式相加,乘法是指将两个多项式相乘。
例如,P(x) = 2x^3 + 3x^2 - 4x + 1和Q(x) = x^2 - 2x + 3的和为R(x) = 2x^3 + 4x^2 - 6x + 4,积为S(x) = 2x^5 + 4x^4 - 7x^3 - 14x^2 + 13x - 3。
4. 多项式的因式分解:多项式的因式分解是指将一个多项式表示为多个因式的乘积。
例如,多项式P(x) = x^2 - 4可以分解为P(x) = (x- 2)(x + 2)。
有理系数多项式在数学中有着广泛的应用,以下是其中一些重要的应用领域:1. 代数几何:代数几何是研究代数方程与几何图形之间关系的数学分支。
有理系数多项式在代数几何中发挥着重要作用,如研究曲线、曲面的方程、性质等。
2. 代数拓扑:代数拓扑是研究代数结构与拓扑空间之间关系的数学分支。
有理系数多项式在代数拓扑中被广泛应用,如研究拓扑空间的同调群、同伦群等。
高等代数第1章.

sihuabin@ 南昌大学理学院数学系
本原多项式
定义 设g(x)=bnxn+bn-1xn-1+…+b1x+b0≠0, bi∈Z,i =0,1,…,n。若bn,bn-1,…,b1,b0没 有异于±1的公因子,即bn,bn-1,…,b1,b0是 互素的,则称g(x)为本原多项式。 注记: (1) 本原多项式一定不为零多项式。 (2) 每个不为零的有理系数多项式都可以 表为一个有理数与一个本原多项式的乘 积;这种表示法除了相差一个正负号外是 唯一的。
sihuabin@ 南昌大学理学院数学系
n+ 2 2
§1.9 有理系数多项式
作为因式分解定理的一个特殊情形,对于任意 的f(x)∈Q[x],若∂(f(x))≥1,则f(x)可唯一分解 成不可约的有理系数多项式的积。 但是,如何作出f(x)的分解式却很复杂,没有 一个一般的方法。 已知:在C上只有一次多项式才是不可约多项式。 在R上,不可约多项式只有一次多项式与 某些二次多项式。 但对于在Q上有任意次数的不可约多项式: x n − 2, ∀n ∈ Z + 例如: 如何判断Q上多项式的不可约性呢?
k
k = 1,2, ⋅ ⋅ ⋅, n ( x − ε n −1 )
故 x n − 1 = ( x − 1)( x − ε )( x − ε 2 )
sihuabin@
南昌大学理学院数学系
在实数域范围内
ε =ε 2kπ k k ε + ε = 2cos ,ε k ε k = 1 k = 1,2, , n
sihuabin@ 南昌大学理学院数学系
多项式学生版

w ww .q bx t.cn多项式0.1基本知识和性质多项式是代数学的一个基本概念,是中学代数的重要内容之一,也是各类数学考试以及数学竞赛内容的重要部分.本节我们先介绍一些多项式的基本概念和性质.定义1.设n 是一个非负整数,称形式表达式a n x n +a n −1x n −1+···+a 1x +a 0(1)为一元多项式.其中,a 0,a 1,···,a n 为实数(或复数).在多项式(1)中,a 0称为常数项,a i x i 称为i 次项,a i 称为i 次项系数.一元多项式常用符号f (x ),g (x ),···或者f,g,···等来表示.定义2.如果在多项式f (x )与g (x )中,同次项系数都相等,则称f (x )与g (x )相等.记为f (x )=g (x ).系数全部为0的多项式称为零多项式,记作0.在多项式(1)中,若a n =0,则称a n x n 为多项式(1)的最高次项或首项,称a n 为最高次项系数或首项系数.此时,n 称为多项式(1)的次数,零多项式是唯一不定义次数的多项式.多项式f (x )的次数记作deg(f (x ))或者∂(f (x )).给定一个数c 以及多项式f (x )=a n x n +a n −1x n −1+···+a 1x +a 0,在f (x )的表达式中用c 代替x 所得的数a n c n +a n −1c n −1+···+a 1c +a 0称作当x =c 时f (x )的值,并用f (c )来表示.这样一来f (x )就定义了一个函数,称为多项式函数.两个多项式相等当且仅当它们定义的多项式函数相等.和数的运算一样,多项式的运算满足加法交换律,加法结合律,乘法交换律,乘法结合律以及乘法对加法的分配律.性质1.f (x )g (x )的首项系数等于f (x )和g (x )的首项系数的乘积,并且∂(f (x )±g (x ))≤max(∂(f (x )),∂(g (x ))),∂(f (x )g (x ))=∂(f (x ))+∂(g (x )).性质2.若f (x )g (x )=0,则或者f (x )=0,或者g (x )=0.1w ww .q bx t.cn2性质3.若f (x )g (x )=f (x )h (x ),并且f (x )=0,则g (x )=h (x ).二.例题例1.设多项式f (x ),g (x )和h (x )的系数全部为实数.证明:若f 2(x )=xg 2(x )+xh 2(x ),(2)则f (x )=g (x )=h (x )=0.例2.设n 为自然数,证明:(1+x )(1+x 2)(1+x 4)···(1+x 2n −1)=1+x +x 2+x 3+···+x 2n −1.(3)例3.试求所有实数p ,使得三次方程5x 3−5(p +1)x 2+(71p −1)x +1=66p.(4)的三个根全部为自然数.例4.给定自然数n 以及二次多项式f (x )=ax 2+bx +c,a =0.试证:最多存在一个n 次多项式g (x ),使得f (g (x ))=g (f (x )).例5.设多项式f (x )=a 0+a 1x +a 2x 2+···+a 2n x 2n =(x +2x 2+···+nx n )2.求证:2n Pk =n +1a k =1n (n +1)(5n 2+5n +2).例6.设多项式f (x )满足条件(1)f (0)=0;(2)f (x )=12(f (x +1)+f (x −1)).求f (x )的表达式.例7.设多项式f (x )=ax 2+bx +c 的系数满足:a,b,c >0,a +b +c =1.证明:若正数x 1,x 2,···,x n 满足x 1x 2···x n =1,则f (x 1)f (x 2)···f (x n )≥1.例8.设a,b,c,d 为实数,多项式函数p (x )=ax 3+bx 2+cx +d 满足:对任何|x |<1,有|p (x )|≤1.求证:|a |+|b |+|c |+|d |≤7.例9.(第28届国际数学奥林匹克预选题)给定自然数n ,试求出所有低于n 次的多项式p (x ),使之满足如下条件:n X k =0p (k )(−1)k C kn =0.(5)三.习题习题1.将多项式f (x )=1−x +x 2−x 3+···+x 16−x 17写成g (y )=a 0+a 1y +a 2y 2+···+a 17y 17的形式,其中y =x +1,每个a i 为常数.试确定a 2的值.w ww .q bx t.cn0.2实系数和复系数多项式3习题2.解方程:x 4−x 2+8x −16=0.习题3.求所有满足f (x 2)=f 2(x )的非零多项式f (x ).习题4.试证明:多项式f (x )=1x 9−1x 7+13x 5−82x 3+32x 对所以整数x 都取整数值.习题5.分解因式:S n (x )=1−x +12!x (x −1)−13!x (x −1)(x −2)+···+(−1)nn !x (x −1)···(x −n +1).习题6.已知非常数实数列a 0,a 1,a 2,···,满足a i −1+a i +1=2a i ,i =1,2,3,···.求证:对于任意自然数n ,p n (x )=a 0C 0n (1−x )n +a 1C 1n x (1−x )n −1+a 2C 2n x 2(1−x )n −2+···+a n −1C n −1nx n −1(1−x )+a n C n n x n 是x 的一次多项式.习题7.设多项式f (x )=ax 3+bx 2+cx +d 当x =−1,x =0,x =1,x =2时取值为整数.试证明:对于任意整数n ,f (n )为整数.习题8.求满足f (x 2−2x )=f 2(x −2)的所有非零多项式f (x ).0.2实系数和复系数多项式一.基本知识和性质在以下两节我们针对复数,实数,有理数和整数的特点,分别讨论复系数,实系数,有理系数和整系数多项式的根和因式分解以及其他相关问题.定理1.(代数基本定理)设f (x )为n (n >0)次复系数多项式,则f (x )至少有一个复根.定理2.任何n (n >0)次复系数多项式恰好有n 个复根(重根按重数计算).定理3.任何n (n >0)次复系数多项式都可以分解为n 个1次复系数因式的乘积.由定理2和定理3,设x 1,x 2,···,x k 为n (n >0)次复系数多项式f (x )的所有复根,重数分别为n 1,n 2,···,n k ,则n 1+n 2+···+n k =n 并且f (x )=a (x −x 1)n 1(x −x 2)n 2···(x −x k )n k .若不讨论复系数多项式的根的相重,即将m 重根看做m 个根,则可以得到多项式的根与系数的关系.事实上,记n (n >0)次复系数多项式f (x )=a 0+a 1x +···+a n −1x n −1+a n x n的n 个根为x 1,x 2,···,x n ,则有f (x )=a n (x −x 1)(x −x 2)···(x −x n ).(6)w ww .q bx t.cn4将(6)展开再比较系数可得根与系数的关系:8>>>>>>>><>>>>>>>>:x 1+x 2+···+x n =−a n −1a n ,X 1≤i<j ≤nx i x j =a n −2a n,······,x 1x 2···x n =(−1)na 1a n.其中常用的是第一个和最后一个等式.反之,当上式成立时x 1,x 2,···,x n 为多项式f (x )=a 0+a 1x +···+a n −1x n −1+a n x n的n 个根.推论1.任何n (n >0)次实系数多项式的非实数的复根两两成对出现.推论2.每一个实系数多项式都可以分解成实系数的一次因式和二次因式的乘积.我们指出,n 次单位根在实际解题过程(尤其是分解因式,多项式的整除等)中具有特殊的作用.在前面几节的某些例题和习题中我们实际已经用到了单位根的部分性质.设1,ω,ω2,···,ωn −1为全部n 次单位根,ω=cos 2πn +i sin 2πn ,则有x n −1=(x −1)(x −ω)(x −ω2)···(x −ωn −1),从而有x n −1+x n −2+···+1=(x −ω)(x −ω2)···(x −ωn −1),这个恒等式经常用到.并且由这个恒等式可知ω,ω2,···,ωn −1为多项式p (x )=x n −1+x n −2+···+1的全部n −1个根.二.例题例1.已知关于x 的方程x 4−(3m +2)x 2+m 2=0的四个实根成等差数列,求m .例2.设n 为自然数,f (x )=x 2+x +1,g (x )=(x +1)2n +1+x n +2.试证明:f (x )|g (x ).例3.设a,b,c 为实数,且多项式f (x )=x 3+ax 2+bx +c 的三个实根成等差数列.试指出a,b,c 应满足的充分必要条件.例4.设多项式f (x ),g (x ),h (x )和p (x )满足f (x 5)+xg (x 5)+x 2h (x 5)=(x 4+x 3+x 2+x +1)p (x 5),(7)试证:(x −1)|f (x ).例5.设复系数n 次多项式f (x )=x n +c n −1x n −1+···+c 1x +c 0满足|f (i )|<1(其中i =√−1).求证:存在实数a,b 使得f (a +bi )=0,且(a 2+b 2+1)2<4b 2+1.w ww .q bx t.cn0.2实系数和复系数多项式5例6.设实系数多项式f (x )=1+a 1x +···+a n −1x n −1+x n 的各项系数非负.证明:如果f (x )有n 个不同的实根,则f (2)≥3n .例7.设f (x )=x n +a 1x n −1+···+a n −1x +a n 与g (x )=x n +b 1x n −1+···+b n −1x +b n 为两个复系数多项式,g (x )的根为f (x )的根的平方.证明:若a 1+a 3+a 5+···和a 2+a 4+a 6+···为实数,则b 1+b 2+···+b n 为实数.例8.设n 次多项式f (x )=x n +a n −1x n −1+···+a 1x +a 0的系数全部为实数,且满足条件0<a 0≤a 1≤a 2≤···≤a n −1≤1.证明:若λ为f (x )的复根,且|λ|≥1则λn +1=1.例9.给定多项式序列如下:P 1(x )=x 2−2,P k (x )=P (P k −1(x )),k =2,3,···.求证:对任意自然数n ,方程P n (x )=x 的解为互不相同的实数.例10.设f (x )和g (x )都是不低于1次的多项式.对于复数a ,f (a )=0当且仅当g (a )=0;f (a )=1当且仅当g (a )=1.求证:f (x )=g (x ).三.习题习题1.设n 为自然数,证明:如果(x −1)|f (x n ),那么(x n −1)|f (x n ).习题2.为使实系数多项式f (x )=x 3+ax 2+bx +c 有三个成等比数列的不同实根,a,b,c 应满足什么条件?习题3.试通过考虑单位根确定所有自然数对(m,n ),使得多项式f (x )=1+x n +x 2n +···+x mn 能被g (x )=1+x +x 2+···+x m 整除.习题4.设n 为自然数,求证:多项式f (x )=x n +1−x n −1有一个模为1的复根的充分必要条件是6|n +2.习题5.设多项式f (x ),g (x )满足条件(x 2+x +1)|f (x 3)+xg (x 3),求证:(x −1)|f (x ),(x −1)|g (x ).(8)习题6.给定复系数n 次多项式f (x )=c 0+c 1x +···+c n x n .求证:存在复数z 0满足|z 0|≤1,且|f (z 0)|≥|c 0|+|c n |.习题7.设l,m,n 为自然数,证明:多项式f (x )=x 3l +x 3m +1+x 3n +2能被g (x )=x 2+x +1整除.习题8.设l,m,n 为自然数,试确定多项式f (x )=x 3l −x 3m +1+x 3n +2能被g (x )=x 2−x +1整除的条件.习题9.设l,m,n 为自然数,试确定多项式f (x )=x 3l +x 3m +1+x 3n +2能被g (x )=x 4+x 2+1整除的条件.。
复系数和实系数多项式

定理 实系数不可约多项式或为一次或为形如ax2 bx c
的二次多项式, 其中b2 4ac 0.
所以 上一元多项式的标准分解式为
m
r
f ( x) d ( x ai )li ( x2 bj x c j )hj
其中ai
i 1
且两两互异,
li
j1
是正整数(i
1,2,, m);
bj ,cj
的多项式.
解
因0
f
(ci )
ancin
an1cin1
ac 1i
a 且c
0
i
0,
所以
0
cn i
f
(ci
)
an
a c1 n1 i
a c( n1) 1i
a cn 0i
,
令 g(x)
a0 xn
a xn1 1
an1 x an ,
则
g(
1 ci
)
0.
又 c1,c2 ,,cn 非零且两两互异,所以 g(x)为所求.
,
hj
是正整数,
b
2 j
4c
j
0
且x2 bjx cj
两
两互素( j 1,2,,r)
l m
i1 i
2
h r
j1 j
deg
f
( x).
5.6 复系数和实系数多项式
例1
设f
(
x
)
an
x
n
an1
x
n1
a 1
x
a 0
的n个互
异的非零根为 c1,c2 ,,cn ,
求以
1 c1
,
1 c2
实系数多项式
55
第一章 多项式
若 不为实数,则 也是 f ( x) 的复根,于是
f ( x) ( x )( x ) f2( x) x2 ( )x f2( x)
设 a bi ,则 a bi, 2a R , a2 b2 R 即在R上 x2 ( )x 是 一个二次不可约多项式.
从而 ( f2 ) n 2. 由归纳假设 f1( x) 、f2( x)可分解成一次因式与二次
不可约多项式的乘积. 由归纳原理,定理得证.
§8 复系数与实系数多项式的因式分解 © 2009, Henan Polytechnic University
66
推论1
第一章 多项式
f ( x) R[ x], f ( x) 在R上具有标准分解式 f ( x) an( x c1)k1 ( x c2 )k2 ( x cs )ks ( x2 p1x q1)l1
一、复系数多项式
第一章 多项式
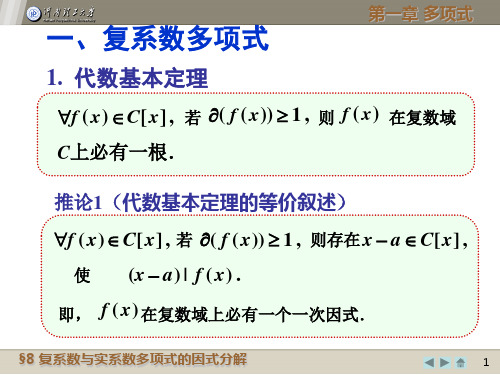
1. 代数基本定理
f ( x) C[x] , 若 ( f ( x)) 1 , 则 f ( x) 在复数域 C上必有一根.
推论1(代数基本定理的等价叙述) f ( x) C[x] , 若 ( f ( x)) 1 , 则存在 x a C[x] ,
f ( x) a( x 1)r1 ( x 2 )r2 ( x s )rs
其中1,2 , ,s是不同的复数,r1,r2, ,rs Z+
推论2 f ( x) C[x],若 ( f ( x)) n ,则 f ( x) 有n个 复根(重根按重数计算).
§8 复系数与实系数多项式的因式分解 © 2009, Henan Polytechnic Un多项式
高等代数实系数和复系数多项式的因式分解

−
n−2
(ε 2
+
ε
n+2 2
)x
+
1].
. . . .... .... .... . . . . .... .... .... . .
. .. . . ..
例题选讲
例 设 f(x), g(x) 是两多项式,且 f(x3) + xg(x3) 可被 x2 + x + 1 整除, 则 f(1) = g(1) = 0.
两边取共轭数,有
f(α¯) = anα¯n + an−1α¯n−1 + · · · + a0 = 0,
这就是说,f(α¯) = 0,α¯ 也是 f(x) 的根.
. . . .... .... .... . . . . .... .... .... . .
. .. . . ..
实系数多项式因式分解定理
. .. . . ..
高斯与代数基本定理
代数基本定理在代数乃至整个数学中起着基础作用. 据说,关于 代数学基本定理的证明,现有 200 多种证法. 迄今为止,该定理 尚无纯代数方法的证明. 大数学家 J.P. 塞尔曾经指出:代数基本 定理的所有证明本质上都是拓扑的. 美国数学家 John Willard Milnor 在数学名著《从微分观点看拓扑》一书中给了一个几何直 观的证明,但是其中用到了和临界点测度有关的 sard 定理. 复变 函数论中,对代数基本定理的证明是相当优美的,其中用到了很 多经典的复变函数的理论结果.
. . . .... .... .... . . . . .... .... .... . .
. .. . . ..
高斯与代数基本定理
该定理的第一个证明是法国数学家达朗贝尔给出的,但证明不完 整. 接着,欧拉也给出了一个证明,但也有缺陷,拉格朗日于 1772 年又重新证明了该定理,后经高斯分析,证明仍然很不严 格的. 代数基本定理的第一个严格证明通常认为是高斯给出的 (1799 年在哥廷根大学的博士论文),高斯后来又给出了另外三个 证法,其中第四个证法是他 71 岁公布的,并且在这个证明中他 允许多项式的系数是复数.
高等代数 第三版§1.8 复、实系数多项式

k1 , , ks , l1 , , l s Z ,
p2 4q 0, i 1,2 r ,即 x 2 pi x qi 为 且
R上的不可约多项式.
推论2 实数域上不可约多项式只有一次多项式和某些二 次不可约多项式,所有次数≥3的多项式皆可约. 例1 求 x n 1 在 C 上与在 R 上的标准分解式. 在复数范围内 x n 1 有n个复根,
解: 1)
1, , , ,
2
n1
这里
k
2 2 cos i sin , n 1 n n k 1,2, , n
2 n1
2k 2k cos i sin , n n
∴ 2)
x 1 ( x 1)( x )( x )( x
Higher Algebra
一、复系数多项式
二、实系数多项式
一、复系数多项式
1. 代数基本定理
f ( x ) C [ x ] , 若 ( f ( x )) 1 , 则 f ( x ) 在复数域 C上必有一根.
推论1
f ( x ) C [ x ] , 若 ( f ( x )) 1 , 则存在 x a C [ x ] ,
若 为根,则 f ( ) an n an1 n1 a0 0
两边取共轭有
f ( ) an an1
n
n1
a0 0
∴ 也是为 f ( x ) 复根.
实系数多项式因式分解定理
f ( x ) R[ x ],若 ( f ( x )) 1, 则 f ( x ) 可唯一
使
(x a ) | f ( x ) .
7多项式

7多项式多项式是竞赛数学的重要内容之一。
因为多项式可看成特殊的函数,因而可用函数的方法解决一些多项式问题。
多项式的根是方程的根,因而多项式与方程及复数有密切的关系。
对于整系数多项式,当自变量取整数时,多项式的值也为整数,从而多项式可与数论实行综合。
多项式理论本身有很多重要结论,由此出发我们能研究多项式的性质。
正因为多项式与众多学科密切相关,因而在竞赛数学中受到高度的重视。
1.基本原理多项式的结论常与多项式的系数所在的集合相关,为了叙述方便,我们约定:用[][][][]x C x R x Q x Z ,,,分别表示整系数、有理系数、实系数、复系数的所有一元多项式的集合,用()x f deg 表示多项式()x f 的次数。
在高等代数中,我们得到了多项式的很多重要结论,为了便于应用,现将部分结论列举如下:定理1(带余除法)设()()x g x f ,是多项式,()0≠x g ,则存有唯一多项式()x q 与()x r ,使得()()()()x r x g x q x f += , 这里()0=x r 或()()x g x r deg deg <。
定理2(整系数环上的带余除法)设()()x g x f ,是整系数多项式,()0≠x g 且()x g 的首项系数为1,则存有唯一的整系数多项式()x g 和()x r ,使得()()()()x r x g x q x f += , 这里()0=x r 或()()x g x r deg deg <。
定理3(余数定理)多项式()x f 除以()a x -所得的余数为()a f 。
推论1(因式定理)多项式()x f 有因式()a x -的充要条件是a 为()x f 的根。
推论2 ()()a f x f a x --| 。
推论3 若[]x Z x f ∈)(,则()()b f a f b a --|。
定理4 一元)0(>n n 次多项式恰有n 个根,重根按重数计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
任意一个有理系数多项式总可转化 为整系数多项式.
介绍一类重要的整系数多项式: 介绍一类重要的
1、本原多项式
设 f (x) = anxn + an-1xn-1 + … + a0 是一有理系数多项式. 选取适当的整数 c 乘 f (x) , 总可以使 c f (x) 是一整系数多项式. 如果 c f (x) 的 各项系数有公因子,就可以提出来,得到 c f (x) = d g(x) , 也即
f (α ) = anα n + an-1α n-1 + … + α0 = 0 .
定理 4.6 (实系数多项式因式分解定理)每个次数≥1 的实系数多项式 f (x) 在实数域上都可以唯一地分解 成一次因式与二次不可约因式的乘积.
证明 定理对一次多项式显然成立.
假设定理对次数 < n 的多项式结论成立. 则当 f (x) 是 n 次实系数多项式时, 由代数基本定理, f (x) 在复数域内一定有一根 α . 如果 α 是实数,那么 数域内 f (x) = (x - α ) f1(x) , 其中 f1(x) 是 n - 1 次实系数多项式.
多项式. 由归纳法假设, f1(x) 或 f2(x) 可以分解成 一次与二次不可约多项式的乘积,因此,实系数多 项式在实数域上都可以唯一地分解成一次因式与二 次不可约因式的乘积.
证毕
实系数多项式的标准分解式
f ( x) = an ( x − c1 )
l1
( x − cs ) ( x + p1 x + q1 )
2 例如, 方程 x − 2 = 0 在有理数域上没有根, 但在实数域 上有根: x = ± 2.
2 又如,方程 x + 1 在实数域上没有根,但是,在复数域上 有根:
x = ± i.
定理 4.2 F[x] 中 n 次多项式 ( n ≥ 0 ) f (x)在数
域 F中的根不可能多于 n 个,重根按重数计算.
重因式(k ≥ 1),那么 p(x) 是 f (x) , f ′(x) , … , f (k-1)(x) 的因式,但不是 f (k)(x) 的因式.
一元代数方程
f ( x ) = a n x n + a n −1 x n −1 + ⋅ ⋅ ⋅ + a1 x + a0 = 0
的基本问题是:它有无根?有多少根?如何求出它 的全部根? 当n较大时,这是一个复杂问题,且与x的范围有关.
推论 如果数域 F上的 n次多项式f(x)在F上有 n+1 个不同的根,则它恒等于零。
证明 由已知条件,有 f (αi ) = 0 , i = 1 , 2 , … , n + 1 , 即,f(x)与零多项式对 n + 1 个不同的数 α1 , α2 , … , αn+1 有相同的值, 由定理 4.3, f (x) = 0 . 证毕
式在复数域中有一根. 利用根与一次因式的关系(定理 4.1 及其推论) 代数基本定理可以等价地叙述为: 每个次数 ≥ 1 的复系数多项式,在复数域上一 定有一个一次因式.
注释
在复数域上所有次数大于 1 的多项式
全是可约的. 即,不可约多项式只有一次多项式. 于是,因式分解定理在复数域上可以叙述成:
定理 4.5 (复系数多项式因式分解定理)
证明
零次多项式有零个根, 对零次多项式定理成立.
设 degf (x)=n > 0 , 把 f (x) 分解成不可约多项式的 乘积:
f ( x) = a ( x − r1 )
α1
( x − rl )
αl
plα+l+1 ( x) 1
pαs ( x), s
其中, pi ( x) > 1,(i = l + 1, , s) deg
如果 α 不是实数, 那么 α 也是 f (x) 的根且 α ≠ α . 于是 f (x) = (x - α ) (x - α ) f2(x) .
显然 (x - α ) (x - α ) = x2 - ( α + α )x + αα 是一实系 数二次不可约多项式. 从而 f2(x) 是 n - 2 次实系数
d f ( x ) = g( x ) , c
其中 g(x) 是整系数多项式,且各项系数没有异于 ±1 的公因子. 例如
2 4 2 4 2 2 x − 2x − x = (5x −15x2 − 3x). 3 5 15
定义4.1 如果一个非零的整系数多项式
g (x) = bnxn + bn-1xn-1 + … + b0 的系数 (bn , bn-1 , … , b0 )=1,也就是说,它们 是互素的,它就称为一个本原多项式. 引理2 任何一个非零的有理系数多项式 f (x) 都可以 表示成一个有理数 r 与一个本原多项式 g (x) 的乘积: f (x) = r g(x) . 且这种表示法除了差一个正负号外是唯一的.
第四节
复系数、实系数、 有理系数多项式
一、多项式函数
在这一节, 我们将从函数的观点来考察多项式. 设 f (x) = anxn + an-1xn-1 + … + a1x + a0 (1) 是 F[x] 中的多项式,α 是 F 中的数,在 (1) 中用 α 代 x 所得的数 anα n + an-1α n-1 + … + a1α + a0 称为 f (x) 当 x = α 时的值,记为 f (α ) . 时的值 此时,多项式 f (x) 就定义了一个数域 F上的函数. 我们称为数域F 上的多项式函数. 当F是实数域时,就是数学分析中讨论的多项式函数.
那么就有一个素数 p 能整除 h (x) 的每一个系数. 因为 f (x) 是本原的,所以 p不能同时整除 f (x) 的每一个系数. 令 ai 是第一个不能被 p 整除的系数,即
p | a0 , … , p | ai-1 , p | ai .
同样地, g (x) 也是本原的, 令 bj是第一个不能被 p 整除的系数, 即
项式恰有 n 个复根(重根按重数计算) .
三、实系数多项式
引理1 如果 α 是实系数多项式 f (x) 的复根,那么
α 的共轭数 α 也是 f (x) 的根. P20,习题1.4.6
证明 设 f (x) = anxn + an-1xn-1 + … + a0 , 由假设 其中 a0 , a1 , … , an 是实数. 两边取共轭数,有 f (α ) = anα n + an-1α n-1 + … + a0 = 0 , 这就是说, f (α ) = 0, α 也是 f (x) 的根. 证毕
由定理 4.1的推论与根的重数定义,f (x) 在数域 F 中 4.1 中根的个数等于分解式中一次因式的个数, 这个数目为 α1 + α 2 +
+ α l ≤ n.
证毕
问题
不同的多项式会不会定义出相同 的函数呢?
即,是否可能有 f (x) ≠ g(x) , 而对于 F 中所有的数 α 都有 f (α ) = g(α ) ? 由定理 4.2 不难对这个问题给出一个否定的回答.
( x -α ) | f (x) . 由这个关系,我们可以定义重根的概念. α 称 为 f (x) 的 k 重根,如果 ( x -α ) 是 f (x) 的 k 重因式. 重根 重因式 当 k = 1 时,α 称为单根;当 k > 1 时,α 称为重
根.
推论 1 如果不可约多项式 p(x) 是 f (x) 的 k
p | b0 , … , p | bj-1 , p | bj .
考察 h (x) 的系数 di+j , 由乘积的定义 di+j = aibj + ai+1bj-1 + ...+ai+j b0 + ai-1bj+1 + ai-2bj+2 + … +a0bi+j 由假设,p 整除di+j ,p 整除右 端aibj 以外的每一项, 但是 p 不能整除 aibj . 矛盾!因此, h (x) 是本原多项式. 证毕
二、复系数多项式
以上我们讨论了在一般数域上多项式, 下面 考察在复数域与实数域上多项式. 复数域与实数域既然都是数域,因此前面所 得的结论对它们也是成立的. 但是这两个数域又有 它们的特殊性,所以某些结论就可以进一步具体化. 对于复数域,我们有下面重要的定理:
定理 4.4(代数基本定理) 每个次数 ≥ 1 的复系数多项
f (x) = ( x -α ) q(x) + f (α )
如果 f (x) 在 x = α 的函数值 f (α ) = 0,那么α 就称为 f (x) 的一个根或零点. 由余数定理: 零点 f (x) = ( x -α ) q(x) + f (α ) , 得到根与一次因式的关系:
推论 α 是 f (x) 的根的充分必要条件是
ls 2
k1
( x2 + pr x + qr )kr ,
其中 c1 , … , cs , p1 , … , pr , q1 , … , qr 全是实数, l1 , … , ls , k1 , … , kr 是正整数,并且 x2 + p i x + qi ( i = 1 , 2 , … , r ) 在实数域上是不可约的,即, 适合条件 在实数域上 pi2 - 4 qi < 0, i = 1 , 2 , … , r .
每个次数 ≥ 1 的复系数多项式在复数域上都可 以唯一地分解成一次因式的乘积. 因此,复系数多项式具有标准分解式
f ( x ) = an ( x − α 1 ) ( x − α 2 )
