相干叠加与非相干叠加叠加条件
第三章 干涉

两波到达P点的相位差为:
2 1 2 ( n2 r2 n1r1 ) ( 01 02 ) 2 c c ( 2 c , n1 , n2 ) 1 2
( r2 r1 ) ( 01 02 )
1、相位差
2
频率相等,振动方向(光矢量 E )平行、相
位差恒定。
3、波动的特征 “干涉”和“衍射”现象是波动的重要特征。
四、相干叠加与非相干叠加
1、两简谐振动的合成
1 A t 1 ) 1 cos(
2 A2 cos( t 2 )
1 2 A cos( t )
'
dx r2 r1 d sin d tan D
考虑到移动方向相反
D x s R
例1:用白光做光源观察双缝干涉,缝间距为d,试 求能观察到的清晰可见光谱的级次。白光波长范围 390—750nm。
例2:一双缝实验中,两缝间距为0.15mm,在1.0m处 测得第一级和第十级暗纹之间距离为36mm。试求所 用单色光的波长。
——分波阵面法
(3) 劳埃德镜
P'
P
s1
d
s2
M
L
d'
半波损失 :光由光疏介质射向光密介质时, 反射光相位突变π 。
三、干涉条纹的移动
零级条纹在P0 光源移动δs 条纹移动δx
R2 r2 R1 r 1
R1 R2 (r1 r2 )
傍轴, 小角度下:
R1 R2 d sin ' ds d tan R
n2 n
2
Q
2 L 2h n 2 n1 sin 2 i1
光的相干叠加

光程差每改变1个波长,条纹移动1个间隔
干涉条纹的反衬度(可见度)
• 反衬度的定义:在接收屏上一选定的区域 中,取光强最大值和最小值,有
IM Im
IM Im
I M ( A1 A2 ) 2 , I m ( A1 A2 ) 2
2 A1
2 A1 A2
A2
A12 A22 1 ( A1 )2
R1 S1
•
O
R2
S2
S1
h
S2 b
• R1 S1
R2
S2
向
O
上 移
动
?
O
0
L (R2 r2 ) (R1 r1) 0
条纹位移x与 点源位移s的 关系
单色点光源 s •
R1 s1 d
R2 s2 R
r1
r2
D
x
·
x
0
z
定点考察0
L (R2 r2 ) (R1 r1) 0
R s; D d
或条纹的
fx
1 x
空间频率 (空间周期 性的直观)
fy
1 y
x Y y
4.3 惠更斯—菲涅耳原理
• 一.光的衍射现象 • 波绕过障碍物继续传播,也称绕射 。 • 二.次波 • 光波是振动的传播,波在空间各处都引起
振动。 • 波场中任一点,即波前上的任一点,都可
视为新的振动中心。 • 这些振动中心发出的光波,称为次波。
A1
cos
(2
n1r1
t 01)
2 A2 cos(k2r2 t 02 )
A2
cos(2
n2r2
t
02 )
P(x, y, z) r1
S1
大学物理_光的干涉

一.光的机械微粒学说(17世纪--18世纪末)
代表:牛顿 v水 v空气 对立面:惠更斯--波动说 v水 v空气
分歧的焦点:光在水中的速度
1850年佛科(Foucauld)测定 v水 v空气
微粒说开始瓦解
二.光的机械波动说(19世纪初--后半世纪)
二.光的机械波动说(19世纪初--后半世纪)
等倾干涉
§14-4 分割振幅法产生的光的干涉
一. 薄膜干涉(最典型)
2e
n22
n12
sin2
i
2
二. 等厚干涉
=
k (2k 1)
2
(明) (暗)
1.劈尖干涉
1.劈尖干涉
sin i 0
n1
设每一干涉条纹对应的薄膜厚度分别为:
e1 .e2 .e3 ek
{
ek1 ek 2n2
l=
2n2 sin
条纹为平行于棱边明暗 相间等间隔的直条纹, 棱边处(e=0)为暗纹
2.增透与增反
问题:组合透镜中,反射光能损失20%左右 解决办法:在透镜表面镀膜
增反:
2n2e k k 0,1
增透(减反):
2n2e (2k 1) 2 k 0,1
D
x明 k 2a
4).整个双缝实验装置放入水中
复习: 14-1,2,3
预习: 14-4
作业: 练习十二
例3:在杨氏双缝实验中,
x
当作如下调节时,观察屏
S1
上的干涉条纹将如何变化 2a
r1
r2
P O
并说明理由
S2
D
光的干涉 知识点总结材料

第二章 光的干涉 知识点总结2.1.1光的干涉现象两束(或多束)光在相遇的区域产生相干叠加,各点的光强不同于各光波单独作用所产生的光强之和,形成稳定的明暗交替或彩色条纹的现象,称为光的干涉现象。
2.1.2干涉原理注:波的叠加原理和独立性原理成立于线性介质中,本书主要讨论的就是线性介质中的情况. (1)光波的独立传播原理当两列波或多列波在同一波场中传播时,每一列波的传播方式都不因其他波的存在而受到影响,每列波仍然保持原有的特性(频率、波长、振动方向、传播方向等) (2)光波的叠加原理在两列或多列波的交叠区域,波场中某点的振动等于各个波单独存在时在该点所产生振动之和。
波叠加例子用到的数学技巧: (1) A +iB =√A 2+B 2(A √A 2+B2+i B √A 2+B 2)=A t e iφt(2)eiφ1=ei[(φ12+φ22)+(φ12−φ22)] eiφ1=ei[(φ12+φ22)−(φ12−φ22)]注:叠加结果为光波复振幅的矢量和,而非强度和。
分为相干叠加(叠加场的光强不等于参与叠加的波的强度和)和非相干叠加(叠加场的光强等于参与叠加的波的强度和). 2.1.3波叠加的相干条件干涉项:相干条件:(干涉项不为零) (为了获得稳定的叠加分布) (为了使干涉场强不随时间变化) 2.1.4 干涉场的衬比度1.两束平行光的干涉场(学会推导) (1)两束平行光的干涉场 干涉场强分布:21ωω=10200⋅≠r rE E 2010ϕϕ-=常数()()212121212()()()2=+⋅+=++⋅r r r r r r r r rI r E E E E I r I r E E 12102012201021212010212{cos()()()cos()()()}⋅=⋅+⋅++-++-⋅+---r r r r v v v v vE E E E k k r t k k r t ϕϕωωϕϕωω()()()*12121212,(,)(,)(,)(,)2cos =++=++∆%%%%I x y U x y U x y U x y U x y I I I I ϕ亮度最大值处:∆φ=2mπ亮度最小值处:∆φ=(2m +1)π 条纹间距公式∆x =λsin θ1+sin θ2空间频率:ƒ=1∆x ⁄(2)定义衬比度以参与相干叠加的两个光场参数表示:衬比度的物理意义 1.光强起伏2.相干度2.2分波前干涉2.2.1普通光源实现相干叠加的方法 (1)普通光源特性• 发光断续性 • 相位无序性• 各点源发光的独立性根源:微观上持续发光时间τ0有限。
光波的相干叠加.

令 n
n 0,1,2,
2
1
nD 明纹: xn ( D sin ) d
相邻两明纹间的距离为:
D x xn 1 xn d
结论:斜入射时,各级条纹沿某方向平移,但相邻条纹 间距不变。
10
思考:(1)中央明纹位于何处? (2)斜向上入射时,结果如何?
8
(2)以白光入射时:
Δx与λ成正比,用白光做光源时,除中央明纹是白光 外,其它各级条纹是彩色条纹,紫在内红在外;不重 叠的称为完整的光谱。(k+1)Dλ 1/d≤kDλ2/d λ 1与 λ2为整数比时,某些级次 的条纹发生重叠。 k1 λ 1=k2 λ2
x
k 1
k
讨论题: 1. 如果用两个灯泡分别照亮S1、S2缝,能否看到干涉条纹?
O
代入(1)式,可得明纹中心的位置:
D x =± n d
n = 0,1,2,
n=0, 中央明纹;任一n值,第n级明纹。 n: 条纹的级数。
6
x1
D
d
; x 2
2D d
……
相邻两明纹间的距离为:
x 将 sin tg D
D x d
代入(2)式,可得暗纹中心的位置:
r1
P
r2
(3)光源不动,上下平移双缝时,结 果如何?
d
2
x
1
O
D
例题:用λ1=450nm和λ2=600nm的两种光正入射于双缝, 若D、d已知,求屏上这两种光第二次重叠的位置。(不含中 央明纹) 解:设重叠处λ1为第n1级,λ2为第n2级,则有:
n11 D n22 D x d d
《物理光学》简答题
《物理光学》简答题第4章光的电磁理论1由“玻⽚堆”产⽣线偏振光的原理是什么?答:采⽤“玻⽚堆”可以从⾃然光获得偏振光。
其⼯作原理是:“玻⽚堆”是由⼀组平⾏平⾯玻璃⽚叠在⼀起构成的,当⾃然光以布儒斯特⾓(B)⼊射并通过“玻⽚堆”时,因透过“玻⽚堆”的折射光连续不断地以布儒斯特⾓⼊射和折射,每通过⼀次界⾯,都会从⼊射光中反射掉⼀部分振动⽅向垂直于⼊射⾯的分量,当界⾯⾜够多时,最后使通过“玻⽚堆”的透射光接近为⼀个振动⽅向平⾏于⼊射⾯的线偏振光。
2解释“半波损失”和“附加光程差”。
答:半波损失是光在界⾯反射时,在⼊射点处反射光相对于⼊射光的相位突变,对应的光程为半个波长。
附加光程差是光在两界⾯分别反射时,由于两界⾯的物理性质不同(⼀界⾯为光密到光疏,⽽另⼀界⾯为光疏到光密;或相相反的情形)使两光的反射系数反号,在两反射光中引⼊的附加相位突变,对应的附加光程差也为半个波长。
第5章光的⼲涉1相⼲叠加与⾮相⼲叠加的区别和联系?区别:⾮相⼲叠加(叠加区域内各点的总光强是各光波光强的直接相加);相⼲叠加(叠加区域内各点的总光强不是各光波光强的直接相加,有强弱分布)。
联系:相⼲叠加与⾮相⼲叠加都满⾜波叠加原理。
2利⽤普通光源获得相⼲光束的⽅法答:可分为两⼤类:分波阵⾯法由同⼀波⾯分出两部分或多部分⼦波,然后再使这些⼦波叠加产⽣⼲涉。
(杨⽒双缝⼲涉是⼀种典型的分波阵⾯⼲涉。
)分振幅法:1)利⽤薄膜的上、下表⾯反射和透射,将⼀束光的振幅分成两部分或多部分,再将这些波束相遇叠加产⽣⼲涉。
(薄膜⼲涉、迈克⽿逊⼲涉仪和多光束⼲涉仪都利⽤了分振幅⼲涉。
)2)利⽤晶体的双折射将⼀束线偏振光分为两束正交的偏振光,经过不同的相移后叠加(在同⼀⽅向的分量叠加)产⽣⼲涉(分振动⾯⼲涉)。
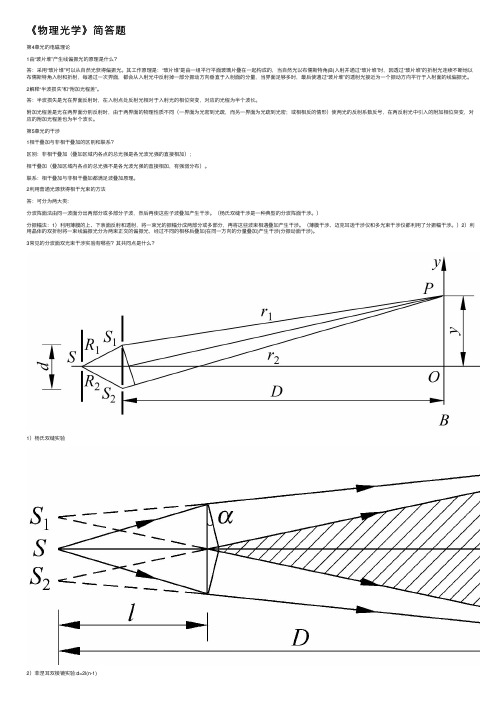
3常见的分波⾯双光束⼲涉实验有哪些?其共同点是什么?1)杨⽒双缝实验2)菲涅⽿双棱镜实验:d=2l(n-1)3)菲涅⽿双⾯镜实验:d=2l4)洛挨镜实验:d=2a(有半波损失)共同点:1)在整个光波叠加区内都有⼲涉条纹,这种⼲涉称为⾮定域⼲涉;2)在这些⼲涉装臵中,为得到清晰的⼲涉条纹,都要限制光束的狭缝或⼩孔,因⽽⼲涉条纹的强度很弱,以致于在实际上难以应⽤。
第1节 光波的相干叠加(1)

第 1 节光波的相干叠加一、光源 1、原子发光图像 物体发光的原因是原子中电子的跃迁,处于激发态的电子不稳定,它会向低能级跃迁,能量以电磁波的形式发散出来,这就是原子发光。
即使是同一个原子,不同时刻发出的电磁波,其相位和振动方向一般不同。
所以同一光源不同点发出的光线,一般不是相干光。
两个普通光源发出的光,一般也不是相干光。
2、光的相干条件以及双光束干涉的强度分布 几列波在空间相遇时,只要各自的扰动不十分强烈,且所处介质具有线性响应特性,则各波可以保持其原有的传播特性,即频率、振幅、振动方向等不变,并在离开相应区域后 仍按各自原来的行进方向独立地前进,彼此无影响。
当几列波在同一空间传播时,相遇的区域内各点将同时参与每列波在该点的扰动。
合扰动等于各列波单独在该点产生的扰动的线性叠加。
说明:(1)对于机械波而言,即介质质点的振动;对光波而言,即电场强度矢量的变化。
(2)所谓线性叠加,对于标量波而言,叠加波的波函数等于参与叠加的各列波的 波 函数的代数和;对于矢量波而言,叠加波的波函数等于各列波波函数的矢量和。
(3)线性叠加性质以独立传播性质为前提条件,是波动方程具有线性性质的必然 结 果。
波动方程是否满足线性条件取决于波的扰动强度和所处介质的响应特性。
波的扰动强度 较小或该介质对扰动有线性响应,即线性叠加性质及独立传播性质均成立;波的扰动强度较 大或介质对扰动有非线性响应,两都将不再成立。
定义光强为:。
两列波在空间中的 P 点相遇,可求得合振动矢量与强度:(1)当两列波的振动方向垂直时,,此时:(2)当两列波的振动方向平等时,,此时:(3)干涉的意义: 假设:某时刻两列同频率且振动方向平行的矢量波,在空间相遇点 P 的振动状态:1其中:这说明,瞬时叠加强度不仅与两列波各自的强度大小有关,而且还与两列波在叠加 点的相位差有关。
相位差不同,叠加强度的大小不同。
因此,相遇区的瞬时叠加强度将呈现 出一种非均匀分布。
现代光学工程-3 光的干涉

稳定干涉的三个条件: 稳定干涉的三个条件:
v 2 v 2 v v I ( P) = U1 + U 2 + 2 U1 ⋅ U 2
两列波的扰动方向一致,或有方向一致的平行分量。如果正交, (1)两列波的扰动方向一致,或有方向一致的平行分量。如果正交,必然 v v 2 v 2 v 2 v v 是非相干叠加。 是非相干叠加。 I ( P ) = U1 + U 2 = U1 + U 2 + 2 U1 ⋅ U 2 (2)频率相同是相干的另一条件。两列波若频率不同,必然为非相干叠加。 )频率相同是相干的另一条件。两列波若频率不同,必然为非相干叠加。
由普通光源获得相干光的途径(方法)有两类: 由普通光源获得相干光的途径(方法)有两类:
分波前干涉
从同一波面上的不同部分产生次级波相干
分波面法,如:杨氏双孔干涉 分波面法 如
p
S*
分振幅干涉
利用光的反射和折射将同一光束分割成振幅 较小的两束相干光 ·p S * 分振幅法, 分振幅法,如:薄膜干涉 薄膜
ω1 ≠ ω2,此时I (P ) = I1 (P ) + I 2 (P ),为非相干叠加。 ω1 = ω2,∆I (P ) = A1 A2 cos(ϕ1 − ϕ 2 ) = 2 I1 I 2 cos δ ( P)
(3)稳定的相位差,才能获得稳定干涉图样。 )稳定的相位差,才能获得稳定干涉图样。
I ( P) = I1 ( P) + I 2 ( P) + 2 I1 I 2 cos δ ( P )
r2 − r1 = 常数
的点的轨迹是
对称装置,R1=R2
相同的点,干涉情况相同。数学证明 以两点光源为焦点的回旋双曲面。
光的干涉

洛埃镜
S1 d S2 M
E'
E
洛埃镜
此处为暗纹—半波损失
M为反射镜,S1为狭缝光源,它发出的光波一部分以接近于 为反射镜, 为狭缝光源, 为反射镜 90˚的入射角掠射于反射镜上,经反射到达屏幕 上,另一部 的入射角掠射于反射镜上, 的入射角掠射于反射镜上 经反射到达屏幕E上 分直接射到屏幕上。 可看作两个相干光源。 分直接射到屏幕上。S1和S2可看作两个相干光源。 处于位置 若光屏E处于位置 ,从光路上看,由S1和S2发出的光到达接 光屏 处于位置E',从光路上看, 触处的路程相等,该处应该出现明条纹。 触处的路程相等,该处应该出现明条纹。但实验结果这里出现 的是暗条纹,说明反射光在该处出现了大小为π的相位变化 的相位变化, 的是暗条纹,说明反射光在该处出现了大小为 的相位变化, 这种现象称为“半波损失” 这种现象称为“半波损失”。
例题 4-4:
干涉现象应用于射电天文学: 干涉现象应用于射电天文学:将微波检测器安装在海平面上 h = 20m处。 处 当发射频率为ν= 60 MHz 的射电星从海面升起时,检测器收到来自星体和 当发射频率为 的射电星从海面升起时, 海面反射的电波干涉信号。求当第一个极大出现时, 海面反射的电波干涉信号。求当第一个极大出现时,射电星体相对于地平 线的仰角θ= 线的仰角 ?
获得相干光的基本方法是将光源上同一点发出的光设法 获得相干光的基本方法是将光源上同一点发出的光设法 同一点 一分为二” 然后再使这两部分光叠加起来, “一分为二”,然后再使这两部分光叠加起来,由于这两 部分光实际上都是来自同一发光原子 同一次发光, 同一发光原子的 部分光实际上都是来自同一发光原子的同一次发光,即每 一个光波列都分为两个频率相同、振动方向相同、 一个光波列都分为两个频率相同、振动方向相同、相位差 恒定的波列,因而这两部分光满足相干条件。 恒定的波列,因而这两部分光满足相干条件。 获得相干光的方法: 获得相干光的方法: ⑴使用单色光源(如:钠光灯、激光器等); 使用单色光源( 钠光灯、激光器等); ⑵将一个分子单次发出的光波分为两个部分: 将一个分子单次发出的光波分为两个部分: 分波面法 分振幅(强度) 分振幅(强度)法
5.2 相干叠加与非相干叠加 叠加条件

I max ( A1 A2 )
2
合振动平均强度达到最大值,称为干涉相长。
物理科学与信息工程学院 10
如果两振动相位差
2 1 (2 j 1) ( j 0,1,2,3.....)
则合振动的强度为
I min ( A1 A2 )
2
合振动平均强度达到最小值,称为干涉相消。 如果相位差为其他值,则合振动的强度介于Imax和 Imin之间。
2. 相干叠加 如果在观察时间内,两电磁振动各自连续进行, 并不中断(这种观察在光学中很少遇见) 。
它们初相位差,也就是说任意时刻的相位差, 2 1 始终保持不变,与时间无关。则上式末项的积分值为 : Nhomakorabea
1
0
cos( 2 1 )dt cos(2
2 2 A1
1 )
则合振动的平均强度为:
物理科学与信息工程学院 5
在某一时间间隔内 (其值远大于光振动的 周期
T,例如可见光波段,T约为10-15s),则合振动 的平均相对强度为:
IA
2
2 2
1
0
A dt
2
A
1
0
2 1
2 1
2 A2 2 A1 A2 cos( 2 1 ) dt
A A 2 A1 A2
物理科学与信息工程学院 7
即 则
2 1 f (t )
1 cos( 2 1 )dt 0
0
因此合振动的平均光强为
I A A A
2 2 1
2 2
合振动的平均强度等于分振动强度之和。 其干涉项的平均值为0,两振动叠加后没有强度减 弱的情况,此即非相干叠加。
第一章光干涉

光程差为两束光的光程之差。
L2 L1 n2r2 n1r1
例 在相同的时间内,一束波长为的单色光在空气中
和在玻璃中
(A)传播的路程相等,走过的光程相等。
(B)传播的路程相等,走过的光程不相等。
(C)传播的路程不相等,走过的光程相等。
(D)传播的路程不相等,走过的光程不相等。
解:光在某媒质中的几何路程r与该媒质的折射率n的乘积 nr
r2
r1
(2 j 1)
2
(暗纹)
相长
r r 常量,干涉花相样长 为双叶螺旋双 曲面
2
1
同级条纹为旋 转双曲面
相长
如果是双缝干涉,则 相长
屏上条纹是直纹。
相长 如果s1s2相差不恒定, 则条纹是高速变化。 相长 无条纹.
1.3 分波面
双光束干涉
p
分波面法(杨氏)
S*
分振幅法
S*
分振动面法(5.9)
r2
s2
E1 A01 cos[t 10]
E2 A02 cos[t 20] s1
r1
P
r2
两波传至P点,引起两个振动:
s2
E1 p
A01
cos[(t
r1 ) v1
10 ]
E2 p
A02
cos[(t
r2 v2
) 20 ]
1
2
( r2
v2
r1 v1
)
(10
20 )
( r2
v2
r1 v1
) (10
二、干涉图样的形成:
then: I A2 A2 A2 2A A cos
1
2
12
2
1
大学物理光的干涉和衍射

7
2.光程差—两束光光程之差
s1
r1
n1
p
n2 s2
r2
=n1r1- n2r2
图20-1
p
s1 s2
S1p= r1 S2p= r2
= (r1-e1 +n1e1) - (r2-e2 +n2e2) 图20-2
8
3.两束光干涉的强弱取决于光程差,而不是几 何路程之差
解 凡是求解薄膜问题应先求出两反射光线的光 程差。对垂直入射,i =0,于是
反 2e
n22 n12sin2i
+ 半 = 2en2
(0, )
2
无反射意味着反射光出现暗纹,所以
e 1.25 1.50
1
反
2en2
(k
) 2
(k=0,1,2,……)
n2=1.25(薄膜的折射率);要e最小,k =0
e =1200Å=1.2×10-7m
这对讨论光经过几种媒质后的相干叠加问题,是很不 方便的。为此引入光程的概念。
6
n=c/
= /n
1.光程
设经时间t,光在折射率为n媒质中通过的几何
路程为r,则nr称为光程。
显然,光程 nr=n t =c t 。
光程的物理意义: 光程等于在相同的时间内光在 真空中通过的路程。
引入光程概念后,就能将光在媒质中通过的几何
代入:d=0.25mm, L=500mm, 2=7×10-4mm , 1= 4 ×10-4mm得:
x =1.2mm 18
例题20-2 将双缝用厚e、折射率分别为n1=1.4、 n2=1.7的透明薄膜盖住,发现原中央明级处被第五级 亮纹占据,如图20-5所示。所用波长=6000Å,问:原中
光波的相干叠加

二、分波阵面干涉的其它一些实验
光栏
1、菲涅耳双面镜实验: 菲涅耳双面镜实验:
d
S1
S2
S
M1
M2
W
2、 菲涅耳双棱镜实验 、
x o W'
W
θ
结论:屏幕上 点 结论:屏幕上O点 S1 在两个虚光源连线 d S S2 的垂直平分线上。 的垂直平分线上。 它们也是分波前双 D 光束干涉。 光束干涉。是不定 域干涉。 域干涉。
n1 n2 A n1
i
N
C
d
1
γ
B
n1
i
A
N C
2
n
n1
B
11
被薄膜的上下表面反射的两束光的光程差为: 被薄膜的上下表面反射的两束光的光程差为:
{
d C AB = BC = AC = 2dtg r n A cos r n1 r B o AN = AC cos(90 − i ) = AC sin i n两侧介质相同,薄膜 两侧介质相同, 两侧介质相同 n1 sin i = n sin r 上下表面反射的两束 λ 2 2 2 光中一束有半波损失 光中一束有半波损失 δ = 2d n − n1 sin i + 2
L
光栏
M
D0
7
3. 洛埃镜实验
当屏幕W移至 处 当屏幕 移至B处, 移至 从 S 和 S’ 到B点的 点的 光程差为零, 光程差为零,但是 观察到暗条纹, 观察到暗条纹,验 证了反射时有半波 损失存在。 损失存在。
光栏
S d
S'
p p'
Q'
A
M
B
Q
L
W
4.半波损失 半波损失
波的相干叠加

波的相⼲叠加波的独⽴性和叠加性⼏列波相遇于同⼀区域,只要振动不是⼗分强烈,各波可以保持各⾃的频率、振幅和振动⽅向等特性,按照本⾝原来的传播⽅向继续前进,彼此不受影响,这就是波的独⽴性。
在相遇区域,总的振动是分振动的线性叠加。
两列或两列以上的波,如果波频率相等,在观测时间内波动不中断,⽽且在相遇处振动⽅向⼏乎沿同⼀直线,那么叠加后的合振动可能在某些地⽅加强,某些地⽅减弱,这种现象称为⼲涉。
振动强度的分布称为⼲涉图样,或⼲涉花样。
⼲涉是波独有的⾏为,表明实物物体的运动与波动是完全不同的。
两个运动的实物物体——⽐如两列⽕车——不可以毫不⼲扰地彼此穿越。
波的独⽴性和叠加性并不是总能成⽴的,当波的强度⾮常⼤时,独⽴性和叠加性可能会失效。
相⼲与不相⼲叠加考虑频率相同,振动⽅向相同,具有恒定初始相位的两列波的叠加。
设这两列波从空间两定点S 1和S 2发出,波源的振动可分别表⽰为ψ01=A 1cos ωt +φ01\begin{equation }\psi_{02}=A_2\cos\left (\omega t+\varphi_{02} \right)\end{equation }其中φ01和φ02分别是两波源振动的初相位。
两列波同时到达空间⼀点P 处,P 点到两波源的距离分别是r 1和r 2,波速分别为v 1和v 2,如下图所⽰,则P 点处的振动为ψ1=A 1cos ωt −r 1v 1+φ01=A 1cos ωt +φ1\begin{equation }\psi_2=A_2\cos\left [\omega\left (t-\frac{r_2}{v_2}\right)+\varphi_{02} \right ]=A_2\cos\left (\omega t+\varphi_{2} \right)\end{equation }其中φ1=−ωr 1v 1+φ01,φ2=−ωr 2v 2+φ02,为两个振动的相位。
光学第11讲

第四章
光的干涉
水膜在白光下
白光下的肥皂膜
蝉翅在阳光下
蜻蜓翅膀在阳光下
白光下的油膜
肥皂泡玩过吗? 肥皂泡玩过吗
测油膜厚度
平晶间空气隙干涉条纹
等倾条纹
牛顿环(等厚条纹) 牛顿环(等厚条纹)
ξ1
光是一种电磁波
相干光
E = E0 cos ω (t r ) v
H = H 0 cos ω (t r ) v
由矢量合成: 由矢量合成:
E = E1 + E2
将上式平方后,在观察的时间内求时间平均值: 将上式平方后,在观察的时间内求时间平均值:
E
2
= E
2 1
+ E2 + 2 E1 i E2
2
E
2
= E
2 1
+ E2 + 2 E1 i E2
2
(1)两光波的光矢量互相垂直 ( E1 ⊥ E2 ) 时 )
习题3.5: 习题3.5:一个波片堆由十块平行平面熔石英玻璃板 3.5 互相平行放置而组成.已知熔石英的折射率为1.45 1.45. 互相平行放置而组成.已知熔石英的折射率为1.45. 求自然光以布儒斯特角入射,经波片堆透射后,光的 求自然光以布儒斯特角入射,经波片堆透射后, 偏振度为多少? 偏振度为多少?
பைடு நூலகம்
π Ex = AP cos ωt E y = AS cos ωt 2 由于是圆偏振光,上式中A 由于是圆偏振光,上式中AP=AS.
由菲涅耳反射折射公式可知,入射光以30° 由菲涅耳反射折射公式可知,入射光以30°角入 30 经过玻璃表面反射后: 射,经过玻璃表面反射后:
rP < rS
′ ′ AP < AS
光波的相干叠加

n1 n2 n1
i
N
C
d
1
A
B
n1
i
A
N
2
C
n
n1
B
11
被薄膜的上下表面反射的两束光的光程差为:
d C AB BC AC 2 dtg r n A cos r n1 r B AN AC cos( 90 i ) AC sin i n两侧介质相同,薄膜 n sin i n sin r 1 上下表面反射的两束 光中一束有半波损失 2 2 2 2 d n n i 1sin 2
S1
S d
r1
P x
x sin tg L
代入(1)、(2)式,可得
r2
O L
S2
L 明纹中心的位置: x k d
k 0 , 1 , 2 ,
L 暗纹中心的位置: x ( 2 k 1 ) 2 d
相邻两明纹或暗纹间的距离为: x L
k 1 , 2 , 3 ,
d
5
干涉条纹的特点
1. 是一组平行等间距的明、暗相间的直条纹。 2. 干涉条纹不仅出现在屏上,凡是两光束重叠的区域都存在干 涉,故杨氏双缝干涉属于非定域干涉。
3. 当D 、 λ一定时,Δx与d成反比,d越小,条纹分辨越清。
4. Δx与λ成正比,用白光做光源时,除中央明纹是白光外,其 它各级条纹是彩色条纹,紫在内红在外;不重叠的称为完整的 光谱。(k+1)Dλ 1/d≤kDλ2/d x 5.λ 1与 λ2为整数比时,某些级次的条 纹发生重叠。 k1 λ 1=k2 λ2 k 1 k 讨论题: 1. 如果用两个灯泡分别照亮S1、S2缝,能否看到干涉条纹? 2. S1缝后贴一红色玻璃纸,S2缝后贴一绿色玻璃纸,能否看到 干涉条纹? 3. 在S1 上覆盖一较厚的透明介质片对实验结果有何影响?
物理光学3光的干涉30课件1

x m D
d
I
-4
e- 2
m-1
0
e2
4
m
mm++12
在杨氏实验中: d D
y
条纹的间隔: e
S1
e 是一个具有普遍意义
S
O
S2
d
的公式,适合于任何干涉系统。
会聚角 x
r1
r2
D
y P(x,y,D) x
z
5、干涉条纹间隔与波长
条纹的间隔:e
条纹间隔 e , e 1 。
S线光源,G是一个遮光屏,其上有两条与S平行的狭缝S1、 S2,且与S等距离,因此S1、S2 是相干光源,且相位相同;S1、 S2 之间的距离是d ,到屏的距离是D。
G
r1
P
S1 SS d
r2
x O
S2
D
纹干 涉
I
光
条
强
分
布
同方向、同频率、有恒定初位相差的两个单色光源所 发出的两列光波的叠加。
1、干涉条纹代表着光程差的等值线。 意一点到两个光源
的光程差是恒定的。
2、相邻两个干涉条纹之间其光程差变化
量为一个波长,位相差变化2。
4、干涉条纹的间隔
1 .0
条纹间隔:
0 .8
0 .6
D
DD
0 .4
e (m 1) m
d
dd
0 .2
0 .0
定义:两条相干光线的夹角为相 干光束的会聚角,用表示。
两个频率相同的钠光灯不能产生干涉现象,即使是同一 个单色光源的两部分发出的光,也不能产生干涉。
无干涉现象
两个完全独立的没有关联的光波无论如何不会产生干涉,而 只有当两个光波有紧密关联或当两个光波是由同一光波分离出 来时,才会发生干涉。(从光源本身的发光特性来解释)
1-2 1-3波动的独立性、叠加性

next
'2 ' ' I A1 A '2 2 2 A 1 A 2 cos cos
k (r2 r1 )
11
12
光强极大的点满足: =2j
r2-r1=j
光强按余弦函数 S1 的形式变化
S2
所对应的点的集合是一组旋转双曲面。
E的振幅
பைடு நூலகம்
三个条件
且:2) 角频率 1 = 2 = (推出|k1|=|k2|= /v) 的关系?
没有干涉场分布。
next
这三个条件称为相干条件。
next
1
1 1t k 1 r1 1 , 2 2 t k 2 r 2 2
2 2A1 A2 cos(1 2 ) I A1 A2 2
4
按波叠加原理: E=E E E1 E 22 1+E 2 2=2<E·E> 总场的光强: I I=A A 2 EE
E E ( E1 E 2 ) ( E1 E 2 ) = E1 2 + E2 2 +2 ( AA 1 1A 2 2 ) cos 1cos 2
7
I I 1 I 2 2 I 1I 2 cos θ cos Δφ
8 ( k 2 r2 k 1 r1 ) ( 1 2 )
I 随变化, 与r2,r1有关,
因此,空间各点光强一般情况下是不同的。
r1 r2
2.干涉光强的分布 设 A 1与 A 2的夹角为 , 令:= 1- 2
S1 S2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A12A222A1A2cos2(1)
4
初相位由下式决定: tg A A 11cso i n 1 1s A A 2 2c sio n2 2s
因为振动的强度正比于振幅的平方,一般情况下 两个振动叠加时,合振动的强度不等于分振动强度 之和。
物理科学与信息工程学院 2
设两个沿着同一直线振动的简谐振动,其频率相 同,但相位不同,如下式所示:
E 1 A 1 co t s 1 )
E 2 A 2 co t s 2 )
由于振动方向相同,叠加后可以为:
E E 1 E 2 A c t o s
合振动的振幅A为:
A 2 A 1 2 A 2 2 2 A 1 A 2 co 2 1 s
能够观察到干涉现象的条件: ①光源的相干性; ②接收器的时间响应能力。
光源:早期光的干涉实验使用的大都是带虑色片的 普通钨丝灯单色性比较差,相干性也很差。
物理科学与信息工程学院 16
自1960年激光出现以后,使光源的相干性大大提高, 从而使得光的干涉现象较易观察到。
接收器:较早以前光的干涉现象通常用人眼进行观 察。人眼的响应时间约为0.1s。感光胶片的响应时间一 般不超过毫秒量级。
粗略的讲,原子(或分子)每次发射的光波的波列都是有 限长的,波列的长度与它们所处的环境有关,受其他原子作 用越强,发射波列越短。即使在稀薄的气体中,外界作用可 忽略情况下,发射的波列持续时间,也不会大于10-8秒。
物理科学与信息工程学院 14
其次,普通光源发光是随机过程,每个原子(或分子)先 后发射的不同波列,以及不同原子发射的各个波列,彼此间 在振动方向和相位上没有什么联系.因此普通光源发光,是 不相干的。即普通光源是非相干光源。
0
1 0 A 1 2 A 2 2 2 A 1 A 2 co 2 s 1 )d ( t
A 1 2 A 2 2 2 A 1 A 210 co 2 s1 )( dt
物理科学与信息工程学院 6
IA12A222A1A21 0c os2 (1)d t
I1I22
1
I1I2
c
0
os2 (1)dt
本节结束
物理科学与信息工程学院 18
11
多个振动叠加时,情况也是一样,设有几个同频 率的振动,振幅都等于A,振动方向都沿着同一直线。 如果它们是相干叠加的,则
那么合振动强度介于 Imax (n1A )2n2A 1 2和 Imin=0 之间。
如果它们是非相干叠加,那么合振动强度应为
I nA12
前面介绍的是电磁振动的叠加问题,由光的电磁 理论,光是波长较短的电磁波,光波在传播过程中 具有独立性。
物理科学与信息工程学院 1
在现实生活中,经常会遇到这种情况,例如: 两盏灯同时照射到同一平台,总是照度到处都加 强了,其值等于两盏灯照度之和,没有一处照度 减弱。观察不到干涉图样,这样的两波称为不相 干。这样的叠加称为非相干叠加。
波动是振动在空间的传播,因此两列光波的叠 加问题可以归结为讨论空间任一点电磁振动的叠 加,为什么两波相遇进行叠加时会出现相干叠加 或非相干叠加?为此我们回顾一下简谐振动的合 成问题。
则合振动的强度为
Im in (A 1A 2)2
合振动平均强度达到最小值,称为干涉相消。
如果相位差为其他值,则合振动的强度介于Imax和
Imin之间。
若A1=A2,则
I 2 A 1 2 1 co 1 2 s )) (4 A 1 2 co 2 2 s 1 )(
4A12
co2s
2
物理科学与信息工程学院
机械波与光波的差异:
在力学、声学现象和微波技术中,独立振源的振动 在观察时间内通常是持续进行的,是不中断的,频率 相对较低,它们之间的相位差能够保持不变。所以独 立的机械波振源一般是相干的,因此通常干涉比较容 易实现。
物理科学与信息工程学院 15
但是,在光学现象中,由于原子辐射的复杂性,在 不同瞬时所得的干涉图样变化的非常快而不规则。使 得人眼和通常的探测仪器都观察不到干涉现象。
随着快速光电接收器件的出现使接收器的响应时间 从0.1s缩短到微秒、纳秒甚至皮秒量级。
用这样的接收器去观测光的干涉现象,就可以观测 到干涉图样稳定时间较短的干涉现象。
物理科学与信息工程学院 17
2. 相干光获得方法 分波阵面法: 杨氏双缝干涉、菲涅耳双棱镜干涉、菲涅耳双面镜
干涉、劳埃德镜干涉等
分振幅法: 等倾干涉、等厚干涉等
物理科学与信息工程学院 12
即从各种物体发出的光在空间相交,并不影响各光 束的独立传播,因此关于电磁振动叠加的讨论,对光 振动在空间任一点的叠加也同样是适用的。
二、相干条件 根据前后的分析,可以得到两列或两列以上的波
在空间一点相遇能产生干涉(或相干叠加)的条件为:
(1)频率相同; (2)两振动的相位差保持不变。 (3)振动方向相同或至少具有相同振动分量
2 A 1 A 2co2 s1 ()称为干涉项。
如果两振动相位差
2 1 2 j(j 0 ,1 ,2 ,3 .....)
则合振动的强度为
Ima x(A 1A 2)2
合振动平均强度达到最大值,称为干涉相长。
物理科学与信息工程学院 10
如果两振动相位差
2 1 ( 2 j 1 )(j 0 ,1 ,2 ,3 ....
1. 非相干叠加
如果在观察时间内,振动时断时续,(光源的发生 就属于这种情况),以至它们的初相位各自独立地做 不 规则的改变,概率均等在观察时间内多次经历从0 到2之间一切可能值。
物理科学与信息工程学院 7
即
21f(t)
则
1
cos2 (1)d t 0
0
因此合振动的平均光强为
IA 2A 1 2A 2 2
则上式末项的积分值为 :
10cos2(1)dtco2s(1)
则合振动的平均强度为:
I A 2 A 1 2 A 2 2 2 A 1 A 2co 2 s1 ) (
物理科学与信息工程学院 9
合振动的平均强度为:
I A 2 A 1 2 A 2 2 2 A 1 A 2co 2 s1 ) (
第五章 光的干涉
(Interference of light)
§5.2 相干叠加与非相干叠加 相干条件
一、相干与不相干叠加
如果两波频率相等,在观察时间内波动不中断,而且在相遇 处振动方向几乎沿着同一直线,那末它们叠加后产生的合振动 可能在有些地方加强,在有些地方减弱。
这种强度按照空间周期性变化的现象称为干涉。我们说两波 相干,这样的叠加称为相干叠加。在叠加区域内,振动强度出 现周期性分布的整体图像,称为干涉图样。
物理科学与信息工程学院 3
如果用复振幅表示,则:
E 1 A 1 co t s 1 )
E 2 A 2 co t s 2 )
叠加后可以为:
EE1E2
Acost
E ~ 1(P )A 1 ei1 E ~ 2(P )A 2 ei2
E~E~1E~2 A1ei1 A2ei2
合振动的振幅A为:A2E ~•E ~
物理科学与信息工程学院 13
三、相干光的获得
1.光源的发光机制
光的干涉无可辩驳地肯定了光的波动性,但通常情况下, 当两个光源同时照明同一区域时,观察不到干涉图样,说明 通常两个独立的普通光源之间的叠光源呢?这 是由它们的发光机制决定的。
对于光波来讲,由于光频很高,而探测器都有一 定的响应时间(人眼约0.1秒,光电探测仪器最快约 2ps),实际观察到的总是在较长时间内的平均强度。
物理科学与信息工程学院 5
在某一时间间隔内 (其值远大于光振动的 周期
T,例如可见光波段,T约为10-15s),则合振动 的平均相对强度为:
IA21 A2dt
合振动的平均强度等于分振动强度之和。
其干涉项的平均值为0,两振动叠加后没有强度减 弱的情况,此即非相干叠加。
物理科学与信息工程学院 8
2. 相干叠加
如果在观察时间内,两电磁振动各自连续进行, 并不中断(这种观察在光学中很少遇见) 。
它们初相位差,也就是说任意时刻的相位差, 2 1
始终保持不变,与时间无关。
