光学——第2章题解
《应用光学》第2章课后答案全文

12. 由两个透镜组成的一个倒像系统,设第一组透镜的焦距 为f1′,第二组透镜的焦距为f2′,物平面位于第一组透镜 的物方焦面上,求该倒像系统的垂轴放大率。
解:
1
1
1
1
F2
1
1
第一组透镜
第二组透镜
1
第二组透镜
13. 由两个同心的反射球面(二球面球心重合)构成的光学系 统,按照光线反射的顺序第一个反射球面是凹的,第二个 反射球面是凸的,要求系统的像方焦点恰好位于第一个反 射球面的顶点,求两个球面的半径r1,r2和二者之间的间隔 d之间的关系。
B′
面,如图示.
l ′ = 2f′
4 试用作图法对位于空气中的正透镜组( f 0 )分别求 下列不同物距的像平面位置.
l = −f′
B
……
F
F′
A
H H′
像平面在像 空间无限远 处.
l′=∞
4 试用作图法对位于空气中的正透镜组( f 0 )分别求 下列不同物距的像平面位置.
l f' 2
B′
r1 无穷远物点
r2
r1/2
最终像点
11 2
l2 l2 r2
l2
l2
2 r2
(l2l2 )
14. 假定显微镜物镜由相隔20mm的两个薄透镜组构成,物平 面和像平面之间的距离为180mm,放大率β=-10×,要求近 轴光线通过二透镜组时的偏角Δu1和Δu2相等,求二透镜 组的焦距。
y n1u1 u1 10
l = −f′
B
……
F′
F
H H′
A
像平面在像 空间无限远 处.
5 试用作图法对位于空气中的负透镜组( f 0 )分别求 下列不同物距的像平面位置.
光学第二章习题解答

∆y = y2 − y1 ≈ 2 f ′
λ
b
− f′
λ
b
= f′
λ
b
∆y ⋅ b 0.02 × 0.885 ɺ λ= = = 5900 A f′ 300
(2)波长为 波长为0.1nm的x射线时,相邻最小值间的距离为 射线时, 波长为 的 射线时
′λ 300 × 0.1×10−9 f ∆y = = 0.02 b −6 −4 = 1.5 × 10 m = 1.5 × 10 cm
主焦点
还有次焦点: 还有次焦点:± f ′ /3,
± f ′ /5, ± f ′ / 7⋯
故:光强极大值出现在轴上 1/3m,1/5m,1/7m……1/(2k+1)m等处 , , 等处
2.6 波长为 的点光源波带片成一个像点,该波带 波长为λ的点光源波带片成一个像点 的点光源波带片成一个像点, 个透明奇数半波带(1, , )。另外 有100个透明奇数半波带 ,3,5 ……199)。另外 个透明奇数半波带 )。 100个不透明偶数半波带。比较用波带片换上同样焦 个不透明偶数半波带。 个不透明偶数半波带 距和口径的透镜时像点的强度比I: 距和口径的透镜时像点的强度比 :I0 解:(1) 只有 ) 只有100个透明奇数半波带透过 个透明奇数半波带透过
∵
θ3 < θ 2
∴
二级和三级光谱部分重叠 二级和三级光谱部分重叠
2.14 用波长为 用波长为589nm的单色光照射一衍射光栅, 的单色光照射一衍射光栅 的单色光照射一衍射光栅, 其光谱的中央最大值和第二十级主最大值之间的衍 射角为15 10′。试求该光栅1cm内的缝数是多少? 15° cm内的缝数是多少 射角为15°10′。试求该光栅 cm内的缝数是多少? 解: 由光栅方程 d sin θ = jλ
物理光学第二章答案

第二章光的干涉作业1、在杨氏干涉实验中,两个小孔的距离为1mm,观察屏离小孔的垂直距离为1m,若所用光源发出波长为550nm和600nm的两种光波,试求:(1)两光波分别形成的条纹间距;(2)两组条纹的第8个亮条纹之间的距离。
2、在杨氏实验中,两小孔距离为1mm,观察屏离小孔的距离为100cm,当用一片折射率为1.61的透明玻璃贴住其中一小孔时,发现屏上的条纹系移动了0.5cm,试决定该薄片的厚度。
3、在菲涅耳双棱镜干涉实验中,若双棱镜材料的折射率为1.52,采用垂直的激光束(632.8nm)垂直照射双棱镜,问选用顶角多大的双棱镜可得到间距为0.05mm 的条纹。
4、在洛埃镜干涉实验中,光源S1到观察屏的垂直距离为1.5m,光源到洛埃镜的垂直距离为2mm。
洛埃镜长为40cm,置于光源和屏的中央。
(1)确定屏上看见条纹的区域大小;(2)若波长为500nm,条纹间距是多少?在屏上可以看见几条条纹?5、在杨氏干涉实验中,准单色光的波长宽度为0.05nm,平均波长为500nm,问在小孔S1处贴上多厚的玻璃片可使P ’点附近的条纹消失?设玻璃的折射率为1.5。
6、在菲涅耳双面镜的夹角为1’,双面镜交线到光源和屏的距离分别为10cm 和1m 。
设光源发出的光波波长为550nm ,试决定光源的临界宽度和许可宽度。
7、太阳对地球表面的张角约为0.0093rad ,太阳光的平均波长为550nm ,试计算地球表面的相干面积。
8、在平行平板干涉装置中,平板置于空气中,其折射率为1.5,观察望远镜的轴与平板垂直。
试计算从反射光方向和透射光方向观察到的条纹的可见度。
9、在平行平板干涉装置中,若照明光波的波长为600nm ,平板的厚度为 2mm ,折射率为1.5,其下表面涂上高折射率(1.5)材料。
试问:(1)在反射光方向观察到的干涉圆环条纹的中心是亮斑还是暗斑?(2)由中心向外计算,第10个亮环的半径是多少?(f=P P ’20cm)(3)第10个亮环处的条纹间距是多少?10、检验平行平板厚度均匀性的装置中,D是用来限制平板受照面积的光阑。
工程光学习题参考答案第二章理想光学系统
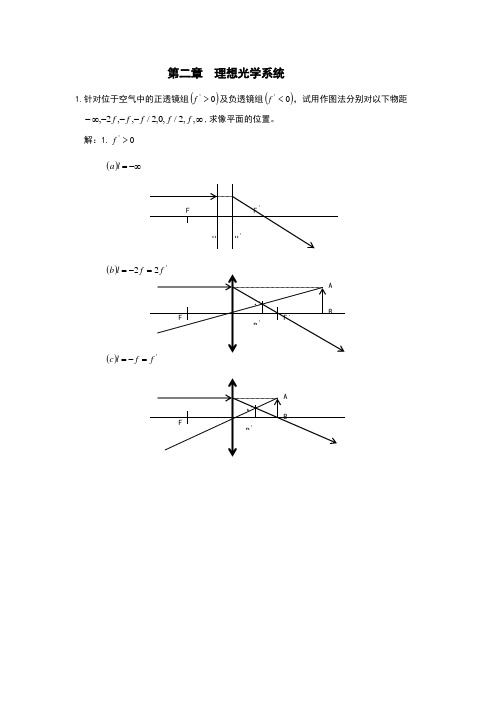
第二章 理想光学系统1.针对位于空气中的正透镜组()0'>f 及负透镜组()0'<f ,试用作图法分别对以下物距 ∞---∞-,,2/,0,2/,,2,f f f f f ,求像平面的位置。
解:1.0'>f ()-∞=l a()'2f l b -=()f f l c =-=()/f l d -=()0=l e()/f l f =')(f f l g -=='22)(f f l h -==+∞=l i )(2.0'<f -∞=l a )(l b )(=l c =)(/)(f l d -=0 el(=)f=l2/ (f)()fg=l(=h)ll i)(+∞=2. 已知照相物镜的焦距f’=75mm,被摄景物位于(以F 点为坐标原点)=x ,2,4,6,8,10,m m m m m -----∝-处,试求照相底片应分别放在离物镜的像方焦面多远的地方。
解: (1)x= -∝ ,xx ′=ff ′ 得到:x ′=0 (2)x ′= (3)x ′= (4)x ′= (5)x ′=(6)x ′=3.设一系统位于空气中,垂轴放大率*-=10β,由物面到像面的距离(共轭距离)为7200mm , 物镜两焦点间距离为1140mm 。
求该物镜焦距,并绘出基点位置图。
解:∵ 系统位于空气中,f f -='10''-===ll y y β 由已知条件:1140)('=+-+x f f7200)('=+-+x l l解得:mm f 600'= mm x 60-=4.已知一个透镜把物体放大*-3投影到屏幕上,当透镜向物体移近18mm 时,物体将被放大*-4,试求透镜的焦距,并用图解法校核之。
解:方法一:31'11-==l l β ⇒ ()183321'1--=-=l l l ①42'22-==l l β ⇒ 2'24l l -= ② 1821+-=-l l ⇒ 1821-=l l ③ '/1/1/11'1f l l =-'/1/1/12'2f l l =-将①②③代入④中得 mm l 2702-= mm l 1080'2-= ∴ mm f 216'=方法二: 311-=-=x fβ 422-=-=x fβ ⇒ mm f 216-= 1812=-x x方法三: 12)4)(3(21''=--==∆∆=ββαnn x x2161812'-=⨯=∆x''fx -=β143''''2'121=+-=∆=+-=-∴fx fx x ββ mm x f 216''=∆=∴5.一个薄透镜对某一物体成实像,放大率为⨯-1,今以另一个薄透镜紧贴在第一个透镜上,则见像向透镜方向移动,放大率为原先的3/4倍,求两块透镜的焦距为多少 解:⇒ 2'21'1/1/1/1/1l l l l -=- ④6.有一正薄透镜对某一物成倒立的实像,像高为物高的一半,今将物面向物体移近100mm , 则所得像与物同大小,求该正透镜组的焦距。
南开考研光学专业习题与解答第二章

第二章 光波的基本概念例题(1) 沿x 轴正方向传播的两列平面波, 波长分别为5890 和5896 . t=0时刻两波的波峰在O 点重合,试问(2) 自O 点算起,沿传播方向多远的地方两波列的波峰还会重合?在O 点由t=0算起, 经过多长时间以后, 两列波的波峰又会重合?解 两列波t =0时刻在O点波峰与波峰相重合, 设传播距离为x 时波峰与波峰又重合,则距离x 必是两波长(1=5890 和(2=5896 的公倍数, 即,由上式294531⨯=∆=n n k λλ. 式中k 和n 都是整数, 取n=3, k=2945, 得最小公倍数.即两波传播 距离时波峰与波峰再重合. 而且, 以后每传播距离 , 两波的波峰和波峰都会重合, 这是光波的空间周期性决定的.(2)光波具有时间周期性, 两光波的时间周期分别为 和 .两光波在O点t =0时刻波峰与波峰相重合, 当扰动时间间隔是这两个周期的公倍数时, 波峰与波峰会再重合.仿照上面的讨论, 可以求出这个时间的公倍数.但是简单的方法是, 利用时间周期和空间周期的相互关系, 可以直接求得两波峰再次相重合的时间间隔为7879.5≈=cx t m m (微微秒) 地球表面在垂直于光传播方向每平方米接收到的太阳光功率约为 1.33kW, 试计算地球表面的电场强度的振幅值.解 题中已给出太阳光在地球表面上的光强为I=1.33kw, 光强与振幅值的关系为,式中 是空气的折射率, c 为光速, 为真空中介电常数, 故地球表面电场强度的振幅值为2.1 (伏/米).若人眼和光电探测器对光信号的响应时间分别为0.1秒和10-9秒, 在这两段时间中光扰动分别经历了多少个周期? (光波波长取550纳米)答 可见光波段的频率数量级为 Hz, 在人眼可分辨的最小时间间隔(时间响应能力)0.1s 内, 光扰动经历了 次.光电探测器的响应能力为 s, 在这个可分辨的最小时间间隔内光扰动也经历了 次.人眼和光电探测器的时间响应能力远远大于光振动的周期,因此, 目前的接收器不能进行对光频的直接测量.一列沿z 方向传播的椭圆偏振光, 可以表示为j t kz E i t kz E t z E )4/cos()cos(),(00πωω--+-=求:(1)该椭圆的方程;(2)确定该椭圆的长轴的方向;该椭圆的长半轴和短半轴.解(1)该椭圆偏振光是沿z轴传播的, 在xy平面内的电振动分量为,.Y方向电振动相位超前x方向振动相位(/4. 将上面两方程消去t, 得电矢量端点轨道方程,(2)椭圆内切于边长为2 的正方形(计算题2.4解图), 由解析几何公式, 椭圆的半长轴a和半短轴b分别由下式给出:,.,,(3)椭圆长轴与x轴的夹角(满足,故计算题2.4解图选择题(1)下列四种说法哪一种对?光在折射率较大的介质中传播较慢.(2)光在折射率较大的介质中折射角较大.(3)光在折射率较大的介质中的振动频率变快.2.1光在折射率较大的介质中波长变长.(1)判断下列说法的正误.(2)相干叠加服从光波的叠加原理, 非相干叠加不服从光波的叠加原理.(3)光强可以直接相加就服从光波的叠加原理, 否则就不服从.2.2两列波相干叠加时光强不能直接相加, 此时波的独立传播定律不成立.2.3椭圆偏光是同频率、有确定位相关系的两个电振动的叠加, 是相干叠加.(1)下面三种说法哪种对?(2)用旋转的振幅矢量图所描述的量肯定是矢量.2.4振幅矢量是矢量, 它在轴向的投影值所描述的振动量可以不是矢量.2.5振幅矢量不是矢量, 它只是一种描述简谐振动值的工具.(1)下列四种说法孰是孰非?(2)有相同的振幅就有相同的光强.(3)振幅较大者, 其光强较大.2.6分别位于空气和水中的振幅相等、但光强不等的两点, 空气中的光强较强.(1)在同一介质中的不同两点, 若光强相同, 则振幅一定相同.(2)两个传播方向一致、频率相同、振幅相等、振动方向互相垂直的线偏光, 可以合成:(3)自然光(4)线偏振光(5)圆偏振光(6)椭圆偏振光(1)两个振幅相等、频率相同、传播方向一致、有相位关系的圆偏振光, 一个是右旋, 一个是左旋, 则可以组合成:(2)线偏振光.(3)圆偏振光(4)椭圆偏振光(5)自然光。
物理光学 梁铨廷 答案

第一章光的电磁理论1.1在真空中传播的平面电磁波,其电场表示为Ex=0,Ey=0,Ez=,(各量均用国际单位),求电磁波的频率、波长、周期和初相位.解:由Ex=0,Ey=0,Ez=,则频率υ===0。
5×1014Hz,周期T=1/υ=2×10-14s,初相位φ0=+π/2(z=0,t=0),振幅A=100V/m,波长λ=cT=3×108×2×10—14=6×10—6m。
1。
2。
一个平面电磁波可以表示为Ex=0,Ey=,Ez=0,求:(1)该电磁波的振幅,频率,波长和原点的初相位是多少?(2)波的传播和电矢量的振动取哪个方向?(3)与电场相联系的磁场B的表达式如何写?解:(1)振幅A=2V/m,频率υ=Hz,波长λ==,原点的初相位φ0=+π/2;(2)传播沿z轴,振动方向沿y轴;(3)由B =,可得By=Bz=0,Bx=1。
3.一个线偏振光在玻璃中传播时可以表示为Ey=0,Ez=0,Ex=,试求:(1)光的频率;(2)波长;(3)玻璃的折射率。
解:(1)υ===5×1014Hz;(2)λ=;(3)相速度v=0.65c,所以折射率n=1.4写出:(1)在yoz平面内沿与y 轴成θ角的方向传播的平面波的复振幅;(2)发散球面波和汇聚球面波的复振幅。
解:(1)由,可得;(2)同理:发散球面波,汇聚球面波。
1。
5一平面简谐电磁波在真空中沿正x方向传播。
其频率为Hz,电场振幅为14。
14V/m,如果该电磁波的振动面与xy平面呈45º,试写出E,B表达式。
解:,其中===,同理:。
,其中=。
1。
6一个沿k方向传播的平面波表示为E=,试求k 方向的单位矢。
解:,又,∴=.1。
9证明当入射角=45º时,光波在任何两种介质分界面上的反射都有.证明:====1。
10证明光束在布儒斯特角下入射到平行平面玻璃片的上表面时,下表面的入射角也是布儒斯特角。
光学作业答案

I = 0.37% ,此时接近消反射。 I0
2π λ0 λ0 = π , λ0 = 500nm λ 2 λ
(2)反射两光束相位差
δ=
2π
λ
2n 2 h =
将 λ = 400nm 和 λ = 700 nm 分别代入上式,得到相位差分别是 1.375πrad 和 0.7857πrad 20.砷化镓发光管制成半球形,以增加位于球心的发光区对外输出功率,减少反射损耗,已 知砷化镓发射光波长 930nm,折射率为 3.4,为了进一步提高光输出功率,常在球形表面涂 一层增透膜。 (1)不加增透膜时,球面的强度反射率多大? (2)增透膜折射率和厚度应取多大? (3)如果用氟化镁(1.38)作为增透膜,能否增透?强度反射率多大? (4)如果用硫化锌(2.35) ,情况又如何? 解:
此光学系统成像在 L1 之右 10cm 处。
, s1, s2 10 10 = − = −1 , V2 = − = − = 2, 横向放大率分别为 V1 = − −5 s1 10 s2
总放大率 V = V1 • V2 = −2 27.用作图法求本题各图中的 Q 像。 (a)
(b)
(c)
(d)
35.(1)用作图法求图中光线 1 共轭线 (2)在图上标出光具组节点 N,N’位置
与屏幕交点(零级)随之移动,即以 M 为中心转了角 β ≈ δs / B ,反映在屏幕上零级位移
C δs ,即幕上条纹总体发生一个平移。 B (5)设扩展光源 b,即其边缘两点间隔 δs = b ,若这两套条纹错开的距离(零级平移量) δx = Δx ,则幕上衬比度降为零,据此有, B+C C δx = b , Δx = λ 2aB B 令 δx = Δx ,
36.已知 1-1’是一对共轭光线,求光线 2 的共轭线。
光学教程第二版习题答案(一至七章)

∴ d1
=
h1 − h2 tan u1′
= 1.5 −1 0.015
= 33.33mm
tan u2 ′ = tan u2
+
h2 f 2′
= 0.015 +
1 = 0.011
− 250
∴d2
=
h2 − h3 tan u2 ′
1 − 0.9 =
0.011
= 9.091mm
2-13 一球形透镜,直径为 40mm,折射率为 1.5,求其焦距和主点位置。
= −200mm
lH
= dϕ2 ϕ
= 50 × 5 = −100mm − 2.5
2-11
有三个透镜,
f1′
= 100mm,
f2′
= 50mm,
f
′
3
=
−50mm,其间隔 d1
= 10mm,
d 2 = 10mm ,设该系统处于空气中,求组合系统的像方焦距。
解:设 h1 = 100mm, u1 = 0 ,则:
tan u3′
= tan u3 +
h3 f3′
= 2.8 +
62 − 50
= 1.56
∴组合系统的像方焦距为:
f
′=
h1 tan u3′
100 =
1.56
= 64.1mm
2-12
一个三 片型望远镜 系统,已知
f
′
1
= 100mm,
f
′
2
=
−250mm ,
f
′
3
= 800mm,入
射平行光在三个透镜上的高度分别为: h1 = 1.5mm, h2 = 1mm , h3 = 0.9mm ,试求合成
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
细丝习题2.11图第2章题解2.8解:(沈惠君等大学物理指导题P177) (1)由 λk dD x k =则 λd D x 1010±=± 故m 11.0105.510222020741010=⨯⨯⨯⨯==-=∆---λd D x x x (2)原坐标原点处是干涉的零级条纹,此处光程差为 021=-r r 当将上面一条缝上覆盖一薄片后,坐标原点处的光程差变为 21)1(r r e n -+- 则原点处光程差改变量是 λk e n =-)1( 得7106.6105.5158.1)1(67=⨯⨯⨯-=-=--λen k 即原零级条纹移到原第7级条纹处。
整个条纹向上移动。
2.9 解:(沈惠君等大学物理指导题P177)光线垂直照射在膜表面,两支反射相干光的光程差为ne 2,当相消干涉时,满足2)12(2λ+=k ne在可见光范围内,满足相消干涉的波长是nm 0051=λ与nm 7002=λ, 则有 2)12(211λ+=k ne ① 2)12(222λ+=k ne ②由于在此期间无其他相消波长,所以 121=-k k ③ ①比上② 得112122121=++λλk k 再将③代入 得3400070005000)(212211=+=-+=λλλλk由①得 m e 7710731.6210530.12132--⨯=⨯⨯⨯+⨯=2.10 解:(张三慧编著的大学物理学 P410)由光程差改变 λN L =2 得 mm N L 410349.512043220.022-⨯=⨯==λ 2.11解:(钟锡华等光学习题解P133)由劈尖等厚干涉条纹的特点,知相邻亮(或暗)条纹对应的厚度差为2λ;细丝所在处和劈尖棱边的条纹性质相同,故细丝 和棱边处的厚度差,即m D μλλ357.23.5894428=⨯===习题2.12图2.12解:(钟锡华等光学习题解P133)(1)由条纹间距与劈尖楔角的关系 l∆=2λθ又由实验装置知2G 和1G 的高度之差 θl d =∆ 故有μm 47.29105.023.589521=⨯⨯⨯=∆==∆-l l l d λθ 轻点待测块规一侧的平晶,若条纹间距密集了,说明劈尖楔角增大,由实验装置知,待测块规比标准件高度低; 若条纹稀疏了,说明楔角变小,则待测块规高于标准件。
(2)条纹间距不同,说明两块规顶端平面与平晶间的楔角不同。
即1G 、2G 上端面不平行。
T 和2G 间的干涉条纹间距小于T 和1G 间的干涉条纹间距,说明T 和2G 间的楔角大于T 和1G 间的楔角,则说明2G 的上端面向右有一个倾斜。
2.13 解:(高教社题库)设光源中的两种谱线的波长分别是λ和λλΔ+.由相干的基本条件知,在干涉仪的视场中会分别出现λ的一组干涉条纹和λλΔ+的一组干涉条纹.这两组条纹在视场中重叠.当处在零光程差时,各波长的零级条纹重合,其他级次条纹有微小的错位,所以在视场中还可看到清晰的干涉条纹.在移动M 1镜的过程中,两组条纹各级次都错开,所以逐渐模糊,当光程差改变到使λ的干涉最大与λλΔ+的干涉极小重叠时,视场最模糊.即当M 1移动距离为d 时,使两波长满足关系λk d =2 ①)Δ)(21(2λλ+-=k d ②视场最模糊.再继续移动M 1,当光程差的改变使得两个波长的干涉最大又一次在视场中重合,则又出现清晰的条纹. 即当M 1移动距离为d 时,使两波长满足关系λk d =2 ③ )Δ)(1(2λλ+-=k d ④则视场又一次清晰.(1) 由①②两式有 )Δ21(λλλ+-=k k 得 λλΔ221+=k(2) 由③④两式有 λλΔ1+=k 因为 λλΔ>> 所以 λλΔ=k 代入③式 λλΔ22=d 得 d 2Δ2λλ=0.6n m m 10610289.021*******182=⨯=⨯⨯⨯=--- (3)该光源是钠元素发的黄光(即钠D 双线).其中nm 0.589=λ,另一波长是nm 6.589Δ=+λλ。
2.14解:(钟锡华等光学习题解P145)(1)移动平面镜2M 后,中心吞(吐)了10环,说明中心处的光程差改变了10个波长,即2M 镜移动的距离为nm 29473.5895210=⨯==∆λe (2)初始时 中心亮环满足的光程差为 λm e =12 ① 视场边缘的亮环满足的光程差为 λ)12(cos 21-=m i e ② 移动2M 镜后,中心亮环满足的光程差为 λ)10(22-=m e ③ 视场边缘的亮环满足的光程差为 λ)15(cos 22-=m i e ④ 由第(1)的结果,知 λ521=-=∆e e e ⑤②/① 得 m m i 12cos -=⑥ ④/③ 得 1015cos --=m m i ⑦由⑥⑦ 得 17=m(3)2M 移动后,从中心向外数第5圈亮环的干涉级为 251017=--=k 2.15解:(钟锡华等光学习题解P147)(1)若反射镜移动了e ∆,条纹移动了N ∆条,则有关系式 2λN e ∆=∆两边被时间t ∆除,得 2λt N t e ∆∆=∆∆ 即 2λνυ⋅= 故 νυλ2= (2)s m /1526.0502μλνυ=⨯=⋅= (3)212332121,102.5)6.589100.58910(152)11(222ννλλυλυλυν<<⨯=-⨯=-=-=∆-Hz2.16解:(钟锡华等光学习题解P150)由法布里-珀罗干涉仪这样亮纹光程差λm k nh =2, 得 571050.21025002-⨯=⨯==nhk m λ观察屏2习题2.17图P习题2.20图由第10圈亮环满足的光程差λθ)10(cos 2-=m k nh ,得 λθnhk m 2)1(cos -=最终得9998.0210121022)10(cos ≈-=-=-=nh nh nh nh k m λλλλθ 第10圈的角直径为 81230.29998.0cos 22o o 1'==⨯=-θ 2.17解:(张三慧编著的大学物理学 P405) 由已知,cm D 50= mm d 4= 镜右边缘P 点是暗纹,右边缘到第一条明纹的距离是λd D x 2=∆7102.742500-⨯⨯⨯=m 5105.4-⨯=2.18解:(张三慧编著的大学物理学 P408)相干长度或波列长度是 m 23.0103.1103982=⨯⨯=∆=∆=νλλc L 相干时间是 s 107.7103.111109-⨯=⨯=∆==ντc L 2.19解:(张三慧编著的大学物理学 P408)地面上太阳光的空间相干间隔 μm 5510550200===-θλd (以双缝做实验,双缝的间距不能超过的距离) 2.20解:(钟锡华等光学习题解P125)设菲涅耳双面镜的夹角为02'=ε,缝光源S 离双面镜交线的距离为cm 10=l ,光源经双面镜 所成的两个虚像连线与接收屏幕平行,屏幕与双面镜交线的距离为cm 210='l ,光线波长nm 600=λ, 求干涉条纹的间距。
钟锡华P125由已知,cm D 220= cm l l d 116.0105402180060222=⨯=⨯''⨯==ππε mm d D x 14.1100.6116.02207=⨯⨯==∆-λ习题2.21解:(高教社题库)产生干涉允许的最大光程差就是光源的相干长度.光源的相干长度是 λλδΔ2=m而迈克耳孙测量中等效为薄膜干涉,由于厚度变化引起的光程差变化量是 d Δ2一次测量的量程m d Δ满足关系 λλδΔ2Δ2==m m d所以量程 λλδΔ22Δ2==mm d 由 λλδΔ22Δ2==mm d 计算镉谱线照射时一次测量的量程是 21cm m 21.010100.12108.643Δ22Δ9318212111==⨯⨯⨯⨯===---λλδm m d 计算氦氖激光照射时一次测量的量程是m 20010100.12108.632Δ22Δ9618222222=⨯⨯⨯⨯===---λλδm m d 计算表明,激光的相干长度长,所以一次测量的量程就长. 2.22解:(高教社题库)如图, 平行光垂直入射,经双棱镜 上下两半折射后,成为两束 倾角均为θ的相干平行光 (一束向上倾斜,另一束向 下倾斜).当幕与双棱镜的 距离大于或等于0L 时,两 束光在幕上的重叠区域为 零,干涉条纹数为零,最 少;当幕与双棱镜的距离 为图中的L 时,两束光在幕上的重叠区域为最大,干涉条纹数最多.利用折射定律求出倾角θ纹间距的公式及几何关系,即可求解.如图2,由折射定律 )s i n (s i n θαα+=n 采用小角近似,有 θαα+=n即 αθ)1(-=n式中α是双棱镜的顶角,θ是入射光束在双棱镜上、下两半折射后, 射出的两束相干平行光的倾角. 在幕上干涉条纹的间距为0.62mm m 102.618060π5.3)15.1(2106329)1(2sin 2sin 2Δ410=⨯=⨯⨯-⨯=-====--αλθλθλλn L L d D x 可见干涉条纹的间距与幕的位置无关.幕上可观察到的干涉条纹总数,由两束倾角均为θ的相干平行光(一束向上倾斜,另一束向下倾斜)在幕上重叠区的大小确定.如习题2.22图1,当幕与双棱镜的距离大于或等于0L 时,两束光在幕上的重叠区域为零,干涉条纹数为零.αθ)1(220-==n W W L m 3.3918060π5.3)15.1(2100.42=⨯⨯-⨯=- 当幕与双棱镜的距离为图中的L 时,两束光在幕上的重叠区域最大,干涉条纹数最多.m 6.192==L L 相应的重叠区域为0)1()1(22ΔL n L n L l ααθ-=-==m 02.03.3918060π5.3)15.1(=⨯⨯-=可看到的条纹数目是 条32102.602.0ΔΔ4=⨯=-x l 2.23解:(高教社题库)为了确定两相干光在幕上形成的干涉条纹的强度分布,关键在于两相干光在幕上任一点引起的振动的相位差.为此,适当选取坐标,根据题目给定的几何条件,写出两相干光在幕上任一点引起的振动的表达式即可求解.取直角坐标系xyz O -,屏幕在xy O -平面,z 轴沿两相干光束的角平分线. z y x ,,轴的单位矢量为k j,i,.则两束相干光在屏幕上任一点的振动为)c o s (111r k ⋅-=t E u ω)cos(222r k ⋅-=t E u ω式中 1:2:21=E E 是振动的振幅.而)2cos2sin(π21k i k θθλ+-=)2cos2(sinπ22k i k θθλ+=21,k k 是两束波的波矢, j i r y x += 是屏上任一点的位矢.故)2sinπ2cos(11x t E u ⋅+=θλω )2sinπ2cos(22x t E u ⋅-=θλω幕上两相干光的相位差为 x )2(s i n π4θλδ=屏幕上干涉强度的分布是 δcos 2212221E E E E I ++= 22221max 9)(E E E I =+= 22221min )(E E E I =-= 所以条纹的反衬度为 8.0108min max min max ==+-=I I I I γ极大值的位置满足下式 ,2,1,0π2)2(sin π4±±===k k x θλδ 相邻条纹的间距有关系π2Δ)2(sin π4=x θλ 得条纹间距 2s i n2Δθλ=x可见,当θ增大时,x Δ将减小,条纹变密. 2.24(高教社题库)平面波任意两点间的相位差与光程差的关系为 r k ΔΔ⋅=ϕ 其中k 是波矢量,大小为 λπ2=k , 方向就是波的传播方向. r Δ是两点间的位移.P 点的坐标和传播矢量k 的方向余弦分别是:λλλ36,3,10===z y x2330cos ,090cos ,2160cos o o o ===/6π/65-5习题2.25解答用图因此P 点的振动相位比坐标原点落后: )c o s c o s c o s (π2ΔΔγβαλϕz y x ++=⋅=r kπ28)32360210(π2=++=λλλ 2.25解:(高教社题库)四个无线电发射天线组成的天线阵列相当于四缝的多光束干涉.由题意知缝间距为2λ=d .相邻光束的光程差 θλθsin 2sin =d当 ),1,0(sin ±==k k d λθ 可能出现主极大的角位置 当 ),0(sin 的倍数的整数是N k Nk d ≠=λθ 可能出现极小的角位置由天线阵列主极大),1,0(s i n 2±==k k λθλ由于 1sin ≤θ 所以该阵列主极大只能有零级,即只能取 0=k 从而有0sin 2=θλ这样该天线阵列出现主极大的角位置只有 π,0==θθ 由极小光程差 ),0(sin 的倍数的整数是N k Nk d ≠=λθ 将 42==N d λ代入得),0(2sin 的倍数的整数是N k k ≠=θ因为 1sin ≤θ 只能取 2,1±±=k21sin 1±=±=θk 则 6π±=θ和 6π5±=θ1sin 2±=±=θk 则 2π±=θ结果是: 在 π,0==θθ 2个方向上强度最大(主极大);在 2π,6π5,6π±±±=θ 等6个方向上强度为零(极小). 干涉强度的角分布大致如下图所示. 计算表明,天线阵列的发射具有方向性,S在与阵列垂直方向上强度最大,其他方向都相当地弱. 2.26解:(高教社题库)恒星直接发射到射电望远镜的光与经湖面反射 后的光在射电望远镜处发生干涉,所以该题所设 装置就是一个劳埃德镜干涉装置.相干光路如图所示射光和反射光的几何程差是 BC AC - 考虑到光在湖面反射时有π的相位跃变, 所以两束光的光程差为2λ+-BC AC 由几何关系,得 ααα2c o s s i n s i n hh BC AC -=- αααααsin 2sin 2sin )2cos 1(sin 2h h h =⨯=-= 所以光程差为 2s i n2λα+h对于第1级极大有 λλα=+2s i n2h 解得恒星的角位置为 h4a r c s i n λα= 2.27解:(高教社题库)这是典型的分波前法获得相干光的装置.由透镜成像的基本原理可以知道,如果透镜未被切开时,在2f 处的点源S 应在透镜后2f 处成一实像点.现在,透镜的光心处在相距为h 的两点上,则点源由上半部透镜在2f 处成一实像点1S ,而又由下半部透镜在2f 处成一实像点2S ,则两实像点21,S S 就是两相干光源,相距为h d 2=, 相干光源距观察屏的距离是:f D 8= 相干光路如图。
