3第三章刚体的定轴转动解析
第三章 刚体的转动

M
o
r
F
M r F
m
力矩是矢量,M 的方向垂直于r和 F所决定的平面,其指向 用右手螺旋法则确定。
力矩的方向
2)力矩的单位、
牛· 米(N· m)
3)力矩的计算:
M 的大小、方向均与参考点的选择有关
M
m
M Fr sin
r
F
※在直角坐标系中,其表示式为 M r F ( xi yj zk ) ( Fx i Fy j Fz k )
例2 设质量为m,半径为R的细圆环和均匀圆盘分别绕通过各 自中心并与圆面垂直的轴转动,求圆环和圆盘的转动惯量.
解 (1)求质量为m,半径为R的圆环对中心轴的转动惯量.如图 (a)所示,在环上任取一质元,其质量为dm,该质元到转轴的距 离为R,则该质元对转轴的转动惯量为
dI R 2 dm
考虑到所有质元到转轴的距离均为R, 所以细圆环对中心轴的转动惯量为
dI x dm x dx
2 2
整个棒对中心轴的转 x dx ml 2 12
2
(2)转轴通过棒一端并与棒垂直时,整个棒对该轴的转动惯量为
1 2 I x dx ml 0 3
l 2
由此看出,同一均匀细棒,转轴位置不同,转动惯量不同.
刚体也是一个各质点之间无相对位置变化且质 量连续分布的质点系。
3.1 刚体定轴转动的描述
刚体的基本运动可以分为平动和转动,刚体 的各种复杂运动都可以看成是这两种运动的合成。
1.刚体的平动和定轴转动
平动
刚体的平动是指刚体在运动过 程中其中任意两点的连线始终保 持原来的方向(或者说,在运动 的各个时刻始终保持彼此平行)。 特点:其中各点在任意相同的时间内具有相同的位移和运动 轨迹,也具有相同的速度和加速度。因而刚体上任一点的运 动都可代表整个刚体的运动。 平动的刚体可看作质点。 刚体的转动比较复杂,我们只研究定轴转动。
刚体的定轴转动

J
1 2 m( R12 R2 ) 2
1 mR 2 2 若R1 R2 R, J mR 2
16
例:求长度为L,质量为m的均匀细棒AB的转动惯量。 (1)对于通过棒的一端与棒垂直的轴。 (2)对于通过棒的中心与棒垂直的轴。 m 解(1)细杆为线质量分布,单位长度的质量为: l L 1 3 2 2 dm A B J A x dm x dx L o 0 3 x
2 0
2
0
dm MR
2
绕圆环质心轴的转动惯量为
M
o
R
பைடு நூலகம்dm
J MR
2
讨论:若圆环绕其直径轴转动,再求此圆环的转动 惯量。
14
例: 一质量为m,半径为R的均匀圆盘,求对通过盘 中心并与盘面垂直的轴的转动惯量。
m 解: σ πR 2
dm σ 2π rdr
dJ r dm 2πσ r dr
5
匀变速圆周运动的基本公式
p
1 2 0 0t t 2
0 t
s
R
o
p
x
2 2 0 2 ( 0 )
定轴转动刚体上任一点的速度和加速度 s R 路程与角位移之间的关系:
v R 线速度与角速度的关系:
加速度与角量的关系: 2 dv d v at R R , an 2 R, dt dt R
1
柱壳形状的质元 ,其长为l半径为r厚度为dr, 则该质元的质量为 dm dV ( 2 rdr )l
R2
R2
l
J r dm 2lr dr
2 3 m R1
l
2
第三章刚体定点转动

第三章刚体定点转动§3.1定点转动运动学一、什么是定点转动?刚体转动时,如果刚体内只有一点始终保持不动,这种运动叫刚体的定点转动。
由于做定点转动时刚体上有一点固定不动,一般以定点为基点。
陀螺、回转罗盘(用于航空和航海方面)等,都是刚体绕定点转动的实例。
它们都只有一点不动。
如图3.1.1所示的常平架中的圆盘可绕对称轴z O ′转动,对称轴固结在内悬架上,内悬架可绕固结于外悬架的图3.1.1此,ON 轴转动而外悬架又可绕固定轴Oz 转动,此三轴的交点O 则是始终不动的,所以这种运动和定轴转动的情形不同。
二、定点转动和定轴转动的联系与区别1.联系:定点转动可以看成绕瞬时轴的定轴转动。
把某一瞬时角速度ω的取向,亦即在该瞬时的转动轴叫转动瞬轴。
跟转动瞬心相仿,转动瞬轴在空间和刚体内各描绘一个定点在O 的锥面,前者叫空间极面,后者则叫本体极面。
刚体绕固定点的转动,也可看作时本体极面在空间极面上作无滑动的滚动,如图3.1.2所示。
2.区别:(1)关于转轴:定点转动的轴恒通过一定点,但其在空间的取向随着时间的改变而改变,定轴转动的转轴在空间的取向不变。
(2)关于角速度:定点转动矢量的量值和方向都是时间的函数。
而定轴转动的角速度方向恒沿着固定的转动轴,量值可以是时间的函数。
ω三、定点转动时刚体上任一点的速度r dt r d v v vv ×==ωυ (3.1.1)P图3.1.3如图3.1.3所示,刚体上任一点P 的运动可以看成是绕瞬时轴的转动,所以其速度在圆周的切线方向,大小为R ωυ=.四、定点转动时刚体上任一点的加速度由加速度的定义知r r r dtd r r dt d r dt d dt d a vv v v v vv v v v v v v v v v v 2)()(ωωωωωωωυωωυ−⋅+×=××+×=×+×==而 R r r v v v v v 22)(ωωωω−=−⋅则R r dtd a v v v v 2ωω−×= (3.1.2)上式中的第一项r dtd vv×ω为转动加速度,第二项R v 2ω−为向轴加速度. 例:半径为a 的碾盘在水平面上做无滑滚动,长为b 的水平轴OA 绕竖直轴OE 以匀角速度1ω转动,如图3.1.4所示.求碾盘最高点P 的速度和加速度.x图3.1.4解: 碾盘绕定点O 运动,取如图所示的直角坐标系,OA=b,AB=OE=a,j a i b r P ˆˆ+−=v 要使碾盘在水平面上做无滑滚动,则瞬时角速度的方向为BO 方向,且iab j j i ˆˆˆˆ1121ωωωωω+=+=v.则 kb j a i b i ab j r P P ˆ2)ˆˆ()ˆˆ(111ωωωωυ=+−×+=×=vv v . 或用瞬轴法:P 点速度大小:b PD P 12ωωυ=⋅=. 方向:oz 轴方向.加速度: ja b i b r dt d dt d a P P Pˆˆ321221ωωυωωυ−=×+×==v v v v v v§3.2定点转动刚体对定点的动量矩一、刚体的动量矩图3.2.1刚体是一特殊的质点系,刚体作定点转动时对定点O 的动量矩(角动量)等于刚体上的各质点对定点O 的动量矩之和(矢量和)。
刚体的定轴转动

角速度是代数量,其正负表示刚体的转向。角速度为正值时表
明转角随时间而增加,刚体作逆时针转动;反之,转角随时间而减
小,刚体作顺时针转动。
角速度的单位是rad/s。工程上还常用每分钟转过的圈数表示刚
体转动的快慢,称为转速,用n表示,单位是r/min。角速度ω与转速
n之间的换算关系为
2n n
60 30
理论力学
刚体的运动\刚体的定轴转动
刚体的定轴转动
刚体运动时,若刚体内或其延伸部分有一直线始终保持不动, 刚体的这种运动称为定轴转动,简称转动。这条保持不动的直线称 为转轴。显然,刚体转动时,刚体内不在转轴上的各点都在垂直于 转轴的平面内作圆周运动,其圆心都在转轴上,圆的半径为该点到 转轴的垂直距离。
刚体的定轴转动在工程实际中随处可见,例如电动机转子的转 动,胶带轮、齿轮的转动等。
目录
刚体的运动\刚体的定轴转动
1.1 转动方程
设某刚体绕固定轴z转动,如图所示,为确定 该刚体在任一瞬时的位置,过转轴z作一固定平 面Ⅰ,再过转轴z作一与刚体固连、随刚体一起 转动的动平面Ⅱ。这样,该刚体在任一瞬时的位
置就可以用动平面Ⅱ与定平面Ⅰ的夹角确定, 角称为刚体的转角。当刚体转动时,转角是时
间t的单值连续函数,即 (t)
上式称为刚体的转动方程。若转动方程已知,则刚体在任一瞬时的 位置就确定了。因此,转动方程反映了刚体转动的规律。
转角是一个代数量,其正负号的规定如下:从转轴z的正端向 负端看去,逆时针转为正,反之为负。转角的单位是rad。
目录
刚体的运动\刚体的定轴转动
【例6.2】已知汽轮机在启动时主动轴的转动方程为t3,式中 的单位是rad,t的单位是s,求t=3s时该轴的角速度和角加速度。
刚体的定轴转动

第3章 刚体的定轴转动刚体定轴转动所遵从的力学规律,实际上是质点运动的基本概念和原理在刚体中的应用。
重要的概念有转动惯量和力矩。
刚体的动能和角动量都有其特殊的表达式,但守恒定律同样适用于包括刚体的系统。
§1 刚体的运动一 刚体刚体是固体物件的理想化模型。
实际的固体在受力作用时总是要发生或大或小的形状和体积的改变。
如果在讨论一个固体的运动时,这种形状或体积的改变可以忽略,我们就把这个固体当做刚体处理。
这就是说,刚体是受力时不改变形状和体积的物体。
刚体可以看成由许多质点组成,每一个质点叫做刚体的一个质元,刚体这个质点系的特点是,在外力作用下各质元之间的相对位置保持不变。
既然是一个质点系。
所以关于质点系的基本定律就都可以应用。
当然,由于刚体这一质点系有其特点,所以这些基本定律就表现为更适合于研究刚体运动的特殊形式。
二 刚体的运动形式刚体的运动可以是平动、转动或二者的结合。
如果刚体在运动中,连结体内两点的直线在空间的指向总保持平行,这样的运动就叫平动。
在平动时,刚体内各质元的运动轨迹都一样,而且在同一时刻的速度和加速度都相等。
因此在描述刚体的平动时,就可以用一点的运动来代表,通常就用刚体质心的运动来代表整个刚体的平动。
平动是刚体的基本运动形式之一。
转动也是刚体的基本运动形式之一,它又可分为定轴转动和定点转动。
定轴转动:运动中各质元均做圆周运动,且各圆心都在同一条固定的直线(转轴)上。
定点转动:运动中刚体上只有一点固定不动,整个刚体绕过该定点的某一瞬时轴线转动。
刚体不受任何限制的的任意运动。
它可分解为以下两种刚体的基本运动:随基点(可任选)的平动,绕通过基点的瞬时轴的定点转动。
三 刚体定轴转动的运动学描述刚体的定轴转动是最简单的转动情况。
在这种运动中各质元均做圆周运动,而且各圆的圆心都在一条固定不动的直线上,这条直线叫转轴。
刚体绕某一固定转轴转动时,各质元作圆周运动的轨道半径不同,所以各质元的线速度、加速度一般是不同的。
力学讲义-3刚体的定轴转动

物体(包括子弹)在 B 点的速度大小和θ 角的大小。
【思路分析】 此题可分两个过程,第一阶段,子弹射入木块前后,水平方向动量守恒;
第二阶段,含子弹的木块由 A 点沿曲线运动到 B 点,由于作用在木块上的弹簧拉力为有心
力,所以角动量守恒。同时,机械能也守恒,可解之。
解 子弹与木块作完全非弹性碰撞,水平方向动量守恒。设碰后的速度为 uK ,其大小为
(1)
T2 − m2 g sin α = m2a
(2)
另根据转动定律,对滑轮有
还有辅助方程
T1′R − T2′R = J β
T1′ = T1 T2′ = T2 a = Rβ
联立求解上述六个方程,解得 m1 的加速度大小为
a
=
(
m1 − m2 sinα (m1 + m2 )R2
) gR2
+J
(3)
(4) (5) (6)
与质点直线运动相对应的定理和定律,为便于记忆和理解,此处给出了质点一维运动与刚体
定轴转动的相应公式:
2
质点一维运动
刚体定轴转动
位移 Δx 速度 υ = dx
dt
加速度 a = dυ = d2 x dt dt2
质量 m
K 力F
运动定律
K F
=
maK
动量
K P
=
mυK
动量定理
JK dp
=
JK F
dt
∫K Fdt
向弹回,碰撞时间极短,如图 3-4 所示。已知滑块与棒碰撞
前后的速率分别为υ 和 u ,桌面与细棒间的滑动摩擦系数为 μ 。求从碰撞后到细棒停止运动所需的时间。
【思路分析】 首先由碰撞过程角动量守恒求出碰后细棒的角速度,再求得细棒受到的
大学物理同步训练第2版第三章刚体定轴转动详解

mg
3g 1 cos L 1 1 1 cos mL2 2 2 2 3 L
可知当 从 0 至 90 度的过程中,角速度从小到大。 5. (☆)如图 3 所示,A、B 为两个相同的绕着轻绳的定滑轮。A 滑 轮挂一质量为 m 的物体,B 滑轮受拉力 G,而且 G=mg。设 A、B 两 滑轮的角加速度分别为βA 和βB,不计滑轮轴的摩擦,则有 (A) A B (C) A B 答案:C 分析: (定性)由于物体 m 有向下的加速度,故作用于物体上的绳子张力小于 mg,即小于 右边绳子的张力(=mg) ,故 A 滑轮受到的力矩小于 B 滑轮,故 A B 。 (定量)设圆盘转动惯量为 I ,参考计算题第 1 题的计算过程,可得 A、B 圆盘的转动角加 速度为 (B) A B (D)开始时 A B ,以后 A B
mg TA ma mgR mgR A ; GR I B B TA R I A 2 I mR I R a A
故 A B 。 6. 一轻绳跨过一具有水平光滑轴、转动惯量为 J 的定滑轮, 绳的两端分别悬 有质量为 m1 和 m2 的物体 (m1<m2) , 如图 4 所示。 绳与轮之间无相对滑动。 若某时刻滑轮沿逆时针方向转动,则绳中的张力 (A)处处相等 (C)右边大于左边 答案:C 分析: (定性)由于重的物体 m2 最终必然下落,可知圆盘最后将做顺时针转动,因此圆盘 受到的合外力矩应为顺时针,即右边绳子的张力要大于左边绳子的张力。 (定量)参考课本例题( (★)阿特伍德机:P84,例 3-5)可得 (B)左边大于右边 (D)无法判断哪边大
A J B A
6. (☆)如图 10 所示,一静止的均匀细棒,长为 L,质量为 m1,可绕通过棒的端点且垂直 于棒长的光滑固定轴 O 在水平面内转动,转动惯量为 m1L2/3。一质量为 m、速率为 v 的子 弹在水平面内沿与棒垂直的方向射出并穿出棒的自由端,设穿过棒后子弹的速率为 v/2,则 此时棒的角速度应为 答案: 。
第3章 刚体的定轴转动
F
Od
r *ϕ
P
方向: 沿轴向(使刚体绕轴逆时针改变运动状态为正) 方向: 沿轴向(使刚体绕轴逆时针改变运动状态为正) 单位: 单位: N ⋅ m (牛⋅米) 定轴转动的刚体受到几个力矩的作用, 定轴转动的刚体受到几个力矩的作用,合力矩是 各力矩的代数和。 各力矩的代数和。
6
3.2 刚体的定轴转动定律
4
3.1 刚体的运动
当刚体绕定轴转动的角加速度为恒量时, 当刚体绕定轴转动的角加速度为恒量时,刚体作 匀变速转动 。 刚体匀变速转动与质点匀变速直线运动公式对比 质点匀变速直线运动 质点匀变速直线运动 刚体绕 刚体绕定轴作匀变速转动
v = v 0 + at
x = x 0 + v 0 t + at
1 2
1
3.1 刚体的运动
3.1.2 刚体的定轴转动
转动:组成刚体的各质点都绕某一直线作 组成刚体的各质点都绕某一直线作 圆周运动, 这条线为转轴。 圆周运动, 这条线为转轴。 转轴 若转轴相对于给定的参考系在空间 固定不动,则称为刚体的定轴转动。 固定不动,则称为刚体的定轴转动。 刚体的定轴转动 刚体的一般运动 (如:运行的车轮) 运行的车轮) 随某点(基点) 随某点(基点)的平动 + 过该点 的定轴转动。 的定轴转动。
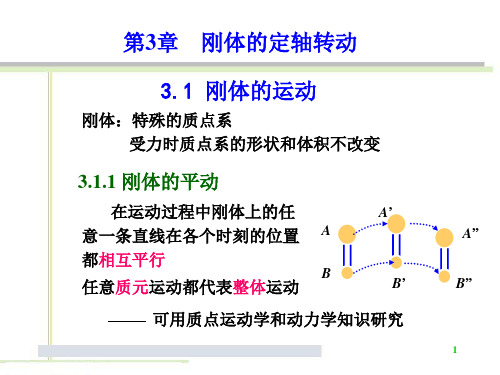
第3章 刚体的定轴转动 章 3.1 刚体的运动
刚体: 刚体:特殊的质点系 受力时质点系的形状和体积不改变
3.1.1 刚体的平动
在运动过程中刚体上的任 意一条直线在各个时刻的位置 都相互平行 任意质元运动都代表整体运动 任意质元运动都代表整体运动 质元运动都代表整体
A’ A B A”
B’
B”
可用质点运动学和动力学知识研究
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)
碰前
O O
1 m( 2L )2 12
u m v m
因作弹性碰撞,故在碰撞过程 中动能守恒 :
碰后
1 mu2 1 mv 2 1 J 2 ( 2 ) 2 2 2 m 3 m u 由(1) (2)解得: v m 3m
J
6 m u ( m 3m ) L
小结:弹性碰撞: 质点→动能守恒、动量守恒。 动量守恒? 刚体→动能守恒、角动量守恒;
否
例2 一杂技演员 M 由距水平跷板高为 h 处自由下落到跷板 的一端A,并把跷板另一端的演员N 弹了起来.设跷板是匀质的,长度 为l,质量为 m',跷板可绕中部支撑点C 在竖直平面内转动,演员的质 量均为m.假定演员M落在跷板上,与跷板的碰撞是完全非弹性碰撞. 问演员N可弹起多高?
解:受力分析:
在非惯性系中牛顿第二定律形式,
m1 gj Tj m1aj m1ar j m2 gj Tj m2aj m2 (ar j )
完全非弹性碰撞? 动能损失最大,演员M、N和翘班具有相同速率
碰撞过程冲量矩=? 解 碰撞前 M 落在 A点 的速度
M的重力冲量矩可忽略
vM ( 2gh )1 2
u2 h 2g
M
碰撞后的瞬间, 考虑非弹 性碰撞,M、N具有相同 的角速度, 故其线速度为
h
C A l/2
N B
l u 2
l
演员 N 以 u 起跳, 达到的高度
u2 l 2 2 3m h ( )2 h 8g m 6m 2g
§ 5 —6
进动 (Precession)
1.进动:陀螺在绕本身的对称轴线转动的同时,对称轴还将绕竖 直轴 OZ 转动,这种回转现象称为进动。 2.进动产生的原因:
重力对 0 点的力矩为 M , M 的方向: r mg
力矩或冲量矩为零 角动量守恒 只有保守力矩做功
机械能守恒
1、无守恒量,则考虑: 角动量定理或定轴转动定律
例1.匀质细棒质量为m,长为2L,可在铅直平面内绕通过其中心 的水平轴O自由转动. 开始时棒静止于水平位置,一质量为m' 的小球,以速度u垂直落到棒的端点,且与棒作弹性碰撞.求:碰 撞后小球的回跳速度以及棒的角速度. 什么是弹性碰撞? 动能损失为零,动能守恒。 若为质点则动能守恒、动量守恒; 在碰撞过程中, 外力矩=? 小球的重力矩mgL
习题课1-3章 作业:第三章剩余部分 本周四交齐!
答疑时间、地点:
单周一、双周二 双周三、单周四 东九楼A210室 西五楼116室
晚上7:30—9:30
课本81页 dA F dr F cos dr 改为: dA F dr F cos dr
律
律
•转动惯量的计算
(1) 求通过质心的转动惯量 JC r 2 dm r 2 dV M M (2) 求任一平行质心转轴的转动惯量
根据角动量定理: Mdt dL dL 的方向与 M 一致
Z
p
L dL
dL
L
ML
dL L
即 dL始终与角动量 L 垂直
重力矩只改变 L 方向 大小不变
(类比:当向心力始终与质点速度垂 直,只改变速度方向不改变大小)
0 mg
故陀螺的自转轴改变方向,绕一 竖直轴进动
d 进动的角速度: p dt
d dS / L sin
dS dL
L sin
p d
L sin L
dL
dL M d t d
dL Mdt
r
O
mg
d M p dt L sin M p M L sin J sin
进动角速度与自旋角速度成反比 只考虑重力矩 M r mg rmg sin
解: 以棒和小球为系统. 在碰撞过程中, 对轴O的外力矩只 有小球的重力矩mgL . 因碰撞时间极短, 冲量矩可忽略。
O u Mdt dL 0 ? m 系统对转轴O的角动量守恒:
碰前
mg
O
v m
L0 Lt
muL J mvL
(1)
碰后
muL J mvL
v2 135 j
v1 135sin30 i 135cos 30 j
o o
u 135sin30o i 135(1 cos 30o ) j
67.5i 18.09 j
o tan 75 u 69.9km / h
2-T5 如图所示,一根绳子跨过电梯内的定滑轮,其两端旋挂 质量不等的物体,m1>m2,滑轮和绳子质量忽略。求当电梯以 加速度a上升时,绳子的张力T和质量为m1的物体相对电梯的 加速度ar。 非惯性系问题 a
M
2
利用平行轴定理
J=JC+md
•刚体的角动量定理 t Mdt J J 00
0
•刚体的角动量守恒
当合外力矩
M 0
J
常数
自然界中存在多种守恒定律
动量守恒定律 能量守恒定律 角动量守恒定律 刚体动力学解题思路:
1、判断是否有守恒量
电荷守恒定律 质量守恒定律 宇称守恒定律等
l u 2
下面求ω=? 把M、N和跷板作为一 个系统, 角动量守恒
பைடு நூலகம்
M
h N
B l C l/2 A
l l m vM J 2mu 1 ml 2 1 ml 2 2 12 2 2 m vM l 2 6m( 2gh )1 2 解得 2 2 ml 12 ml 2 ( m 6m )l
1-T4 一架飞机在静止空气中的速度v1=135km/h。在刮风天气,飞 机以v2=135km/h的速率向正北方向飞行,机头指向北偏东30o。请 协助驾驶员判断风向和风速。
j
解:v2: 绝对速度
v1: 相对速度
v绝对 v相对 v牵连
求牵连速度? u
v2
u
v1
i
据v2 v1 u
讨论:
p
可否θ增加,
p ?
进动的应用举例:
(1) 枪弹、炮弹在飞行时能绕自身 的质心旋转,在空气阻力的作用 下翻“筋斗”; 来复线使其产生进动,使运动基 本保持原方向。
M
p
vC
f
(2)*原子中电子除绕原子核转动外, 在外磁场中的进动(拉莫进动)
M pm B
习题解答:
v绝对 v相对 v牵连
